The half-life or radioactive period of a radioactive isotope is the time required for half of the nuclei in a sample to decay. It is a characteristic quantity of an unstable nucleus and a probabilistic measure of its stability. The half-life is independent of the amount of material or external conditions (temperature, pressure, etc.) because radioactive decay is a purely quantum process, governed by the laws of quantum mechanics.
A short half-life means rapid decay (very unstable element). A long half-life indicates a more stable element.
No, not all chemical elements have a measurable half-life, because some isotopes are stable. For example, carbon-12 (12C), oxygen-16 (16O), or iron-56 (56Fe) do not decay spontaneously, even over timescales comparable to the age of the Universe. On the other hand, radioactive elements such as uranium, thorium, or polonium have one or more unstable forms (isotopes) with half-lives ranging from microseconds to billions of years.
The radioactive period, often denoted \( T_{1/2} \), of a chemical element (or more precisely of a radioactive nuclide) is thus the time required for half of the nuclei in a given sample to decay spontaneously. It is a measure of nuclear stability.
For a sample containing \( N_0 \) nuclei at time \( t = 0 \), the radioactive decay law is: \( N(t) = N_0 \cdot e^{-\lambda t} \)
The half-life \( T_{1/2} \) is related to \( \lambda \) by: \( T_{1/2} = \frac{\ln(2)}{\lambda} \)
| Element | Isotope | Half-Life (seconds) | Half-Life (Readable Form) |
|---|---|---|---|
| Polonium | Po-212 | 0.0000003 | 0.3 µs |
| Livermorium | Lv-293 | 0.061 | 61 ms |
| Californium | Cf-251 | 0.9 | 0.9 s |
| Francium | Fr-223 | 1320 | 22 min |
| Technetium | Tc-99m | 21600 | 6 h |
| Iodine | I-131 | 693,728 | 8.02 d |
| Cobalt | Co-60 | 166,824,000 | 5.27 years |
| Hydrogen | Tritium | 388,435,680 | 12.32 years |
| Carbon | C-14 | 180,622,080,000 | 5730 years |
| Plutonium | Pu-239 | 760,585,760,000 | 24,100 years |
| Uranium | U-234 | 7,740,138,000,000 | 245,500 years |
| Uranium | U-235 | 22,174,070,000,000 | 703 million years |
| Uranium | U-238 | 141,379,620,000,000 | 4.468 billion years |
| Thorium | Th-232 | 443,538,150,000,000 | 14.05 billion years |
| Tellurium | Te-128 | 6.945×10²⁴ | 2.2×10²⁴ s (~7×10¹⁶ years) |
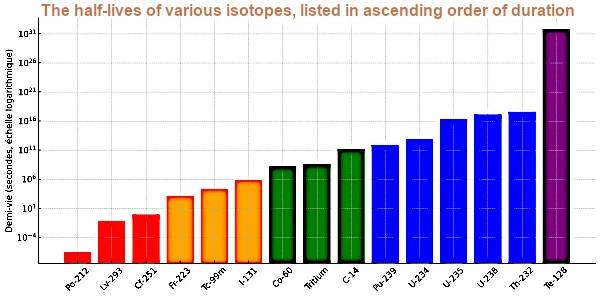
This graph shows the half-lives of selected isotopes, ranked in increasing order. The logarithmic scale allows visualization of the enormous differences, ranging from microseconds to more than 10²⁴ seconds.