L’atome sous toutes ses formes: de l’intuition antique à la mécanique quantique

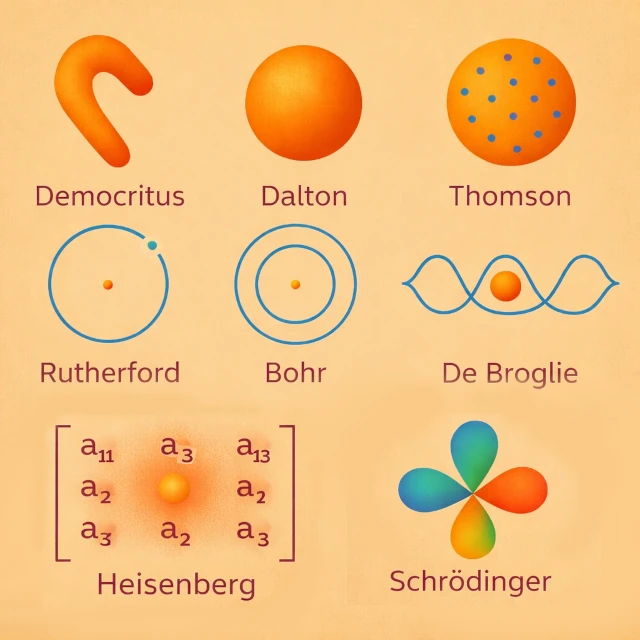
Évolution historique des modélisations de l’atome — Représentation schématique de l’évolution des modélisations atomiques, depuis l’atome indivisible jusqu’aux orbitales quantiques.
Source image : astronoo.com (nouvelle fenêtre).

Résumé scientifique

L'article retrace l'évolution de la modélisation de l'atome, des intuitions philosophiques de Démocrite (atome indivisible) à la mécanique quantique probabiliste. Cette révolution scientifique passe par les modèles clés : Dalton (atome chimique sphérique), Thomson (électrons dispersés dans une sphère positive), Rutherford (noyau central compact), Bohr (orbites quantifiées), de Broglie (dualité onde-particule), Heisenberg (principe d'incertitude, trajectoires indéterminées) et Schrödinger (nuages de probabilité, fonction d'onde). Chaque modèle corrige les limites du précédent, reflétant l'évolution de la physique classique vers la physique quantique, où l'électron n'a plus de trajectoire définie mais une probabilité de présence décrite par des orbitales atomiques.

Comment la modélisation de l'atome a-t-elle évolué au cours de l'histoire des sciences ?

La représentation de l'atome a connu une révolution scientifique majeure, passant d'un concept philosophique à un modèle quantique probabiliste. L'évolution commence avec Démocrite (atome indivisible), puis Dalton (atome chimique sphérique), Thomson (modèle « plum pudding » avec électrons dispersés), Rutherford (noyau central compact), Bohr (orbites quantifiées), de Broglie (dualité onde-particule, ondes stationnaires), Heisenberg (mécanique matricielle, principe d'incertitude) et Schrödinger (nuages de probabilité, fonction d'onde). Cette succession de modèles reflète l'évolution de la physique, de la mécanique classique à la mécanique quantique, où l'électron n'a plus de trajectoire définie mais une probabilité de présence.

À découvrir aussi

Poursuivez votre exploration de l'Univers avec ces sujets :

Aux origines philosophiques de l’atome

Le concept d’atome apparaît au 5e siècle BCE avec Démocrite (vers 460-370 BCE), qui postule, par une démarche essentiellement intuitive et rationnelle, l’existence de particules indivisibles se déplaçant dans le vide. Cette proposition ne repose pas sur l’observation expérimentale, mais sur une intuition philosophique visant à résoudre le problème de la divisibilité infinie de la matière. Aucune expérience ne permet alors de tester cette hypothèse. L’atome est ainsi pensé comme une unité ultime de la matière, sans structure interne ni propriétés mesurables. Pour Démocrite l'atome possède une forme propre qui explique intuitivement les propriétés des corps: par exemple, des atomes crochus s’imbriquent et donnent des textures rugueuses, tandis que des atomes ronds ou lisses produisent des substances fluides ou douces.

Le Moyen Âge: entre continuité aristotélicienne et atomisme théologique

Au Moyen Âge, il n’existe pas de modélisation physique de l’atome au sens scientifique, car la pensée naturelle européenne est largement dominée par l’héritage d’Aristote, pour qui la matière est continue, indéfiniment divisible, et structurée par les quatre éléments (la terre, l'eau, l'air et le feu). Cette vision exclut l’existence d’unités matérielles indivisibles et s’oppose explicitement à l’atomisme antique. Toutefois, dans le monde islamique médiéval, certains courants de la théologie rationnelle, notamment le kalām, développent une forme d’atomisme philosophique dans laquelle le monde est composé d’atomes discrets recréés à chaque instant par la volonté divine. Cet atomisme médiéval ne repose ni sur l’expérience ni sur des lois mathématiques, mais sur une intuition métaphysique visant à concilier causalité, contingence et toute-puissance divine. Ainsi, durant le Moyen Âge, l’atome subsiste comme concept spéculatif ou théologique, sans devenir un objet de description physique ou de mesure.

La naissance de l’atome scientifique

Au début du 19e siècle CE, John Dalton (1766-1844) introduit une théorie atomique fondée sur la chimie quantitative. Les atomes deviennent des entités chimiques et mesurables, caractérisées par leur masse, et responsables des lois de conservation. Chaque élément chimique est constitué d’atomes identiques, distincts de ceux des autres éléments. Par exemple, dans la formation de l’eau, Dalton explique que chaque molécule résulte de la combinaison de deux atomes d’hydrogène et d’un atome d’oxygène (H₂O), conformément à des proportions simples et constantes. Cette observation expérimentale illustre comment les atomes gouvernent les réactions chimiques et leurs proportions. Visuellement, on peut imaginer que Dalton pensait l’atome comme une sphère compacte et homogène, sans structure interne, juste comme “une petite bille de matière”.

Le modèle de Thomson: l’atome "plum pudding"

La fin du 19e siècle CE marque une rupture décisive dans la conception de l’atome. En 1897, Joseph John Thomson (1856-1940) découvre l’électron, démontrant que l’atome n’est pas indivisible. Il propose alors un modèle où les électrons, porteurs de charge négative, sont dispersés dans une sphère de charge positive diffuse, comme des raisins dans un pudding. Ce modèle permet d’expliquer certaines propriétés électriques des atomes, mais ne rend pas compte de la stabilité du noyau observée plus tard.

Le modèle de Rutherford: l’atome nucléaire

En 1911, Ernest Rutherford (1871-1937) interprète l’expérience de diffusion des particules alpha. Il démontre que la charge positive et l’essentiel de la masse de l’atome sont concentrés dans un noyau central compact. Les électrons gravitent autour de ce noyau, et l’atome devient un système majoritairement constitué de vide. Ce modèle corrige les limites du modèle de Thomson et pose les bases des développements quantiques ultérieurs.

Le modèle de Niels Bohr: Quantification de l’atome

Le modèle planétaire classique est instable selon l’électromagnétisme car, en physique classique, une charge accélérée comme un électron en orbite rayonne de l’énergie électromagnétique, perd progressivement son énergie cinétique et spirale inévitablement vers le noyau. Pour résoudre cette contradiction, Niels Bohr (1885-1962) introduit en 1913 des orbites électroniques quantifiées. Les électrons ne peuvent occuper que certains niveaux d’énergie, expliquant les spectres atomiques discrets.

Le modèle ondulatoire de Louis de Broglie: Onde stationnaire

Au début du 20e siècle CE, Louis de Broglie (1892-1987) propose une révolution conceptuelle: l’électron, et plus généralement toute particule matérielle, possède à la fois une nature "corpuscule" et une nature "onde". Cette idée, appelée dualité onde-corpuscule, suggère que l’électron en orbite autour du noyau peut être décrit comme une "onde stationnaire", dont la longueur d’onde est inversement proportionnelle à sa quantité de mouvement: \( \lambda = h / p \), où \( \lambda \) est la longueur d’onde, \( h \) la constante de Planck, et \( p \) la quantité de mouvement.

Le modèle de de Broglie explique pourquoi seules certaines orbites sont stables dans l’atome de Bohr: l’électron ne peut occuper que les orbites pour lesquelles sa longueur d’onde forme un cycle complet autour du noyau, créant une condition de résonance. Ce concept constitue une étape essentielle vers la "mécanique quantique", car il relie les propriétés corpusculaires des particules à leur comportement ondulatoire, ouvrant la voie à l’équation de Schrödinger.

Le modèle de Heisenberg: Mécanique quantique matricielle

Dans les années 1920 CE, Werner Heisenberg (1901-1976) propose une nouvelle approche de l’atome fondée sur les principes de la mécanique quantique. Son modèle, dit "mécanique quantique matricielle", ne cherche pas à décrire la trajectoire des électrons autour du noyau, mais uniquement les "valeurs observables" telles que les énergies des niveaux atomiques et les probabilités de transition entre eux. Heisenberg introduit le célèbre "principe d’incertitude", qui stipule qu’il est impossible de connaître simultanément et avec précision la position et la quantité de mouvement d’un électron (\( \Delta x \, \Delta p \ge \hbar / 2 \)).

Ce modèle transforme radicalement la compréhension de l’atome: les électrons ne sont plus vus comme des particules décrites par des orbites classiques, mais comme des entités dont le comportement ne peut être exprimé que par des grandeurs mesurables. Le modèle de Heisenberg est très abstrait et ne se prête pas à une illustration classique d’électrons en orbite, contrairement à Bohr. Mais on peut quand même le représenter de manière symbolique et pédagogique.

Le modèle quantique de Schrödinger: Des nuages de probabilité

Au début des années 1920 CE, la physique classique ne peut plus expliquer la stabilité des atomes ni les spectres discrets observés expérimentalement. Erwin Schrödinger (1887-1961) développe alors une approche mathématique fondée sur la mécanique ondulatoire. Il remplace les trajectoires électroniques fixes par une fonction d’onde (fonction mathématique solution de l’équation de Schrödinger représentant la probabilité de présence de l’électron), dont le carré du module indique la probabilité de présence de l’électron dans l’espace.

Cette approche décrit les électrons comme des "nuages de probabilité" organisés en orbitales atomiques (régions de l’espace où la probabilité de présence de l’électron est significative), caractérisées par des nombres quantiques définissant énergie, forme et orientation. Le modèle de Schrödinger rend compte de la stabilité des atomes, des spectres atomiques et sert de fondement à toute la chimie quantique moderne.

N.B. :
Contrairement aux modèles classiques, l’électron n’a pas de trajectoire définie. La mécanique quantique ne décrit que des probabilités de présence et d’énergie.

Comparaison des principales modélisations atomiques

Évolution des modélisations physiques de l’atome
Modélisation	Scientifique	Période	Caractéristique principale
Atome indivisible	Démocrite (vers 460-370 BCE)	5e siècle BCE	Particule sans structure interne
Atome chimique	John Dalton (1766-1844)	19e siècle CE	Masse définie, base des réactions chimiques
Modélisation de Thomson	Joseph John Thomson (1856-1940)	Fin 19e siècle CE	Électrons plongés dans une charge positive diffuse
Modélisation nucléaire	Ernest Rutherford (1871-1937)	Début 20e siècle CE	Noyau central et électrons périphériques
Modélisation quantifiée	Niels Bohr (1885-1962)	Début 20e siècle CE	Niveaux d’énergie discrets
Modélisation ondulatoire	Louis de Broglie (1892-1987)	20e siècle CE	Dualité onde-particule appliquée à l’électron
Modélisation matricielle	Werner Heisenberg (1901-1976)	20e siècle CE	Grandeurs observables, principe d’incertitude, trajectoires indéterminées
Modélisation quantique	Erwin Schrödinger (1887-1961)	20e siècle CE	Fonction d’onde et orbitales de probabilité

FAQ : Tout savoir sur les modélisations de l'atome

Pourquoi le modèle de Rutherford a-t-il remplacé celui de Thomson ?

Le modèle de Thomson (« plum pudding ») proposait que les électrons négatifs soient dispersés dans une sphère de charge positive diffuse. En 1911, Rutherford réalisa une expérience de diffusion de particules alpha sur une fine feuille d'or. Il observa que certaines particules étaient rétrodiffusées, ce qui prouvait la présence d'un noyau central compact et massif, concentrant l'essentiel de la masse et toute la charge positive de l'atome. Le modèle de Thomson ne pouvait pas expliquer ces résultats, tandis que le modèle nucléaire de Rutherford le pouvait.

Quelle est la différence fondamentale entre le modèle de Bohr et le modèle de Schrödinger ?

Le modèle de Bohr (1913) proposait des orbites électroniques circulaires quantifiées, comme des planètes autour du Soleil, mais avec des niveaux d'énergie discrets. Le modèle de Schrödinger (années 1920) a remplacé ces orbites fixes par une fonction d'onde dont le carré du module donne la probabilité de présence de l'électron. L'électron n'a donc plus de trajectoire définie, mais forme des « nuages de probabilité » appelés orbitales atomiques. Le modèle de Schrödinger est plus précis et sert de fondement à la chimie quantique moderne.

Qu'est-ce que la dualité onde-particule et quel est son apport à la modélisation de l'atome ?

Proposée par Louis de Broglie au début du 20e siècle, la dualité onde-particule énonce que toute particule matérielle (comme l'électron) possède à la fois une nature corpusculaire et une nature ondulatoire, avec une longueur d'onde associée λ = h/p (où h est la constante de Planck et p la quantité de mouvement). Appliquée à l'atome, cette idée explique pourquoi seules certaines orbites sont stables dans le modèle de Bohr : l'électron ne peut occuper que les orbites pour lesquelles sa longueur d'onde forme un cycle complet autour du noyau (condition de résonance). Ce concept a ouvert la voie à l'équation de Schrödinger et à la mécanique quantique.