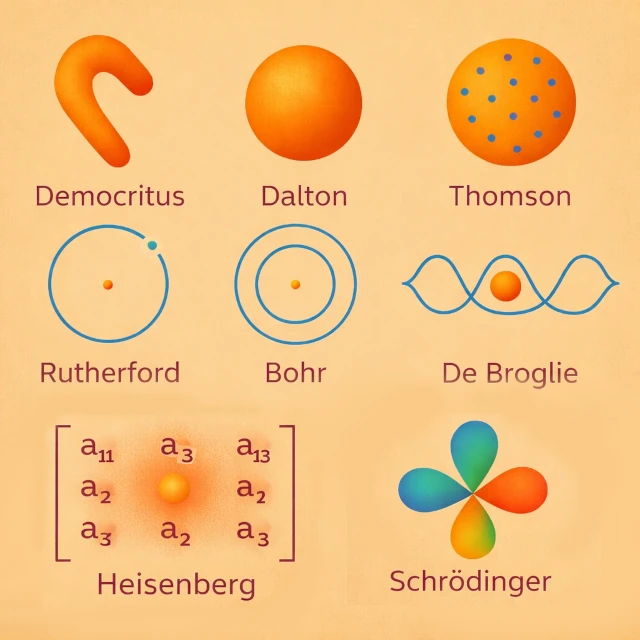
El concepto de átomo apareció en el siglo V a.C. con Demócrito (c. 460-370 a.C.), quien postuló, mediante un enfoque esencialmente intuitivo y racional, la existencia de partículas indivisibles que se mueven en el vacío. Esta propuesta no se basaba en la observación experimental, sino en una intuición filosófica destinada a resolver el problema de la divisibilidad infinita de la materia. Ningún experimento podía probar entonces esta hipótesis. El átomo se concebía así como la unidad última de la materia, sin estructura interna ni propiedades medibles. Para Demócrito, el átomo tenía una forma propia que explicaba intuitivamente las propiedades de los cuerpos: por ejemplo, los átomos con ganchos se entrelazaban y daban texturas ásperas, mientras que los átomos redondos o lisos producían sustancias fluidas o suaves.
En la Edad Media, no existía una modelización física del átomo en el sentido científico, ya que el pensamiento natural europeo estaba ampliamente dominado por el legado de Aristóteles, para quien la materia es continua, infinitamente divisible y estructurada por los cuatro elementos (tierra, agua, aire y fuego). Esta visión excluía la existencia de unidades materiales indivisibles y se oponía explícitamente al atomismo antiguo. Sin embargo, en el mundo islámico medieval, algunas corrientes de la teología racional, en particular el kalām, desarrollaron una forma de atomismo filosófico en la que el mundo estaba compuesto por átomos discretos recreados en cada instante por la voluntad divina. Este atomismo medieval no se basaba ni en la experiencia ni en leyes matemáticas, sino en una intuición metafísica destinada a conciliar la causalidad, la contingencia y la omnipotencia divina. Así, durante la Edad Media, el átomo persistió como un concepto especulativo o teológico, sin convertirse en un objeto de descripción física o de medición.
A principios del siglo XIX d.C., John Dalton (1766-1844) introdujo una teoría atómica basada en la química cuantitativa. Los átomos se convirtieron en entidades químicas y medibles, caracterizadas por su masa, y responsables de las leyes de conservación. Cada elemento químico está compuesto por átomos idénticos, distintos de los de otros elementos. Por ejemplo, en la formación del agua, Dalton explicó que cada molécula resulta de la combinación de dos átomos de hidrógeno y un átomo de oxígeno (H₂O), de acuerdo con proporciones simples y constantes. Esta observación experimental ilustra cómo los átomos gobiernan las reacciones químicas y sus proporciones. Visualmente, se puede imaginar que Dalton pensaba en el átomo como una esfera compacta y homogénea, sin estructura interna, simplemente como "una pequeña bola de materia".
A finales del siglo XIX d.C., se produjo una ruptura decisiva en la concepción del átomo. En 1897, Joseph John Thomson (1856-1940) descubrió el electrón, demostrando que el átomo no es indivisible. Propuso entonces un modelo en el que los electrones, portadores de carga negativa, están dispersos en una esfera de carga positiva difusa, como pasas en un pudín. Este modelo permitía explicar ciertas propiedades eléctricas de los átomos, pero no explicaba la estabilidad del núcleo observada más tarde.
En 1911, Ernest Rutherford (1871-1937) interpretó el experimento de dispersión de partículas alfa. Demostró que la carga positiva y la mayor parte de la masa del átomo están concentradas en un núcleo central compacto. Los electrones giran alrededor de este núcleo, y el átomo se convierte en un sistema compuesto principalmente de vacío. Este modelo corrigió las limitaciones del modelo de Thomson y sentó las bases para los desarrollos cuánticos posteriores.
El modelo planetario clásico es inestable según el electromagnetismo, porque en la física clásica, una carga acelerada como un electrón en órbita irradia energía electromagnética, pierde gradualmente su energía cinética y espirala inevitablemente hacia el núcleo. Para resolver esta contradicción, Niels Bohr (1885-1962) introdujo en 1913 órbitas electrónicas cuantificadas. Los electrones solo pueden ocupar ciertos niveles de energía, lo que explica los espectros atómicos discretos.
A principios del siglo XX d.C., Louis de Broglie (1892-1987) propuso una revolución conceptual: el electrón, y en general cualquier partícula material, tiene tanto una naturaleza de "partícula" como de "onda". Esta idea, llamada dualidad onda-partícula, sugiere que el electrón en órbita alrededor del núcleo puede describirse como una "onda estacionaria", cuya longitud de onda es inversamente proporcional a su cantidad de movimiento: \( \lambda = h / p \), donde \( \lambda \) es la longitud de onda, \( h \) es la constante de Planck y \( p \) es la cantidad de movimiento.
El modelo de de Broglie explica por qué solo ciertas órbitas son estables en el átomo de Bohr: el electrón solo puede ocupar las órbitas para las cuales su longitud de onda forma un ciclo completo alrededor del núcleo, creando una condición de resonancia. Este concepto constituyó un paso esencial hacia la "mecánica cuántica", ya que relacionó las propiedades corpusculares de las partículas con su comportamiento ondulatorio, allanando el camino para la ecuación de Schrödinger.
En la década de 1920 d.C., Werner Heisenberg (1901-1976) propuso un nuevo enfoque del átomo basado en los principios de la mecánica cuántica. Su modelo, llamado "mecánica cuántica matricial", no buscaba describir la trayectoria de los electrones alrededor del núcleo, sino solo las "cantidades observables" como las energías de los niveles atómicos y las probabilidades de transición entre ellos. Heisenberg introdujo el famoso "principio de incertidumbre", que establece que es imposible conocer simultáneamente y con precisión tanto la posición como la cantidad de movimiento de un electrón (\( \Delta x \, \Delta p \ge \hbar / 2 \)).
Este modelo transformó radicalmente la comprensión del átomo: los electrones ya no se veían como partículas descritas por órbitas clásicas, sino como entidades cuyo comportamiento solo podía expresarse en términos de magnitudes medibles. El modelo de Heisenberg es muy abstracto y no se presta a una ilustración clásica de electrones en órbita, a diferencia del de Bohr. Pero aún así puede representarse de manera simbólica y pedagógica.
A principios de la década de 1920 d.C., la física clásica ya no podía explicar la estabilidad de los átomos ni los espectros discretos observados experimentalmente. Erwin Schrödinger (1887-1961) desarrolló entonces un enfoque matemático basado en la mecánica ondulatoria. Reemplazó las trayectorias electrónicas fijas por una función de onda, cuyo módulo al cuadrado indica la probabilidad de presencia del electrón en el espacio.
Este enfoque describe los electrones como "nubes de probabilidad" organizadas en orbitales atómicos, caracterizados por números cuánticos que definen energía, forma y orientación. El modelo de Schrödinger explica la estabilidad de los átomos, los espectros atómicos y sirve como fundamento para toda la química cuántica moderna.
N.B.:
A diferencia de los modelos clásicos, el electrón no tiene una trayectoria definida. La mecánica cuántica solo describe probabilidades de presencia y energía.
| Modelo | Científico | Período | Característica principal |
|---|---|---|---|
| Átomo indivisible | Demócrito (c. 460-370 a.C.) | Siglo V a.C. | Partícula sin estructura interna |
| Átomo químico | John Dalton (1766-1844) | Siglo XIX d.C. | Masa definida, base de las reacciones químicas |
| Modelo de Thomson | Joseph John Thomson (1856-1940) | Finales del siglo XIX d.C. | Electrones incrustados en una carga positiva difusa |
| Modelo nuclear | Ernest Rutherford (1871-1937) | Principios del siglo XX d.C. | Núcleo central y electrones periféricos |
| Modelo cuantificado | Niels Bohr (1885-1962) | Principios del siglo XX d.C. | Niveles de energía discretos |
| Modelo ondulatorio | Louis de Broglie (1892-1987) | Siglo XX d.C. | Dualidad onda-partícula aplicada al electrón |
| Modelo matricial | Werner Heisenberg (1901-1976) | Siglo XX d.C. | Magnitudes observables, principio de incertidumbre, trayectorias indeterminadas |
| Modelo cuántico | Erwin Schrödinger (1887-1961) | Siglo XX d.C. | Función de onda y orbitales de probabilidad |