Das Atom in all seinen Formen: Von der antiken Intuition zur Quantenmechanik

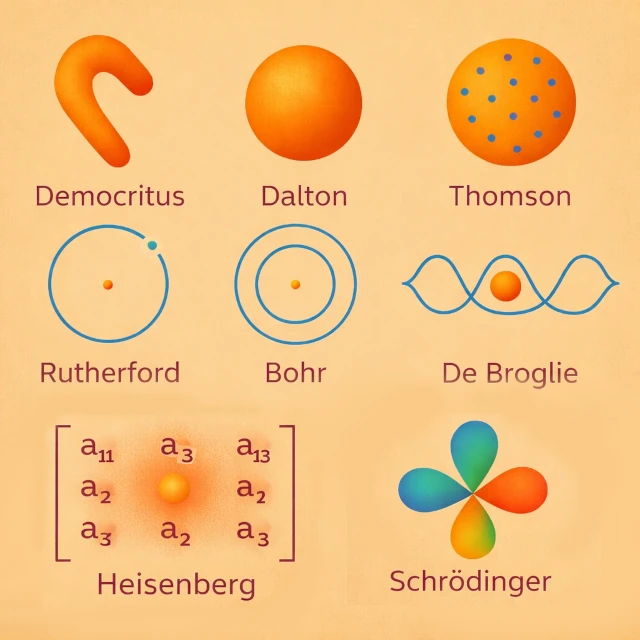
Historische Entwicklung der Atommodelle — Schematische Darstellung der Entwicklung der Atommodelle, vom unteilbaren Atom bis zu den Quantensorbitalen.
Bildquelle: astronoo.com (neues Fenster).

Wissenschaftliche Zusammenfassung

Der Artikel zeichnet die Entwicklung der Atommodellierung von den philosophischen Intuitionen des Demokrit (unteilbares Atom) bis zur probabilistischen Quantenmechanik nach. Diese wissenschaftliche Revolution durchläuft die Schlüsselmodelle: Dalton (kugelförmiges chemisches Atom), Thomson (in einer positiven Kugel verteilte Elektronen), Rutherford (kompakter Zentralkern), Bohr (quantisierte Bahnen), de Broglie (Welle-Teilchen-Dualismus), Heisenberg (Unschärferelation, unbestimmte Bahnen) und Schrödinger (Wahrscheinlichkeitswolken, Wellenfunktion). Jedes Modell korrigiert die Grenzen seines Vorgängers und spiegelt den Wandel von der klassischen zur Quantenphysik wider, in der das Elektron keine definierte Bahn mehr hat, sondern eine durch Atomorbitale beschriebene Aufenthaltswahrscheinlichkeit.

Wie hat sich die Modellierung des Atoms im Laufe der Wissenschaftsgeschichte entwickelt?

Die Darstellung des Atoms hat eine wissenschaftliche Revolution durchgemacht, von einem philosophischen Konzept hin zu einem probabilistischen Quantenmodell. Die Entwicklung beginnt mit Demokrit (unteilbares Atom), dann Dalton (kugelförmiges chemisches Atom), Thomson ("Rosinenkuchen"-Modell mit dispersen Elektronen), Rutherford (kompakter Zentralkern), Bohr (quantisierte Bahnen), de Broglie (Welle-Teilchen-Dualismus, stehende Wellen), Heisenberg (Matrizenmechanik, Unschärferelation) und Schrödinger (Wahrscheinlichkeitswolken, Wellenfunktion). Diese Abfolge von Modellen spiegelt den Wandel der Physik von der klassischen Mechanik zur Quantenmechanik wider, in der das Elektron keine definierte Bahn mehr hat, sondern eine Aufenthaltswahrscheinlichkeit.

Auch interessant

Setzen Sie Ihre Erkundung des Universums mit diesen Themen fort:

Philosophische Ursprünge des Atoms

Das Konzept des Atoms erschien im 5. Jahrhundert v. Chr. mit Demokrit (ca. 460-370 v. Chr.), der durch einen im Wesentlichen intuitiven und rationalen Ansatz die Existenz unteilbarer Teilchen postulierte, die sich im leeren Raum bewegen. Dieser Vorschlag basierte nicht auf experimenteller Beobachtung, sondern auf einer philosophischen Intuition, die das Problem der unendlichen Teilbarkeit der Materie lösen sollte. Kein Experiment konnte diese Hypothese damals testen. Das Atom wurde somit als die letzte Einheit der Materie gedacht, ohne innere Struktur oder messbare Eigenschaften. Für Demokrit besaß das Atom eine eigene Form, die intuitiv die Eigenschaften der Körper erklärte: Zum Beispiel verhakten sich hakenförmige Atome und ergaben raue Texturen, während runde oder glatte Atome flüssige oder weiche Substanzen bildeten.

Das Mittelalter: Zwischen aristotelischer Kontinuität und theologischem Atomismus

Im Mittelalter gab es keine physikalische Modellierung des Atoms im wissenschaftlichen Sinne, da das europäische Naturdenken weitgehend vom Erbe Aristoteles' geprägt war, für den die Materie kontinuierlich, unendlich teilbar und durch die vier Elemente (Erde, Wasser, Luft und Feuer) strukturiert war. Diese Sichtweise schloss die Existenz unteilbarer materieller Einheiten aus und widersprach explizit dem antiken Atomismus. Allerdings entwickelten im mittelalterlichen islamischen Raum einige Strömungen der rationalen Theologie, insbesondere der Kalām, eine Form des philosophischen Atomismus, in der die Welt aus diskreten Atomen bestand, die in jedem Augenblick durch den göttlichen Willen neu geschaffen wurden. Dieser mittelalterliche Atomismus beruhte weder auf Erfahrung noch auf mathematischen Gesetzen, sondern auf einer metaphysischen Intuition, die Kausalität, Kontingenz und göttliche Allmacht in Einklang bringen sollte. So blieb das Atom im Mittelalter ein spekulatives oder theologisches Konzept, ohne zu einem Gegenstand physikalischer Beschreibung oder Messung zu werden.

Die Geburt des wissenschaftlichen Atoms

Zu Beginn des 19. Jahrhunderts n. Chr. führte John Dalton (1766-1844) eine Atomtheorie ein, die auf der quantitativen Chemie basierte. Atome wurden zu chemischen und messbaren Entitäten, die durch ihre Masse gekennzeichnet sind, und waren für die Erhaltungssätze verantwortlich. Jedes chemische Element besteht aus identischen Atomen, die sich von denen anderer Elemente unterscheiden. Zum Beispiel erklärte Dalton bei der Bildung von Wasser, dass jedes Molekül aus der Kombination von zwei Wasserstoffatomen und einem Sauerstoffatom (H₂O) entsteht, entsprechend einfachen und konstanten Proportionen. Diese experimentelle Beobachtung zeigt, wie Atome chemische Reaktionen und ihre Proportionen steuern. Visuell kann man sich vorstellen, dass Dalton das Atom als eine kompakte und homogene Kugel ohne innere Struktur dachte, einfach als "ein kleines Materiekügelchen".

Das Thomson-Modell: Das "Rosinenkuchen"-Atom

Das Ende des 19. Jahrhunderts n. Chr. markierte einen entscheidenden Bruch in der Vorstellung des Atoms. 1897 entdeckte Joseph John Thomson (1856-1940) das Elektron und zeigte damit, dass das Atom nicht unteilbar ist. Er schlug ein Modell vor, in dem die Elektronen, die negative Ladung tragen, in einer diffusen Kugel positiver Ladung verteilt sind, wie Rosinen in einem Kuchen. Dieses Modell konnte bestimmte elektrische Eigenschaften der Atome erklären, aber nicht die Stabilität des Kerns, die später beobachtet wurde.

Das Rutherford-Modell: Das Kernatom

1911 interpretierte Ernest Rutherford (1871-1937) das Alpha-Teilchen-Streuexperiment. Er zeigte, dass die positive Ladung und der Großteil der Masse des Atoms in einem kompakten zentralen Kern konzentriert sind. Die Elektronen umkreisen diesen Kern, und das Atom wird zu einem System, das hauptsächlich aus leerem Raum besteht. Dieses Modell korrigierte die Grenzen des Thomson-Modells und legte den Grundstein für die späteren quantenmechanischen Entwicklungen.

Das Bohr-Modell: Quantisierung des Atoms

Das klassische Planetensystemmodell ist nach dem Elektromagnetismus instabil, da in der klassischen Physik eine beschleunigte Ladung wie ein Elektron in der Umlaufbahn elektromagnetische Energie abstrahlt, allmählich seine kinetische Energie verliert und unweigerlich in den Kern spiralt. Um diesen Widerspruch zu lösen, führte Niels Bohr (1885-1962) 1913 quantisierte Elektronenbahnen ein. Elektronen können nur bestimmte Energieniveaus besetzen, was die diskreten Atomspektren erklärt.

Das Wellenmodell von Louis de Broglie: Stehende Welle

Zu Beginn des 20. Jahrhunderts n. Chr. schlug Louis de Broglie (1892-1987) eine konzeptionelle Revolution vor: Das Elektron und allgemein jedes materielle Teilchen besitzt sowohl eine "Teilchen"- als auch eine "Wellen"-Natur. Diese Idee, Welle-Teilchen-Dualismus genannt, legt nahe, dass das Elektron, das den Kern umkreist, als "stehende Welle" beschrieben werden kann, deren Wellenlänge umgekehrt proportional zu seinem Impuls ist: \( \lambda = h / p \), wobei \( \lambda \) die Wellenlänge, \( h \) das Plancksche Wirkungsquantum und \( p \) der Impuls ist.

Das de-Broglie-Modell erklärt, warum nur bestimmte Bahnen im Bohrschen Atom stabil sind: Das Elektron kann nur die Bahnen besetzen, für die seine Wellenlänge einen vollständigen Zyklus um den Kern bildet und eine Resonanzbedingung schafft. Dieses Konzept war ein wesentlicher Schritt zur "Quantenmechanik", da es die korpuskularen Eigenschaften der Teilchen mit ihrem Wellenverhalten verband und den Weg für die Schrödinger-Gleichung ebnete.

Das Heisenberg-Modell: Matrizenmechanik

In den 1920er Jahren n. Chr. schlug Werner Heisenberg (1901-1976) einen neuen Ansatz für das Atom vor, der auf den Prinzipien der Quantenmechanik basierte. Sein Modell, die "Matrizenmechanik", versuchte nicht, die Bahn der Elektronen um den Kern zu beschreiben, sondern nur die "beobachtbaren Größen" wie die Energien der atomaren Niveaus und die Übergangswahrscheinlichkeiten zwischen ihnen. Heisenberg führte das berühmte "Unschärfeprinzip" ein, das besagt, dass es unmöglich ist, gleichzeitig und genau sowohl den Ort als auch den Impuls eines Elektrons zu kennen (\( \Delta x \, \Delta p \ge \hbar / 2 \)).

Dieses Modell veränderte das Verständnis des Atoms radikal: Elektronen wurden nicht mehr als Teilchen gesehen, die durch klassische Bahnen beschrieben werden, sondern als Entitäten, deren Verhalten nur durch messbare Größen ausgedrückt werden kann. Heisenbergs Modell ist sehr abstrakt und eignet sich nicht für eine klassische Illustration von Elektronen in Umlaufbahnen, im Gegensatz zu Bohrs Modell. Aber es kann trotzdem symbolisch und pädagogisch dargestellt werden.

Das quantenmechanische Modell von Schrödinger: Wahrscheinlichkeitswolken

Zu Beginn der 1920er Jahre n. Chr. konnte die klassische Physik die Stabilität der Atome und die experimentell beobachteten diskreten Spektren nicht mehr erklären. Erwin Schrödinger (1887-1961) entwickelte daraufhin einen mathematischen Ansatz, der auf der Wellenmechanik basierte. Er ersetzte die festen Elektronenbahnen durch eine Wellfunktion (mathematische Funktion, Lösung der Schrödinger-Gleichung, die die Aufenthaltswahrscheinlichkeit des Elektrons darstellt), deren Betragsquadrat die Aufenthaltswahrscheinlichkeit des Elektrons im Raum angibt.

Dieser Ansatz beschreibt Elektronen als "Wahrscheinlichkeitswolken", die in Atomorbitalen (raumbereiche, in denen die Aufenthaltswahrscheinlichkeit des Elektrons signifikant ist) organisiert sind, die durch Quantenzahlen gekennzeichnet sind, die Energie, Form und Orientierung definieren. Das Schrödinger-Modell erklärt die Stabilität der Atome, die Atomspektren und dient als Grundlage für die gesamte moderne Quantenchemie.

N.B.:
Im Gegensatz zu klassischen Modellen hat das Elektron keine definierte Bahn. Die Quantenmechanik beschreibt nur Aufenthalts- und Energie-Wahrscheinlichkeiten.

Vergleich der wichtigsten Atommodelle

Entwicklung der physikalischen Atommodelle
Modell	Wissenschaftler	Zeitraum	Hauptmerkmal
Unteilbares Atom	Demokrit (ca. 460-370 v. Chr.)	5. Jahrhundert v. Chr.	Teilchen ohne innere Struktur
Chemisches Atom	John Dalton (1766-1844)	19. Jahrhundert n. Chr.	Definierte Masse, Grundlage chemischer Reaktionen
Thomson-Modell	Joseph John Thomson (1856-1940)	Ende 19. Jahrhundert n. Chr.	Elektronen in einer diffusen positiven Ladung
Kernmodell	Ernest Rutherford (1871-1937)	Anfang 20. Jahrhundert n. Chr.	Zentraler Kern und periphere Elektronen
Quantisiertes Modell	Niels Bohr (1885-1962)	Anfang 20. Jahrhundert n. Chr.	Diskrete Energieniveaus
Wellenmodell	Louis de Broglie (1892-1987)	20. Jahrhundert n. Chr.	Welle-Teilchen-Dualismus auf das Elektron angewandt
Matrizenmodell	Werner Heisenberg (1901-1976)	20. Jahrhundert n. Chr.	Beobachtbare Größen, Unschärfeprinzip, unbestimmte Bahnen
Quantenmodell	Erwin Schrödinger (1887-1961)	20. Jahrhundert n. Chr.	Wellenfunktion und Wahrscheinlichkeitsorbitale

FAQ: Alles über die Modellierung des Atoms

Warum ersetzte Rutherfords Modell Thomsons Modell?

Thomsons "Rosinenkuchen"-Modell schlug vor, dass negative Elektronen in einer Kugel diffuser positiver Ladung verteilt seien. 1911 führte Rutherford ein Experiment zur Streuung von Alphateilchen an einer dünnen Goldfolie durch. Er beobachtete, dass einige Teilchen zurückgestreut wurden, was die Existenz eines kompakten, massiven Zentralkerns bewies, der den größten Teil der Masse und die gesamte positive Ladung des Atoms konzentriert. Thomsons Modell konnte diese Ergebnisse nicht erklären, Rutherfords Kernmodell hingegen schon.

Was ist der grundlegende Unterschied zwischen dem Bohr-Modell und dem Schrödinger-Modell?

Bohrs Modell (1913) schlug quantisierte kreisförmige Elektronenbahnen vor, wie Planeten um die Sonne, jedoch mit diskreten Energieniveaus. Schrödingers Modell (1920er Jahre) ersetzte diese festen Bahnen durch eine Wellenfunktion, deren Quadrat die Aufenthaltswahrscheinlichkeit des Elektrons angibt. Das Elektron hat keine definierte Bahn mehr, sondern bildet „Wahrscheinlichkeitswolken“, die als Atomorbitale bezeichnet werden. Schrödingers Modell ist genauer und dient als Grundlage der modernen Quantenchemie.

Was ist der Welle-Teilchen-Dualismus und welchen Beitrag leistet er zur Atommodellierung?

Der von Louis de Broglie zu Beginn des 20. Jahrhunderts vorgeschlagene Welle-Teilchen-Dualismus besagt, dass jedes materielle Teilchen (wie das Elektron) sowohl Teilchen- als auch Wellennatur besitzt, mit einer zugehörigen Wellenlänge λ = h/p (wobei h das Plancksche Wirkungsquantum und p der Impuls ist). Auf das Atom angewendet, erklärt diese Idee, warum nur bestimmte Bahnen im Bohr-Modell stabil sind: Das Elektron kann nur die Bahnen besetzen, auf denen seine Wellenlänge einen vollständigen Umlauf um den Kern bildet (Resonanzbedingung). Dieses Konzept ebnete den Weg für die Schrödinger-Gleichung und die Quantenmechanik.