De la Neurona Biológica a la Neurona Formal: Simplificación del Cerebro

Origen del concepto de neurona formal

McCulloch, un neurofisiólogo, y Pitts, un lógico, conceptualizaron las neuronas formales como unidades de cálculo para construir redes neuronales artificiales en su artículo de 1943 titulado "A Logical Calculus of the Ideas Immanent in Nervous Activity".
En esta publicación, presentaron un modelo matemático simple pero potente de neuronas y redes neuronales. Su objetivo era comprender cómo el cerebro podría realizar operaciones lógicas, como las que realiza una computadora.

Una abstracción matemática de la neurona biológica

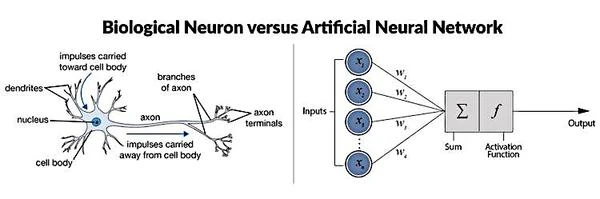
Una neurona formal es una representación matemática e informática de una neurona biológica. Tiene varias entradas y una salida que corresponde a las dendritas y al cono de emergencia de la neurona biológica, punto de partida del axón. Las acciones excitadoras e inhibitorias de las sinapsis están representadas por coeficientes numéricos (pesos sinápticos) asociados a las entradas.

El papel de las entradas ponderadas

En su modelo, una neurona formal toma entradas binarias (activadas o desactivadas) de otras neuronas o fuentes externas. Cada entrada está ponderada por un peso específico, que puede representar la fuerza de la conexión sináptica entre las neuronas en el modelo biológico.

La función de activación y el umbral

En función de la suma ponderada de sus entradas, la neurona formal produce una salida binaria, que puede estar activada (1) o desactivada (0). Esta salida generalmente se determina aplicando una función de activación \( f \), que convierte la suma ponderada \( S \) en una salida \( y \) según un umbral \( \theta \):

\( y = f(S - \theta) \)

En el modelo inicial de McCulloch y Pitts, la función \( f \) es una función de Heaviside:

\( f(S - \theta) = \begin{cases} 1 & \text{si } S \geq \theta \\ 0 & \text{si } S < \theta \end{cases} \)

De las operaciones lógicas a los fundamentos de la inteligencia artificial

McCulloch y Pitts utilizaron estas neuronas formales para construir redes neuronales artificiales capaces de realizar operaciones lógicas como la conjunción (AND), la disyunción (OR) y la negación (NOT). Demostraron que incluso con estas reglas de conexión simples, era posible construir redes neuronales capaces de realizar operaciones lógicas complejas. Esta formalización de las neuronas fue crucial para permitir un análisis matemático y una modelización de las redes neuronales, sentando así las bases para futuras investigaciones en inteligencia artificial y neurociencia computacional (aplicación de la informática a la comprensión del sistema nervioso).

N.B.:
Las neuronas formales de McCulloch y Pitts no tienen en cuenta el tiempo, las señales continuas ni la plasticidad sináptica. Sin embargo, constituyen la primera formalización matemática del concepto de red neuronal, en el origen de la inteligencia artificial moderna.