From Biological Neuron to Formal Neuron: Simplifying the Brain

Origin of the Formal Neuron Concept

McCulloch, a neurophysiologist, and Pitts, a logician, conceptualized formal neurons as computational units to build artificial neural networks in their 1943 paper titled "A Logical Calculus of the Ideas Immanent in Nervous Activity".
In this publication, they presented a simple yet powerful mathematical model of neurons and neural networks. Their goal was to understand how the brain could perform logical operations, such as those carried out by a computer.

A Mathematical Abstraction of the Biological Neuron

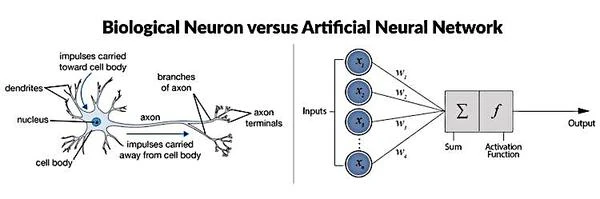
A formal neuron is a mathematical and computational representation of a biological neuron. It has multiple inputs and one output, corresponding to the dendrites and the axon hillock of the biological neuron, the starting point of the axon. The excitatory and inhibitory actions of synapses are represented by numerical coefficients (synaptic weights) associated with the inputs.

The Role of Weighted Inputs

In their model, a formal neuron takes binary inputs (activated or deactivated) from other neurons or external sources. Each input is weighted by a specific weight, which can represent the strength of the synaptic connection between neurons in the biological model.

The Activation Function and Threshold

Based on the weighted sum of its inputs, the formal neuron produces a binary output, which can be activated (1) or deactivated (0). This output is generally determined by applying an activation function \( f \), which converts the weighted sum \( S \) into an output \( y \) according to a threshold \( \theta \):

\( y = f(S - \theta) \)

In the initial model by McCulloch and Pitts, the function \( f \) is a Heaviside function:

\( f(S - \theta) = \begin{cases} 1 & \text{if } S \geq \theta \\ 0 & \text{if } S <\theta \end{cases} \)

From Logical Operations to the Foundations of Artificial Intelligence

McCulloch and Pitts used these formal neurons to build artificial neural networks capable of performing logical operations such as conjunction (AND), disjunction (OR), and negation (NOT). They demonstrated that even with these simple connection rules, it was possible to build neural networks capable of performing complex logical operations. This formalization of neurons was crucial for enabling mathematical analysis and modeling of neural networks, thus laying the foundation for future research in artificial intelligence and computational neuroscience (the application of computer science to understanding the nervous system).

N.B.:
McCulloch and Pitts' formal neurons do not account for time, continuous signals, or synaptic plasticity. However, they represent the first mathematical formalization of the concept of a neural network, at the origin of modern artificial intelligence.