Dernière mise à jour : 29 juin 2024

Du Neurone Biologique au Neurone Formel : Simplification du Cerveau

Étude des principes computationnels du cerveau

Origine du concept de neurone formel

McCulloch, un neurophysiologiste, et Pitts, un logicien, ont conceptualisé les neurones formels comme des unités de calcul pour construire des réseaux neuronaux artificiels dans leur article de 1943 intitulé "A Logical Calculus of the Ideas Immanent in Nervous Activity".
Dans cette publication, ils ont présenté un modèle mathématique simple mais puissant des neurones et des réseaux neuronaux. Leur objectif était de comprendre comment le cerveau pourrait effectuer des opérations logiques, telles que celles effectuées par un ordinateur.

Une abstraction mathématique du neurone biologique

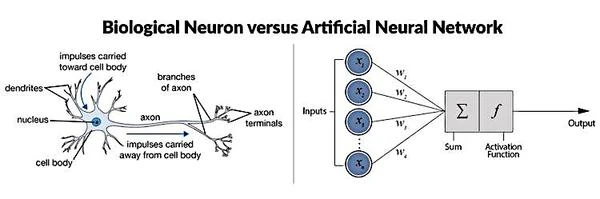
Un neurone formel est une représentation mathématique et informatique d'un neurone biologique. Il possède plusieurs entrées et une sortie qui correspond aux dendrites et au cône d'émergence du neurone biologique, point de départ de l'axone. Les actions excitatrices et inhibitrices des synapses sont représentées par des coefficients numériques (poids synaptiques) associés aux entrées.

Le rôle des entrées pondérées

Dans le cadre de leur modèle, un neurone formel prend des entrées binaires (activées ou désactivées) provenant d'autres neurones ou de sources externes. Chaque entrée est pondérée par un poids spécifique, qui peut représenter la force de la connexion synaptique entre les neurones dans le modèle biologique.

La fonction d’activation et le seuil

En fonction de la somme pondérée de ses entrées, le neurone formel produit une sortie binaire, qui peut être activée (1) ou désactivée (0). Cette sortie est généralement déterminée par l'application d'une fonction d'activation \( f \), qui convertit la somme pondérée \( S \) en une sortie \( y \) selon un seuil \( \theta \) :

\( y = f(S - \theta) \)

Dans le modèle initial de McCulloch et Pitts, la fonction \( f \) est une fonction de Heaviside :

\( f(S - \theta) = \begin{cases} 1 & \text{si } S \geq \theta \\ 0 & \text{si } S < \theta \end{cases} \)

Des opérations logiques aux bases de l’intelligence artificielle

McCulloch et Pitts ont utilisé ces neurones formels pour construire des réseaux neuronaux artificiels capables de réaliser des opérations logiques telles que la conjonction (AND), la disjonction (OR) et la négation (NOT). Ils ont démontré que même avec ces règles de connexion simples, il était possible de construire des réseaux neuronaux capables de réaliser des opérations logiques complexes. Cette formalisation des neurones a été cruciale pour permettre une analyse mathématique et une modélisation des réseaux neuronaux, jetant ainsi les bases de la recherche future en intelligence artificielle et en neurosciences computationnelles (application de l'informatique à la compréhension du système nerveux).

N.B. :
Les neurones formels de McCulloch et Pitts ne tiennent pas compte du temps, des signaux continus ni de la plasticité synaptique. Ils constituent cependant la première formalisation mathématique du concept de réseau neuronal, à l’origine de l’intelligence artificielle moderne.