Do Neurônio Biológico ao Neurônio Formal: Simplificação do Cérebro

Origem do conceito de neurônio formal

McCulloch, um neurofisiologista, e Pitts, um lógico, conceituaram os neurônios formais como unidades de cálculo para construir redes neurais artificiais em seu artigo de 1943 intitulado "A Logical Calculus of the Ideas Immanent in Nervous Activity".
Nesta publicação, eles apresentaram um modelo matemático simples, porém poderoso, de neurônios e redes neurais. Seu objetivo era entender como o cérebro poderia realizar operações lógicas, como as executadas por um computador.

Uma abstração matemática do neurônio biológico

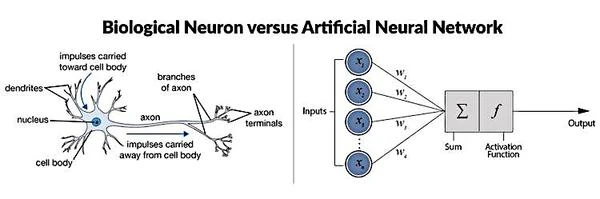
Um neurônio formal é uma representação matemática e computacional de um neurônio biológico. Ele possui várias entradas e uma saída que corresponde às dendrites e ao cone de emergência do neurônio biológico, ponto de partida do axônio. As ações excitatórias e inibitórias das sinapses são representadas por coeficientes numéricos (pesos sinápticos) associados às entradas.

O papel das entradas ponderadas

Em seu modelo, um neurônio formal recebe entradas binárias (ativadas ou desativadas) de outros neurônios ou fontes externas. Cada entrada é ponderada por um peso específico, que pode representar a força da conexão sináptica entre os neurônios no modelo biológico.

A função de ativação e o limiar

Com base na soma ponderada de suas entradas, o neurônio formal produz uma saída binária, que pode ser ativada (1) ou desativada (0). Esta saída é geralmente determinada pela aplicação de uma função de ativação \( f \), que converte a soma ponderada \( S \) em uma saída \( y \) de acordo com um limiar \( \theta \):

\( y = f(S - \theta) \)

No modelo inicial de McCulloch e Pitts, a função \( f \) é uma função de Heaviside:

\( f(S - \theta) = \begin{cases} 1 & \text{se } S \geq \theta \\ 0 & \text{se } S < \theta \end{cases} \)

Das operações lógicas às bases da inteligência artificial

McCulloch e Pitts usaram esses neurônios formais para construir redes neurais artificiais capazes de realizar operações lógicas como conjunção (AND), disjunção (OR) e negação (NOT). Eles demonstraram que, mesmo com essas regras de conexão simples, era possível construir redes neurais capazes de realizar operações lógicas complexas. Esta formalização dos neurônios foi crucial para permitir uma análise matemática e modelagem de redes neurais, lançando assim as bases para pesquisas futuras em inteligência artificial e neurociência computacional (aplicação da ciência da computação à compreensão do sistema nervoso).

N.B.:
Os neurônios formais de McCulloch e Pitts não levam em consideração o tempo, sinais contínuos ou plasticidade sináptica. No entanto, eles representam a primeira formalização matemática do conceito de rede neural, na origem da inteligência artificial moderna.