Letzte Aktualisierung: 29. Juni 2024

Vom biologischen Neuron zum formalen Neuron: Vereinfachung des Gehirns

Untersuchung der Rechenprinzipien des Gehirns

Ursprung des Konzepts des formalen Neurons

McCulloch, ein Neurophysiologe, und Pitts, ein Logiker, konzipierten in ihrer Arbeit von 1943 mit dem Titel „A Logical Calculus of the Ideas Immanent in Nervous Activity“ formale Neuronen als Recheneinheiten für den Aufbau künstlicher neuronaler Netze.
In dieser Veröffentlichung präsentierten sie ein einfaches, aber leistungsstarkes mathematisches Modell von Neuronen und neuronalen Netzen. Ihr Ziel war es zu verstehen, wie das Gehirn logische Operationen ausführen kann, wie sie beispielsweise ein Computer ausführt.

Eine mathematische Abstraktion des biologischen Neurons

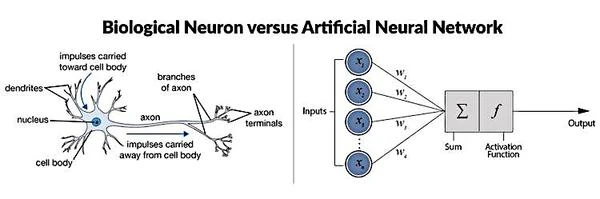
Ein formales Neuron ist eine mathematische und rechnerische Darstellung eines biologischen Neurons. Es verfügt über mehrere Eingänge und einen Ausgang, der den Dendriten und dem Austrittskegel des biologischen Neurons, dem Ausgangspunkt des Axons, entspricht. Die erregenden und hemmenden Wirkungen von Synapsen werden durch numerische Koeffizienten (synaptische Gewichte) dargestellt, die den Eingaben zugeordnet sind.

Die Rolle gewichteter Eingaben

Nach ihrem Modell nimmt ein formales Neuron binäre Eingaben (ein oder aus) von anderen Neuronen oder externen Quellen entgegen. Jede Eingabe wird mit einem bestimmten Gewicht gewichtet, das die Stärke der synaptischen Verbindung zwischen Neuronen im biologischen Modell darstellen kann.

Die Aktivierungsfunktion und der Schwellenwert

Abhängig von der gewichteten Summe seiner Eingaben erzeugt das formale Neuron eine binäre Ausgabe, die aktiviert (1) oder deaktiviert (0) werden kann. Diese Ausgabe wird im Allgemeinen durch Anwenden einer Aktivierungsfunktion \( f \) bestimmt, die die gewichtete Summe \( S \) in eine Ausgabe \( y \) gemäß einem Schwellenwert \( \theta \) umwandelt:

\( y = f(S - \theta) \)

Im ursprünglichen Modell von McCulloch und Pitts ist die Funktion \( f \) eine Heaviside-Funktion:

\( f(S - \theta) = \begin{cases} 1 & \text{si } S \geq \theta \\ 0 & \text{si } S < \theta \end{Fälle} \)

Von logischen Operationen bis zu den Grundlagen der künstlichen Intelligenz

McCulloch und Pitts nutzten diese formalen Neuronen, um künstliche neuronale Netze zu konstruieren, die in der Lage sind, logische Operationen wie Konjunktion (AND), Disjunktion (OR) und Negation (NOT) durchzuführen. Sie zeigten, dass es selbst mit diesen einfachen Verbindungsregeln möglich war, neuronale Netze aufzubauen, die komplexe logische Operationen ausführen können. Diese Formalisierung von Neuronen war entscheidend für die mathematische Analyse und Modellierung neuronaler Netze und legte damit den Grundstein für zukünftige Forschungen in den Bereichen künstliche Intelligenz und Computational Neuroscience (Anwendung der Informatik zum Verständnis des Nervensystems).

Hinweis: :
Formale McCulloch- und Pitts-Neuronen berücksichtigen weder Zeit noch kontinuierliche Signale noch synaptische Plastizität. Sie stellen jedoch die erste mathematische Formalisierung des Konzepts des neuronalen Netzwerks dar, das den Ursprung der modernen künstlichen Intelligenz bildet.