Die große Gabelung, die unsere Welt aufrütteln wird: Überleben oder Zusammenbruch?

Turbulenzzonen für den Planeten

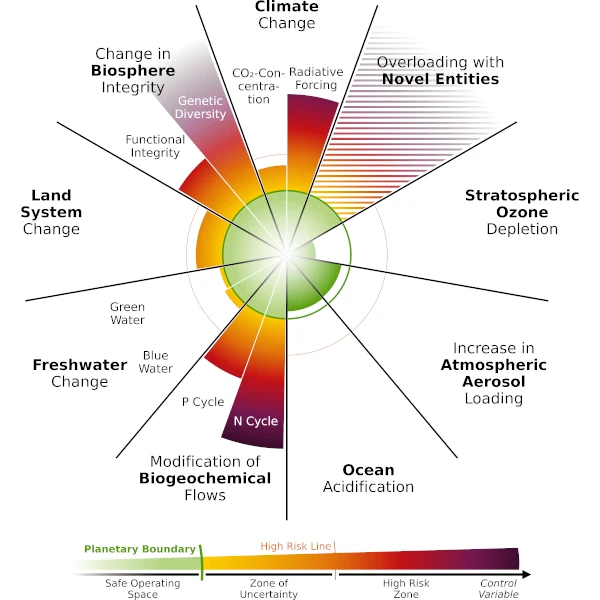
Das Erdsystem ist aufgrund seiner vielfältigen miteinander verbundenen Komponenten, seiner nichtlinearen Rückkopplungen und seines entstehenden Verhaltens komplex, das allein anhand der Eigenschaften seiner einzelnen Elemente schwer vorherzusagen ist.

Die großen interagierenden Subsysteme – Klima, Ozeane, Süßwasser, Biosphäre und menschliche Aktivitäten – folgen keiner einfachen Ursache-Wirkungs-Beziehung, sondern können sich auf unvorhersehbare Weise verstärken. Es muss nur eine einzige Schwelle erreicht werden, damit das System umkippt und kaskadierende Brüche erzeugt. Bei diesen irreversiblen Schwellenwerten handelt es sich um „Points of no Return“ und nicht um „Passing Points“ bei allmählichen Veränderungen.

Die Bifurkation ist in der Physik ein grundlegendes Konzept

In der Physik und Mathematik bezeichnet eine Bifurkation eine qualitative Änderung im Verhalten eines dynamischen Systems, wenn einer seiner Parameter einen kritischen Wert überschreitet. Dieses für die Theorie komplexer Systeme zentrale Konzept erklärt, wie kleine Modifikationen plötzliche und radikale Veränderungen bewirken können.

Während einer Bifurkation (gegabelte Gabelung), teilt sich ein stabiler Gleichgewichtspunkt in zwei neue stabile Lösungen, während er selbst instabil wird, ist der Übergang jenseits der Schwelle irreversibel. Zum Beispiel :

• Magnetisierungsübergang(Ising-Modell, Ferromagnetismus), unterhalb einer kritischen Temperatur treten zwei stabile Magnetisierungen auf, darüber keine Nettomagnetisierung.

Während einer Bifurkation (Sattelknotengabelung oder Faltengabelung), treffen zwei Fixpunkte, einer stabil und einer instabil, aufeinander und verschwinden bei einem strukturellen Zusammenbruch. Zum Beispiel :

• Ökologische Katastrophe(Seewasserqualität), unterhalb eines Phosphorgehalts ist das Seewasser klar (stabiles System). Ein leichter Anstieg des Phosphors hebt das klare Gleichgewicht auf: Das System verschiebt sich irreversibel in Richtung des trüben Sees.

Während einer Bifurkation (Hopf-Gabelung) wird ein stabiler Fixpunkt instabil, wenn sich die Parameter des Systems (langsam oder über einen Schwellenwert) entwickeln und gleichzeitig ein stabiler Grenzzyklus entsteht. Zum Beispiel :

• Herzzelle(Aktionspotential in der Zelle. Unterhalb einer Erregbarkeitsschwelle bleibt die Zelle im Ruhezustand stabil. Darüber hinaus wird Ruhe instabil und das System erzeugt periodische autonome Impulse. Das Herz beginnt spontan zu schlagen: Auftreten eines stabilen Grenzzyklus.

Welchen stabilen Zustand droht unsere Gesellschaft zu verlieren?

Unsere Welt interagiert mit mehreren Systemen – klimatisch (Wolken und Wolkendecke usw.), ökologisch (Agrarkrise und sinkende Erträge usw.), sozial und politisch (demokratische Regime usw.), wirtschaftlich und technologisch (Finanzmärkte usw.), kulturell und kognitiv (Zusammenbruch gemeinsamer Narrative usw.).

Diese Gleichgewichte scheinen nachhaltig zu sein, werden aber in Wirklichkeit in dynamischen Regimen aufrechterhalten, die auf kritische Parameter reagieren. Wenn ein Parameter einen Schwellenwert überschreitet, kann es zu einer Bifurkation des Systems kommen, das heißt, dass es plötzlich seine ursprüngliche Stabilität verliert und sich in einen völlig anderen unvorhersehbaren Zustand entwickelt. Je nach Art der Bifurkation können die Übergänge mehr oder weniger abrupt sein.

Dieses in der Physik, Mathematik und Biologie bekannte Phänomen gilt auch für unsere Gesellschaften. Im System häufen sich schwache Anzeichen (geopolitische Spannungen, globale Erwärmung, Rückgang der Artenvielfalt, technologische Interdependenz, Anstieg der globalen Verschuldung, Konzentration des Kapitals, Wachstum populistischer Bewegungen, allgemeines Misstrauen gegenüber der Wissenschaft, wachsende Spannungen um Trinkwasser, beschleunigte Alterung der Bevölkerung, schnelle Urbanisierung, Explosion von Fake News, Veränderung der gemeinsamen Realität, Wachstum unkontrollierbarer KI, Anpassungsfähigkeit von Gesellschaften usw.)

Gabelung und Zukunft des Weltsystems: Verlust der Vorhersehbarkeit

Wenn das „Weltsystem„nähert sich einem kritischen Punkt, die Gabelung steht unmittelbar bevor und das System steht kurz vor einem radikalen Wandel.“ Wir alle haben das Gefühl, dass sich unser Planet näherteinen oder mehrere kritische Schwellenwertewo es zu großen Gabelungen mit irreversiblen Folgen für die menschlichen Gesellschaften kommen könnte. Angesichts dieser vielfältigen potenziellen Wendepunkte steht die Menschheit vor einer beispiellosen Herausforderung: Das Verständnis dieser kritischen Schwellenwerte ermöglicht es uns, uns auf unvermeidliche Veränderungen vorzubereiten.

Paradoxerweise könnte der stabile Zustand, den unsere Gesellschaft zu verlieren droht, durchaus der seinStabilität der globalen Vorhersagbarkeit, also die Fähigkeit, die Zukunft mittelfristig zu projizieren. Dies könnte eine Reihe kaskadierender Folgen im Zusammenhang mit gekoppelten Instabilitäten (ökologische, energetische, soziale, technologische usw.) auslösen.

Konkrete Folgen des Verlustes dieses stabilen Zustandes

• Ende zuverlässiger Vorhersagemodelle: Unfähigkeit, über 10, 20 oder 50 Jahre zu planen.
• Vermehrung von „Finanzblasen“: Die Wirtschaft wird chaotisch oder unregelmäßig.
• Auftreten häufigerer Extremphänomene: Das lokale und globale Klima wird schwierig zu modellieren.
• Beschleunigte soziale Veränderungen: Normen, Berufe, Familien- oder Bildungsstrukturen ändern sich zu schnell, als dass sich Generationen daran anpassen könnten.
• Institutionelle Fragmentierung: Der demokratische Attraktor verliert an Stabilität und es entstehen neue, radikalere Attraktoren.
• Individuelle und kollektive Desorientierung: Instabilität kultureller, pädagogischer und beruflicher Maßstäbe.
• Anhäufung von Stress: Permanente Hyperadaptation oder systemische Ermüdung mit dem Risiko eines lokalen und dann globalen Versagens.
• Entstehung neuer Attraktoren:Es können unerwartete alternative Regime entstehen: technozentrische Gesellschaften, digitale Fragmentierung, Ökodiktaturen, Neotribalismus.