最終更新日：2024年6月29日

生物学的ニューロンから形式ニューロンへ：脳の単純化

形式ニューロンの概念の起源

神経生理学者のマカロックと論理学者のピッツは、1943年の論文「A Logical Calculus of the Ideas Immanent in Nervous Activity」で、人工神経ネットワークを構築するための計算単位として形式ニューロンを概念化しました。
この論文では、ニューロンと神経ネットワークの単純ながら強力な数学モデルを提示しました。彼らの目標は、脳がコンピュータが行うような論理演算をどのように実行できるかを理解することでした。

生物学的ニューロンの数学的抽象化

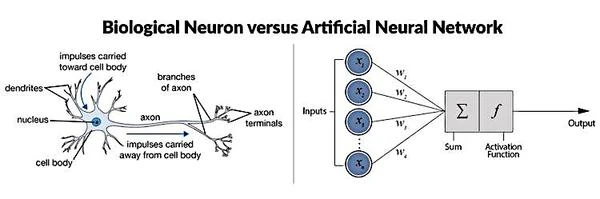
形式ニューロンは、生物学的ニューロンの数学的および計算機的表現です。複数の入力と1つの出力を持ち、生物学的ニューロンの樹状突起と軸索丘（軸索の出発点）に対応しています。シナプスの興奮作用と抑制作用は、入力に関連付けられた数値係数（シナプス重み）によって表現されます。

重み付き入力の役割

彼らのモデルでは、形式ニューロンは他のニューロンまたは外部ソースからの二進入力（活性化または非活性化）を受け取ります。各入力は特定の重みによって重み付けられ、生物学的モデルにおけるニューロン間のシナプス接続の強度を表すことができます。

活性化関数と閾値

重み付き入力の合計に基づいて、形式ニューロンは二進出力（活性化（1）または非活性化（0））を生成します。この出力は通常、重み付き合計 \( S \) を閾値 \( \theta \) に応じて出力 \( y \) に変換する活性化関数 \( f \) を適用することによって決定されます：

\( y = f(S - \theta) \)

マカロックとピッツの初期モデルでは、関数 \( f \) はヘヴィサイド関数です：

\( f(S - \theta) = \begin{cases} 1 & \text{もし } S \geq \theta \\ 0 & \text{もし } S < \theta \end{cases} \)

論理演算から人工知能の基礎へ

マカロックとピッツは、これらの形式ニューロンを使用して、論理積（AND）、論理和（OR）、否定（NOT）などの論理演算を実行できる人工神経ネットワークを構築しました。彼らは、これらの単純な接続規則でも、複雑な論理演算を実行できる神経ネットワークを構築できることを実証しました。ニューロンのこの形式化は、神経ネットワークの数学的分析とモデリングを可能にし、人工知能と計算神経科学（神経系の理解にコンピュータサイエンスを応用する分野）の将来の研究の基礎を築きました。

N.B.:
マカロックとピッツの形式ニューロンは、時間、連続信号、シナプス可塑性を考慮していません。しかし、これらは神経ネットワークの概念の最初の数学的形式化であり、現代の人工知能の起源となっています。