Atomorbitale verstehen

Bildbeschreibung: DERAtomorbitale des Wasserstoffatomswerden als Funktion der Energie des Elektrons und seines Drehimpulses dargestellt. Das Energieniveau steigt von oben nach unten (n = 1, 2, 3, 4, 5) und der Drehimpuls nimmt von links nach rechts zu (l = s, p, d, f, g). Farben: Schwarz: Wahrscheinlichkeitsdichte Null (das Elektron geht nie dorthin). Weiß: maximale Dichte (das Elektron passiert sie oft). Orangerot: mittlere Dichte. Quantenzahlen: n: Hauptquantenzahl, definiert das Energieniveau. l: Sekundär- oder Orbitalquantenzahl, definiert die Unterschalen (s, p, d, f, g...). m: magnetische Quantenzahl, repräsentiert die Orientierungen der Orbitale. s: Spinquantenzahl, quantifiziert den Eigendrehimpuls des Elektrons. Diese Darstellung zeigt die Wahrscheinlichkeitsdichte, das Elektron in verschiedenen Bereichen um den Kern herum zu finden. Bildquelle: GNU Free Documentation License.

Struktur des Atoms

Durch die Betrachtung der kleinsten Bestandteile der Materie werden Wissenschaftler (20. Jahrhundert) die Funktionsweise des gesamten Universums erklären.

Ein Atom besteht aus einem Kern, um den sich ein oder mehrere Elektronen bewegen. Was den Kern charakterisiert, ist seine Anzahl an Protonen (Z), die zwischen 1 und 110 liegt. Dies bestimmt das Element, zum Beispiel hat Eisen (Fe26) 26 Protonen, 26 ist seine Ordnungszahl (Z). Die Anzahl der Neutronen (N), die von 0 bis 160 reicht, charakterisiert die Isotope des Elements, zum Beispiel hat Wasserstoff (H1) ein Proton und keine Neutronen, Deuterium (H2) hat ein Proton und ein Neutron, Tritium (H3) hat ein Proton und zwei Neutronen.

Diese drei Formen von Wasserstoff haben nur ein Elektron, da es nur eine elektrische Ladung gibt, das einzelne Proton.

Bitte beachten Sie, dass wir nur im Fall von Wasserstoff den Isotopen des Elements einen anderen Namen geben. In allen anderen Fällen geben wir nur die Anzahl der Nukleonen an, wodurch wir die Anzahl der Neutronen ermitteln können. Zum Beispiel hat Eisen (Fe26) mehrere Isotope, einschließlich Fe56. Wir verstehen, dass Fe56 30 Neutronen hat, Fe57 hat 31 Neutronen, Fe58 hat 32 Neutronen, die Anzahl der Neutronen unterscheidet die Isotope deutlich.

Im Atom sind es die Elektronen, die der Materie ihre Konsistenz verleihen, dennoch ist es sehr leicht (≈10^-27G). Das Proton ist etwa 2000-mal schwerer und konzentriert den größten Teil der Atommasse (99,99 %). Für stabile Atome liegt die Masse zwischen 1,674×10^-24g für Wasserstoff und 3,953×10^-22g für Uran.

Seit 1811 kennen wir auch die ungefähre Größe eines Atoms,Amedeo Avogadro(1776-1856) schätzte die Größe von Atomen auf 10-10 Meter (Angström), also etwas mehr als 10 Millionstel Millimeter. Im Jahr 1911Ernest Rutherford(1871-1937) entdeckte den Atomkern.

Rutherford klärt die Struktur des Atoms auf, indem er ein Goldblech mit Partikeln bombardiert, die beim radioaktiven Zerfall von Uran entstehen. Daraus ergibt sich eine Größe des Atomkerns in der Größenordnung von 10^-14Meter.

Rutherford stellt jedes Atom als Mini-Sonnensystem dar, in dessen Mitte sich der Kern befindet und die Elektronen wie Planeten umkreisen.

Seit dem Aufkommen der Quantenmechanik (1920er Jahre) ist das Bild des Kerns beunruhigend; Der Kern ist kein System mehr, das aus miteinander verbundenen Teilchen besteht. Der durch die Quantenmechanik gesteuerte Kern ist nicht beobachtbar, da man zur Beobachtung der Nukleonen im Inneren des Kerns die Teilchen mit so intensivem Licht beleuchten müsste, dass der Kern sofort zerfallen würde.

Das Gleiche gilt für das Elektron. Wir stellen das Elektron nicht mehr als ein Korpuskel dar, das sich in einer sehr regelmäßigen Umlaufbahn um den Kern dreht. Das Elektron ist weder eine Welle noch ein Korpuskel, wir sprechen jedoch vom Welle-Korpuskel-Dualismus, der die Grundlage der Quantenmechanik bildet. Das Elektron folgt keiner einzigen Flugbahn, es befindet sich wahrscheinlich in einer Region um den Kern, die Atomorbital genannt wird.

Elektronenwolke oder Atomorbital

Seit 1924 ist mit jeder Materie eine Welle verbunden, so die Hypothese vonLouis De Broglie(1892-1987). Mit dieser Hypothese verallgemeinert er auf alle Materieteilchen die „Welle-Teilchen-Dualität„Eingeführt für Licht, vonMax Planck(1858-1947) zu Beginn des 20. Jahrhunderts.

Alle subatomaren Teilchen haben daher eine Wellenlänge. Die Wellenlänge λ eines subatomaren Teilchens und sein Impuls p sind durch die Gleichung verknüpft: λ=h/p, wobei h das Plancksche Wirkungsquantum ist, p der Impuls, also das Produkt aus Masse und Geschwindigkeitsvektor (p=mv). Das Elektron benötigt etwa 150 Attosekunden (1,5×10⁻¹⁶Sekunden), um das Wasserstoffatom zu „umrunden“.

Dank Einsteins Formel (E=mc2) ist jeder Materie eine Energie zugeordnet. Mit anderen Worten: Je kleiner die Wellenlänge, desto höher die Energie (E=h/λ). Diese Energie wird die Form der Atome verändern. Anschließend werden die Grundlagen der Quantenmechanik gelegt.

Wie sehen Teilchen in der Welt des unendlich Kleinen aus?

Materie besteht aus sehr kleinen Teilchen (Elektronen, Neutrinos, Quarks), die eine Masse, eine Ladung, eine Energie, eine Dimension, eine Welle, einen Spin haben.

Im Jahr 2013 können wir noch immer nicht die Teilchen des Atomkerns sehen, sondern nur die äußere Schicht des Atoms, also seine Elektronenwolke. Die Elektronenwolke nimmt die gesamte räumliche Ausdehnung des Atoms ein, da sie etwa 10.000 Mal größer als sein Kern ist.

In der Wellenquantenmechanik wird ein Teilchen durch eine Wellenfunktion (Zustandsvektor) dargestellt, es ist jedoch sehr schwierig, das grundlegende Konzept der Quantenmechanik oder den Quantenzustand eines Systems darzustellen.

Im Jahr 1927Max Born(1882-1970) gaben eine Interpretation der Wellenfunktion, bei der das Quadrat der Wellenfunktion die Wahrscheinlichkeit darstellt, das Teilchen bei einer Messung an einem bestimmten Ort zu finden.

Eine Wellenfunktion ist daher eine Wahrscheinlichkeitsamplitude oder sogar eine Wahrscheinlichkeitsdichte für die Anwesenheit des Systems an einem bestimmten Ort zu einem bestimmten Zeitpunkt. Diese Funktion hat einen komplexen Wert. Wenn eine reelle Zahl oder ein reeller Wert beispielsweise die Länge einer Strecke auf einer Geraden darstellt, wird ein komplexer Wert durch einen Vektor in einer Ebene dargestellt. Dieser Vektor hat nicht nur eine Länge im Raum, sondern auch eine Phase, die der Richtung des Vektors entspricht.

Wenn wir das Elektron nicht mehr als Punktteilchen in einer regelmäßigen Umlaufbahn um einen Kern darstellen, wie können wir uns dann ein Bild davon machen?

Das Elektron folgt keiner einzigen Flugbahn um den Kern, es befindet sich irgendwo in einer „riesigen Region“, die Elektronenwolke oder Atomorbital genannt wird. Der Zustand eines Elektrons wird daher durch dieses Raumvolumen um den Kern herum dargestellt, in dem es delokalisiert ist. Der Grundzustand eines Wasserstoffatoms misst etwa 1 Angström oder 10^-10Meter.

Um sich das Elektron in dieser Region vorzustellen, genügt es, sich ein etwa 5 mm großes Reiskorn vorzustellen, das sich in einer Kugel von etwa 50 Metern Durchmesser bewegt. Aber es ist nicht immer eine Kugel, die Form dieses Bereichs des Atomraums hängt von der Energie des Elektrons und seinem Drehimpuls ab.

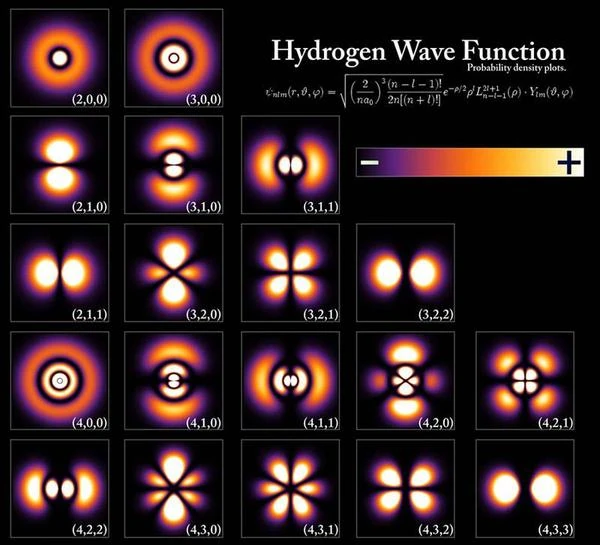
Die Orbitale des Elektrons können je nach Beschaffenheit des Atoms unterschiedliche charakteristische Formen annehmen, zum Beispiel hat das Orbital des Wasserstoffatoms in der ersten Reihe oben im Bild eine Kugelform, das Orbital in der zweiten Reihe hat die Form von zwei Wassertropfen, das Orbital in der dritten Reihe hat die Form von vier Wassertropfen. Zusammenfassend entspricht das Orbital dem Raumbereich, in dem das Elektron delokalisiert ist. Der Zustand des Elektrons befindet sich in einer Überlagerung aller möglichen Positionen innerhalb des Atomorbitals, deren Form variiert. Die Form des Orbitals ändert sich, wenn das Atom angeregt wird, wie in der ersten Reihe. Wenn wir das Atom noch stärker anregen, ändert sich die Form des Orbitals erneut wie in der zweiten Reihe oder zweiten Elektronenhülle. In einem sehr angeregten Zustand namens „Rydberg-Zustand“ sind die Elektronen in einem Torus mit „sehr großem Radius“, der bis zu 1000 Angström messen kann, delokalisiert, die Hauptquantenzahl n (Schalenzahl) liegt sehr hoch zwischen 50 und 100.

Hinweis: Ein Elektron, das von der positiven Ladung des Kerns angezogen wird, kann nicht „am Kern haften bleiben“, da dies bedeuten würde, dass sich die räumliche Ausdehnung seiner Wellenfunktion auf einen Punkt (ohne Geschwindigkeit und Drehimpuls) reduziert. Die Schrödinger-Gleichung besagt, dass sich ein Elektron in der Nähe des Kerns in einem Orbital befindet, dessen Geometrie durch die Quantenzahlen bestimmt wird, die diese Gleichung erfüllen. Kurz gesagt, ein Elektron wird durch den elektrostatischen Potentialtopf in der Nähe des Kerns gehalten. Wenn die potentielle Energie zunimmt, sagt man, dass sich das Teilchen in einem Potentialtopf bewegt.