原子軌道を理解する

画像の説明: ザ水素原子の原子軌道は電子のエネルギーと角運動量の関数として表されます。エネルギー準位は上から下 (n = 1、2、3、4、5) に増加し、角運動量は左から右に増加します (l = s、p、d、f、g)。 色： 黒: 確率密度がゼロ (電子がそこに行くことはありません)。 白: 最大密度 (電子が頻繁に通過します)。 オレンジレッド: 中間の濃度。 量子数: n: 主量子数。エネルギー準位を定義します。 l: 二次または軌道量子数。サブシェル (s、p、d、f、g...) を定義します。 m: 磁気量子数。軌道の方向を表します。 s: スピン量子数。電子の固有角運動量を定量化します。 この表現は、原子核の周囲のさまざまな領域で電子が見つかる確率密度を示しています。 画像の出典: GNU Free Documentation License。

原子の構造

科学者たちは（20世紀に）物質の最小構成要素に注目することによって、宇宙全体の機能を説明することになる。

原子は原子核で構成され、その周りを 1 つまたは複数の電子が動きます。 原子核を特徴付けるのは、1 ～ 110 の範囲の陽子数 (Z) です。これが元素を決定します。たとえば、鉄 (Fe26) には 26 個の陽子があり、26 がその原子番号 (Z) です。 0 ～ 160 の範囲の中性子 (N) の数は、元素の同位体を特徴付けます。たとえば、水素 (H1) には陽子が 1 つあり中性子はありません。重水素 (H2) には陽子が 1 つと中性子が 1 つあり、三重水素 (H3) には陽子が 1 つと中性子が 2 つあります。

これらの 3 つの形態の水素には、電荷が 1 つしかないため、電子が 1 つだけあります。つまり、単一の陽子です。

水素の場合のみ、元素の同位体に別の名前が付けられており、他のすべての場合は、中性子の数を見つけることができる核子の数のみを示すことに注意してください。 たとえば、鉄 (Fe26) には Fe56 を含むいくつかの同位体があり、Fe56 には 30 個の中性子があり、Fe57 には 31 個の中性子があり、Fe58 には 32 個の中性子があり、中性子の数によって同位体が明確に区別されます。

原子の中で、物質に一貫性を与えているのは電子ですが、それは非常に軽い (≈10^-27g)。 陽子は約 2000 倍重く、原子の質量の大部分 (99.99%) が集中します。 安定した原子の場合、質量は 1.674×10 の間になります。^-24水素の場合は g、3.953×10^-22ウランの場合はg。

1811 年以来、原子のおおよそのサイズもわかっています。アメデオ・アボガドロ(1776-1856) 原子の大きさは 10-10 メートル (オングストローム)、つまり 1000 万分の 1 ミリメートル強と推定されました。 1911年に、アーネスト・ラザフォード(1871-1937) 原子核を発見しました。

ラザフォードは、ウランの放射性崩壊から生じる粒子を金シートに衝突させることにより、原子の構造を明らかにしました。 原子核の大きさは 10 程度になります。^-14メーター。

ラザフォードは、各原子を小さな太陽系として表し、中心に原子核があり、惑星のように周回する電子があります。

量子力学の出現（1920年代）以来、原子核のイメージは不安を与えるものとなってきました。核はもはや、結合した小体から構成されるシステムではありません。 量子力学が支配する原子核は観測できません。原子核内の核子を観察するには、原子核が瞬時に崩壊してしまうほど強い光を粒子に照射する必要があるからです。

これは電子についても同じであり、電子を原子核の周りを非常に規則的な軌道で回転する微粒子として表すことはなくなりました。 電子は波でも粒子でもありませんが、ここでは量子力学の基礎である波と粒子の二重性について話しています。 電子は単一の軌道をたどるのではなく、おそらく原子軌道と呼ばれる原子核の周りの領域に位置しています。

電子雲または原子軌道

1924 年以来、すべての物質には波動が関連付けられている、これが次の仮説です。ルイ・ド・ブロイ（1892-1987）。 この仮説により、彼は物質のすべての粒子に一般化します。波動粒子双対性「光のために導入された、マックス・プランク(1858-1947) 20 世紀初頭。

したがって、すべての亜原子粒子には波長があります。 素粒子の波長 λ とその運動量 p は、方程式 λ=h/p で関連付けられます。ここで、h はプランク定数、p は運動量、つまり質量と速度ベクトルの積 (p=mv) です。 電子は約 150 アト秒 (1.5×10⁻¹⁶秒）水素原子を「一周」します。

アインシュタインの公式 (E=mc2) のおかげで、すべての物質は関連するエネルギーを持っています。 言い換えれば、波長が短いほどエネルギーは高くなります（E=h/λ）。 このエネルギーは原子の形状を変化させます。 その後、量子力学の基礎が築かれます。

無限に小さい世界の粒子はどのように見えるのでしょうか？

物質は、質量、電荷、エネルギー、寸法、波動、スピンを持つ非常に小さな粒子 (電子、ニュートリノ、クォーク) で構成されています。

2013年現在、私たちはまだ原子核の粒子を見ることはできず、原子の外層、つまり電子雲しか見ることができません。 The electron cloud occupies the entire spatial extent of the atom since it is approximately 10,000 times larger than its nucleus.

波動量子力学では粒子は波動関数（状態ベクトル）で表現されますが、量子力学の基本概念や系の量子状態を表現することは非常に困難です。

1927年に、マックス・ボーン(1882-1970) は、波動関数の解釈を与えました。波動関数の 2 乗は、測定が行われたときに特定の場所で粒子が見つかる確率を表します。

したがって、波動関数は、特定の時間における特定の位置におけるシステムの存在の確率振幅、または確率密度ですらあります。 この関数は複素数値を持ちます。 たとえば、実数または実数値が直線上の線分の長さを表す場合、複素数値は平面内のベクトルで表されます。 このベクトルは空間内での長さだけでなく、ベクトルの方向に対応する位相も持ちます。

電子を原子核の周りを規則正しく周回する点粒子として表現できなくなったら、どうやって電子の像を形成できるのでしょうか?

電子は原子核の周りを単一の軌道をたどるのではなく、電子雲または原子軌道と呼ばれる「広大な領域」のどこかに位置しています。 したがって、電子の状態は、電子が非局在化している原子核の周囲の空間の体積によって表されます。 The ground state of a hydrogen atom measures approximately 1 angstrom or 10^-10メーター。

この領域の電子を想像するには、直径約 50 メートルの球内を移動する約 5 mm の米粒を想像するだけで十分です。 しかし、それは常に球であるわけではなく、原子空間のこの領域の形状は電子のエネルギーとその角運動量に依存します。

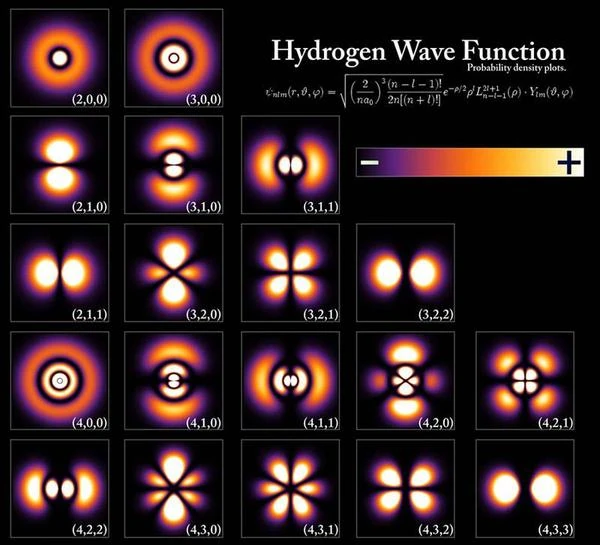
電子の軌道は、原子の性質に応じてさまざまな特徴的な形状をとることができます。たとえば、画像の上部の 1 行目の水素原子の軌道は球形、2 行目の軌道は 2 つの水滴の形状、3 行目の軌道は 4 つの水滴の形状です。 要約すると、軌道は電子が非局在化されている空間領域に対応し、電子の状態は形状が変化する原子軌道内のすべての可能な位置を重ね合わせたものになります。最初の行のように、原子が励起されると軌道の形状が変化します。原子をさらに励起すると、軌道の形状は再び第 2 列または第 2 電子殻のように変化します。 「リュードベリ状態」と呼ばれる非常に励起された状態では、電子は最大 1000 オングストロームの「非常に大きな半径」のトーラス内に非局在化し、主量子数 n (シェル数) は 50 ～ 100 と非常に高くなります。

注: 原子核の正電荷に引き寄せられた電子は、「原子核にくっつく」ことができません。これは、その波動関数の空間的広がりが (速度や角運動量なしで) 点まで縮小されることを意味するからです。シュレーディンガー方程式によれば、原子核の近くにある電子は、この方程式を満たす量子数によって決定される幾何学的軌道にあるとされています。つまり、電子は静電ポテンシャル井戸によって原子核の近くに閉じ込められます。ポテンシャルエネルギーが増加すると、粒子はポテンシャル井戸内を移動するといわれます。