最終更新日: 2024 年 10 月 26 日

ブラウン運動: なぜ粒子は勝手に動くのでしょうか?

ロバート・ブラウンによるブラウン運動: 偶然か物理法則か?

ロバート・ブラウン(1773-1858) スコットランドの植物学者、友人チャールズ・ダーウィン(1809 - 1882) は 1827 年に、水中に浮遊する花粉粒を顕微鏡で観察することにより、花粉粒が静止しておらず、明白な理由もなく常に不規則に移動していることを発見しました。この動きが生きた花粉に特に関連していないことを確認するために、ブラウン氏は塵の破片や非常に小さな無機粒子などの無生物を使った実験を繰り返した。非常に驚いたことに、これらの不活性粒子も同じランダムな動きを示すことを発見しました。ブラウンはこの現象を正確に記録しましたが、その起源については理解していませんでした。

何十年にもわたって、多くの物理学者は、すべての測定バイアス（室内の気流、花粉粒が存在する水の中の流れ、振動、光による妨害など）を取り除き、ますます効率の高い顕微鏡を使用して実験を繰り返してきましたが、誰もこの自然な撹拌の説明を見つけていません。

19世紀の分子動力学理論

そこには分子動力学理論そのルーツは 19 世紀の科学者の研究にあります。これは主に 3 人の主要な物理学者によって定式化および開発されました。ルドルフ・クラウジウス(1822-1888)、ジェームズ・クラーク・マクスウェル(1831-1879) とルートヴィヒ・ボルツマン（1844-1906）。

分子動力学理論は、「分子」または「微粒子」と呼ばれる非常に小さな粒子の観点から物質の巨視的特性を説明するモデルを提案しました。当時、原子の概念はまだ実験的に証明されていませんでしたが、科学者たちは、次のような現象を説明するために、小さな目に見えない実体の存在を仮定しました。プレッシャー、そこには温度そして気体状態。

運動理論は、すべての物質は絶えず運動する実体で構成されているという考えに基づいています。この時点では、原子の存在についてはまだ議論の余地がありましたが、科学者たちはこれらの粒子のアイデアが観察可能な現象を説明するのに役立つと考えました。たとえば、ガスによって加えられる圧力は、ガス粒子が容器の壁に絶え間なく衝突することによって発生します。粒子の数が多く、粒子の速度が速いほど、圧力は増加します。温度は、移動する粒子の平均運動エネルギーに比例すると解釈されます。したがって、より高温のガスには、より速く移動する粒子が含まれています。

原子の存在が確認されない限り、分子動力学理論は抽象的なモデルのままでした。分子が運動しているという考えは、一部の人には数学的な説明として受け入れられましたが、他の科学者は依然として懐疑的であり、これらの粒子を直接の実験的根拠のない仮説上の存在と見なしていました。

アインシュタインと撹拌粒子の謎

1905 年、原子と分子の物理的実在性がより広範に検証され、分子動力学理論に強固な基盤が提供されました。の記事アルバート・アインシュタイン、1905年5月11日に出版された「熱の分子運動理論が示唆する静止流体中に懸濁された粒子の運動について」と題された論文はブラウン運動を扱っている。アインシュタインは、ブラウン運動を、分子運動の観点から気体や液体の特性を説明する分子運動理論に結び付けようとしました。

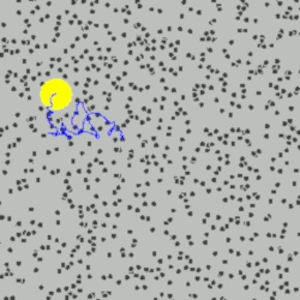
アインシュタインは、ブラウン運動において、浮遊した塵が周囲の流体の分子によって継続的に衝突されるという考えから出発しました。塵の動きは、ランダムではあるが一定の方法で作用するこれらの分子の不均衡な衝撃によって引き起こされます。

アインシュタインは、このランダムな動きを定量的に説明する方程式を開発しました。これは、平均粒子変位を時間、流体温度、流体粘度、および粒子 (花粉) サイズに関連付けます。

そこには数学的モデリングは ⟨x2⟩ = 2kB Tt/6πηr ここで、⟨x2⟩ は時間 t 後に粒子 (花粉) が移動する二乗平均平方根距離、�� はボルツマン定数、�� は流体の絶対温度、�� は流体の粘度、�� は粒子の半径です。これ方程式微視的な特性（分子の熱撹拌など）を巨視的な観察（花粉やその他の粒子の観察可能な動き）に結び付けます。

原子の存在の予測と証明

アインシュタインは、ブラウン運動により、当時まだ議論されていた原子や分子の存在を実験的に検証できることを実証しました。観察された粒子の動きは、分子動力学理論によって予測されたものと正確に一致します。アルバート・アインシュタインは論文の中で原子の大きさを直接決定していませんが、物質の原子の性質を探ることを可能にする基礎を確立しています。

ジャン・ペランフランスの物理学者（1870-1942）は、1908 年から 1909 年にかけてアインシュタインの予測を検証するために一連の実験を実施しました。ペリン氏は、水中に浮遊した樹脂粒子の動きを顕微鏡で測定することで、その結果がアインシュタインの計算と一致することを観察し、粒子の動きと分子衝突の関係を確認しました。

ブラウン運動: 2 つの世界の間のつながり

微視的なスケールでは、ブラウン運動は、急速かつ無秩序に移動する目に見えない分子 (水分子のような) 間の相互作用によって引き起こされます。これらの分子は浮遊粒子と相互作用し、一見ランダムな動きをもたらします。巨視的レベルでは、ブラウン運動は浮遊粒子の挙動を通じて肉眼（顕微鏡）で観察できます。たとえば、花粉粒が水滴の中で不規則に動いているのが見られます。

要約すると、ブラウン運動は、ミクロの世界そして巨視的な世界。これは、原子および分子スケールでの出来事が、より大きなスケールでの測定可能かつ予測可能な挙動にどのように変換されるかを示し、さまざまなレベルでの物理現象の理解を強化します。