最終更新日: 2025 年 10 月 11 日

量子の重ね合わせ: 亜原子世界の中心

量子重ね合わせの表現 — 干渉はすべての量子粒子に関係します。それらは、電子、光子、中性子、原子、さらには分子とともに観察されています。波の特徴であるこれらの現象は、実験的には微視的なスケールで現れますが、古典的な巨視的な世界では消えてしまいます。同じタイプの伝播 (機械的、電磁波、音響など) の 2 つの波が重なり合うことがあり、それが私たちが観察するような干渉パターンを引き起こします。
画像出典:ウィキメディア・コモンズ

レイヤリング

定義と原則

そこには量子状態の重ね合わせこれは、測定が行われるまで粒子が複数の可能な状態で同時に存在できるという量子力学の基本原理です。この現象を理論化したものは、エルヴィン・シュレディンガー(1887-1961) およびその他の 20 世紀の先駆者は、亜原子システムの本質的に確率論的で非決定論的な性質を強調しています。

確率波とそれに伴う現象

重ね合わせ状態では、確率波の各成分が粒子の全体的なダイナミクスに寄与し、その結果、干渉やもつれ現象が発生する可能性があります。巨視的スケールでは目に見えないこれらの効果は、量子システムの集合的な動作を理解するために不可欠となり、量子コンピューティング、超高精度センサー、量子暗号などの新興技術の理論的基礎を構成します。

波動関数と崩壊

重ね合わせは次の概念も示します。波動関数これは、観測中の量子システムの複数の状態から単一の状態への遷移を説明し、微視的な現実と巨視的な経験の根本的な違いを強調しています。

物理的特性と影響

量子の効果と測定

重ね合わせ状態では、確率波の各成分が量子システムの全体的なダイナミクスに影響を与えます。観察または測定により、波動関数の崩壊、システムが可能な状態の中から単一の測定可能な状態を強制的に採用します。このメカニズムは、量子力学の本質的な確率的性質と古典的なシステムとの根本的な違いを示しています。

巨視的な現象と一貫性

重ね合わせは多くの量子現象の中心です。もつれ、いくつかの粒子が非局所的に相関するようになり、干渉顕微鏡スケールで観察されます。また、量子コンピューティング、超高精度原子時計、高感度磁場センサーや重力場センサーなどの新興テクノロジーの動作に必要な条件である量子コヒーレンスも可能になります。

哲学的かつ基本的な意味合い

重ね合わせの基本的な意味は、純粋に実験的なものを超えており、亜原子世界における現実、測定、観察の性質について深い疑問を投げかけます。

実験方法と技術

実験と観察

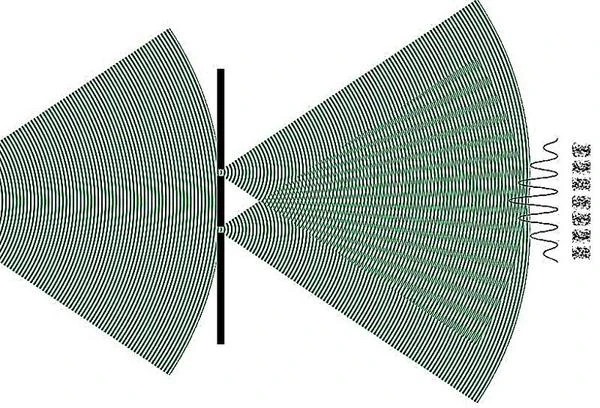
量子状態の重ね合わせは、高度な実験のおかげで明らかになります。干渉計レーザーによって捕捉され冷却された光子、電子、中性子、または超低温原子を使用します。これらの実験により、干渉パターンを直接観察することが可能になり、複数の量子状態が同時に共存していることが明らかになりました。

技術応用

重ね合わせを利用するテクノロジーは量子コンピューティングの中心であり、量子ビットが 0 と 1 を同時に表現できるため、特定のタスクのコンピューティング能力が飛躍的に向上します。また、量子コヒーレンスを利用して比類のない精度で時間を計測する超高精度原子時計も含まれています。量子暗号、もつれと重ね合わせの特性により、改ざん防止通信が保証されます。

重要性と展望

これらの実験方法と技術的応用は、量子重ね合わせが単なる理論的現象ではなく、最先端技術の開発と量子物理学の限界の探求のための基本的なリソースを構成することを示しています。

量子状態の比較表

量子状態と古典状態の比較
ステータスの種類	主な特長	例	アプリケーション
古典的な状態	決定的、測定可能	ボールの位置、車の速度	ニュートン物理学、機械工学
量子状態	複数の状態のオーバーレイ	電子のスピン、原子内の電子の位置	干渉法、量子センサー、量子コンピューティング
量子もつれ	分離した粒子間の瞬時相関	もつれた光子のペア、もつれた電子	量子暗号、量子テレポーテーション、量子ネットワーク
一貫した状態	量子ゆらぎの最小限の重ね合わせ	レーザー、量子調和発振器	量子光学、量子通信、計測学
純粋な状態	波動関数に関する完全な知識	孤立した原子の基底状態	量子シミュレーション、量子計算、基礎実験
混合状態	純粋状態の統計的混合	有限温度の原子系	量子熱力学、デコヒーレンス、量子センサー
定常状態	確率に時間的変化はない	水素原子のエネルギー準位	分光法、原子時計
興奮状態	基底状態以上のエネルギー	原子の高次レベルにある電子	発光、レーザー、分光法
基底状態	可能な限り最小限のエネルギー	最下位の電子	原子の安定性、原子時計のリファレンス

量子重ね合わせは、古典的な規則がもはや適用されず、現実は測定されるまでポテンシャルの状態で存在しているように見える、素粒子物理学の特異点を示しています。この概念は、量子コンピューティングと高度な量子技術における現代の研究の中心です。