Atome : Orbitales Atomiques

Description de l'image : Les orbitales atomiques de l'atome d'hydrogène sont représentées en fonction de l'énergie de l'électron et de son moment cinétique. Le niveau d'énergie augmente de haut en bas (n = 1, 2, 3, 4, 5) et le moment cinétique augmente de gauche à droite (l = s, p, d, f, g). Couleurs : Noir : densité de probabilité nulle (l'électron n'y va jamais). Blanc : densité maximale (l'électron y passe souvent). Rouge orangé : densité intermédiaire. Nombres quantiques : n : nombre quantique principal, définit le niveau d'énergie. l : nombre quantique secondaire ou orbital, définit les sous-couches (s, p, d, f, g...). m : nombre quantique magnétique, représente les orientations des orbitales. s : nombre quantique de spin, quantifie le moment cinétique intrinsèque de l'électron. Cette représentation montre la densité de probabilité de trouver l'électron dans différentes zones autour du noyau. Source image : GNU Free Documentation License.

Structure de l'atome

C'est en regardant les plus petits constituants de la matière que les scientifiques vont expliquer (20è siècle) le fonctionnement de l'univers tout entier.

Un atome est constitué d'un noyau autour duquel se déplace un ou plusieurs électrons. Ce qui caractérise le noyau est son nombre de protons (Z) qui va de 1 à 110, c'est lui qui détermine l'élément, exemple le fer (Fe26) a 26 protons, 26 est son numéro atomique (Z). Le nombre de neutrons (N) qui va de 0 à 160, caractérise les isotopes de l'élément, par exemple, l'hydrogène (H1) a un proton et aucun neutron, le deutérium (H2) a un proton et un neutron, le tritium (H3) a un proton et deux neutrons.

Ces trois formes de l'hydrogène n'ont qu'un seul électron puisqu'il n'y a qu'une seule charge électrique, l'unique proton.

Attention, il n'y a que dans le cas de l'hydrogène que l'on donne un nom différent aux isotopes de l'élément, dans tous les autres cas on indique seulement le nombre de nucléons ce qui permet de retrouver le nombre de neutrons. Par exemple le fer (Fe26) a plusieurs isotopes dont Fe56, on comprend que Fe56 a 30 neutrons, Fe57 a 31 neutrons, Fe58 a 32 neutrons, le nombre de neutrons différencie bien les isotopes.

Dans l'atome ce sont les électrons qui donnent sa consistance à la matière, pourtant il est très léger (≈10^-27 g). Le proton est ≈2000 fois plus lourd et concentre l'essentiel de la masse de l'atome (99,99%). Pour les atomes stables, la masse est comprise entre 1,674×10^-24 g pour l'Hydrogène et 3,953×10^-22 g pour l'uranium.

Depuis 1811, on connait aussi la taille approximative d'un atome, Amedeo Avogadro (1776-1856) a estimé la taille des atomes à 10-10 mètre (Angstrom), c'est-à-dire un peu plus de 10 millionième de millimètre. En 1911, Ernest Rutherford (1871-1937) découvre le noyau atomique.

Rutherford précise la structure de l'atome en bombardant une feuille d'or avec des particules issues de la désintégration radioactive de l'uranium. Il donne une taille au noyau atomique de l'ordre de 10^-14 mètre.

Rutherford représente chaque atome comme un mini système solaire, au centre le noyau et en orbite comme des planètes, les électrons.

Depuis l'avènement de la mécanique quantique (décennie 1920) l'image du noyau est troublante, le noyau n'est plus un système composé de corpuscules associées ensemble. Le noyau régit par la mécanique quantique n'est pas observable car pour observer les nucléons à l'intérieur du noyau, il faudrait éclairer les particules avec une lumière tellement intense que le noyau se désintègrerait instantanément.

Il en est de même pour l'électron, on ne représente plus l'électron comme un corpuscule qui tourne sur une orbite bien régulière autour du noyau. L'électron n'est ni une onde ni un corpuscule, cependant on parle de la dualité onde-corpuscule qui est le fondement de la mécanique quantique. L'électron ne suit pas une trajectoire unique, il se situe probablement dans une région autour du noyau que l'on appelle l'orbitale atomique.

Nuage Electronique ou Orbitale Atomique

Depuis 1924, toute matière est dotée d'une onde associée, c'est l'hypothèse de Louis De Broglie (1892-1987). Avec cette hypothèse, il généralise à toute les particules de la matière, la "dualité onde-particule" introduite pour la lumière, par Max Planck (1858-1947) au début du 20è siècle.

Toutes les particules subatomiques ont donc une longueur d'onde. La longueur d'onde λ d'une particule subatomique et sa quantité de mouvement p sont reliées par l'équation : λ=h/p, où h est la constante de Planck, p la quantité de mouvement c'est-à-dire le produit de la masse par le vecteur vitesse (p=mv). L'électron met environ 150 attosecondes (1.5×10⁻¹⁶ secondes) pour "faire le tour" de l'atome d'Hydrogène.

Grâce à la formule d'Einstein (E=mc2) toute la matière est dotée d'une énergie associée. En d'autres termes, plus la longueur d'onde est petite, plus l'énergie est élevée (E=h/λ). Cette énergie va modifier la forme des atomes. Les bases de la mécanique quantique sont alors posées.

A quoi ressemblent les particules du monde de l'infiniment petit ?

La matière est composée de particules très petites (électrons, neutrinos, quarks) qui ont une masse, une charge, une énergie, une dimension, une onde, un spin.

En 2013 nous ne pouvons toujours pas voir les particules du noyau atomique mais seulement la couche extérieure de l'atome i.e. son nuage électronique. Le nuage électronique occupe toute l'étendue spatiale de l'atome puisqu'il est environ 10 000 fois plus grand que son noyau.

En mécanique quantique ondulatoire, une particule est représentée par une fonction d'onde (vecteur d'état) mais il est très difficile de se représenter le concept fondamental de la mécanique quantique ou l'état quantique d'un système.

En 1927, Max Born (1882-1970) a donné une interprétation de la fonction d'onde où le carré de la fonction d'onde représente la probabilité de trouver la particule en un endroit précis, quand on fait une mesure.

Une fonction d'onde est donc une amplitude de probabilité ou encore une densité de probabilité de présence du système dans une position donnée, à un instant donné. Cette fonction a une valeur complexe. Si un nombre réel ou une valeur réelle représente, par exemple, la longueur d'un segment sur une droite, une valeur complexe est représentée par un vecteur dans un plan. Ce vecteur a non seulement une longueur dans l'espace mais aussi une phase qui correspond à la direction du vecteur.

Si on ne représente plus l'électron comme une particule ponctuelle sur une orbite régulière autour d'un noyau, comment peut-on s'en faire une image ?

L'électron ne suit pas une trajectoire unique autour du noyau, il se situe quelque part dans une "vaste région" que l'on appelle le nuage électronique ou orbitale atomique. L'état d'un électron est donc représenté par ce volume de l'espace autour du noyau dans lequel il est délocalisé. L'état fondamental d'un atome d'hydrogène mesure environ 1 angström soit 10^-10 mètre.

Pour se représenter l'électron dans cette région il suffit d'imaginer un grain de riz d'environ 5 mm se déplacer dans une sphère d'environ 50 mètres de diamètre. Mais ce n'est pas toujours une sphère, la forme de cette région de l'espace atomique dépend de l'énergie de l'électron et de son moment cinétique.

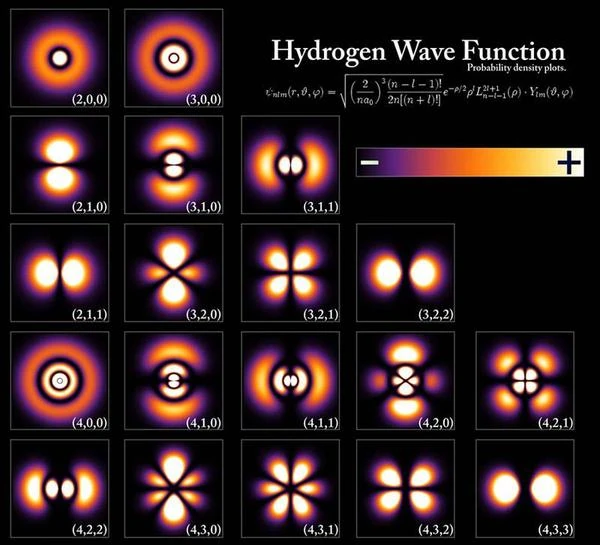
Les orbitales de l'électron peuvent prendre différentes formes caractéristiques en fonction de la nature de l'atome, par exemple l'orbitale de l'atome d'hydrogène sur la première rangée en haut de l'image, a une forme sphérique, l'orbitale sur la deuxième rangée a la forme de deux gouttes d'eau, l'orbitale sur la troisième rangée a la forme de quatre gouttes d'eau. En résumé, l'orbitale correspond à la région de l'espace où l'électron est délocalisé, l'état de l'électron est dans une superposition de toutes les positions possibles à l'intérieur de l'orbitale atomique dont la forme varie. La forme de l'orbitale change lorsqu'on excite l'atome, comme sur la première rangée. Si l'on excite encore plus l'atome, la forme de l'orbitale change à nouveau comme sur la deuxième rangée ou deuxième couche électronique. Dans un état très excité appelé "état de Rydberg", les électrons sont délocalisés dans un tore de « très grand rayon » qui peut mesurer jusqu'à 1000 angströms, le nombre quantique principal n (numéro de la couche) est très élevé entre 50 et 100.

N. B. : Un électron, attiré par la charge positive du noyau, ne peut pas "coller au noyau" car cela signifierait que l'extension spatiale de sa fonction d'onde est réduite à un point (sans vitesse ni moment cinétique). L'équation de Schrödinger dit qu'un électron, au voisinage du noyau, se trouve dans une orbitale à la géométrie déterminée par les nombres quantiques qui satisfont cette équation. En bref, un électron est confiné dans le voisinage du noyau par le puits de potentiel électrostatique. Lorsque l'énergie potentielle est croissante, on dit que la particule se meut dans un puits de potentiel.