Dernière mise à jour 4 décembre 2021

E=mc² : une Equation, une Révolution

Relativité Restreinte : Bien plus qu'une Formule Célèbre

E=mc2 est l'équation la plus connue et la plus vulgarisée de toute la physique.

L'équation E=mc2 apparaît pour la première fois dans l'article d'Albert Einstein intitulé "L'inertie d'un corps dépend-elle de l'énergie qu'il contient ?", publié dans le journal Annalen der Physik le 27 septembre 1905. Elle apparait après l'article du 30 juin 1905 intitulé "Sur l'électrodynamique des corps en mouvement". Cet article de juin 1905 contient la base de ce que l'on appellera ensuite "La Théorie de la Relativité Restreinte".

La théorie de la relativité restreinte repose sur deux principes : la relativité galiléenne et l'invariance de la vitesse de la lumière. La relativité galiléenne dit que les lois de la physique restent inchangées dans des référentiels d'inertie (systèmes de référence en mouvement uniforme) dénommés depuis référentiels galiléens. De plus la vitesse est relative par rapport à un repère, un point choisi arbitrairement comme fixe. L'invariance de la vitesse de la lumière implique que c'est une vitesse limite et indépassable, quel que soit le référentiel.

Mais que veut dire exactement l'équation E=mc2 ?

En réalité, l'équation originale est E2=m2c4+p2c2. (E=énergie, m=masse, c=vitesse de la lumière, p=impulsion ou quantité de mouvement). En d'autres termes l'énergie totale d'un corps est la somme de son énergie de masse au repos (m2c4) plus son énergie cinétique (p2c2).

Si un corps est immobile, son impulsion est nulle alors E2=m2c4 ⇒ E=mc2. Autres formes de l'équation m=E/c2 ou Δm=ΔE/c2 (Δ=variation).

Cette équation E=mc2 a d'énormes conséquences sur les concepts d'espace, de temps, de masse et d'énergie mais aussi sur la physique de l'infiniment grand (cosmologie) et de l'infiniment petit (physique quantique).

N. B. : Loi de composition des vitesses : Si V1 est la vitesse du référentiel R1 (par exemple un train qui roule à 100 km/h) et V2 est la vitesse d'un marcheur (référentiel R2) qui se déplace à 10 km/h dans le même sens que le train par rapport au train, à quelle vitesse V0 se déplace le marcheur par rapport au quai (référentiel R0) ? La réponse est V0 = V1+V2=110 km/h. Du point de vue du quai le train se déplace à 100 km/h et le marcheur à 110 km/h. Du point de vue du train le marcheur se déplace à 10 km/h et le quai à -100 km/h. Du point de vue du marcheur le train se déplace à -10 km/h et le quai à -110 km/h. La vitesse est relative, elle dépend du point de vue. Aucune expérience de mécanique à l'intérieur du référentiel inertiel ne peut permettre de déterminer la vitesse de son propre référentiel.

N. B. : L'impulsion ou la quantité de mouvement transmise à un objet, est le produit de la masse par la vitesse (p=mv). Cela correspond à l'inertie de l'objet ou la difficulté à modifier son mouvement.

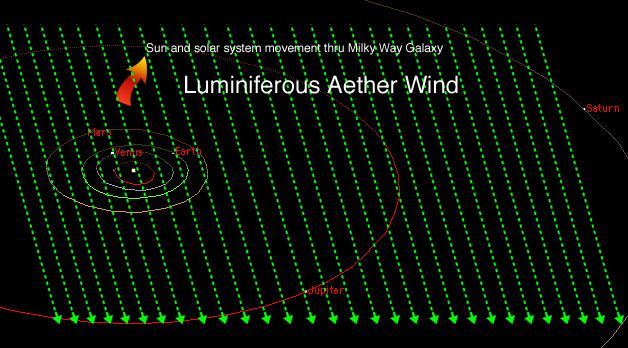
Éther Luminifère : Quand la Lumière Voyageait dans l'Éther

Dans l'article du 30 juin 1905 paru dans Annalen der Physik "Sur l'électrodynamique des corps en mouvement", Einstein postule que la lumière n'est pas seulement ondulatoire mais qu'elle est constituée de photons (corpuscules de lumière). Cela va lui permettre de remettre en cause l'existence de l'éther.

La lumière redéfinie par Maxwell est considérée depuis le 17è siècle comme une onde. Le son pour se propager a besoin d'un milieu (l'air) qui vibre au passage du son. De même une vague pour se propager a besoin d'un milieu (l'eau). Les physiciens du 18è siècle inventent alors l'éther luminifère, substrat immatériel qui sert de support dans le vide pour véhiculer la lumière. L'éther qui vibre au passage de la lumière fait consensus dans le monde scientifique. Pour Einstein, si la lumière n'est pas seulement ondulatoire, mais aussi constituée de photons, alors il n'y a pas besoin d'éther luminifère.

Einstein rejeta énergiquement le caractère stationnaire de l'éther défendu par Lorentz car cela était contraire au principe de relativité. La lumière peut se propager dans le vide comme des corpuscules.

N. B. : Selon les équations de James Clerk Maxwell (1831-1879), la lumière est une onde transversale électromagnétique auto-propageante avec des composantes électriques et magnétiques où les champs électriques et magnétiques oscillent à angle droit les uns par rapport aux autres et se propagent perpendiculairement à la direction dans laquelle ils se déplacent indéfiniment à moins d'être absorbés par la matière intermédiaire. Autrement dit, chaque type de champ - électrique et magnétique - génère l'autre afin de propager l'ensemble de la structure composite dans l'espace vide à la vitesse finie de la lumière, c (du latin celeritas "vitesse").

Vitesse de la Lumière : La Limite Ultime de la Nature

L'élimination de l'éther nous dit que la notion de vitesse absolue n'existe pas, la vitesse est relative. Ce qui implique que si un objet a une vitesse c dans un référentiel, alors il a une vitesse c dans tous les référentiels.

Comment accepter cette bizarrerie ?

Les postulats suivants sont nécessaires pour comprendre la théorie de la relativité restreinte.

Il n'y a pas de point privilégié dans l'espace et dans le temps, l'espace-temps est homogène. Si on fait une expérience les mesures resteront valables ici et là, hier et demain.
Il n'y a pas de direction privilégiée dans l'espace (l'espace est isotrope). Si on fait une expérience les mesures resteront valables dans toutes les directions de l'espace contrairement au temps qui va toujours dans le même sens (du passé vers le futur).
Les mêmes lois de transformation permettent de relier les mesures des expériences vues par des observateurs situés dans différents référentiels d'inertie.
Si un évènement A est la cause d'un évènement B, quelque soit l'observateur, l'évènement A sera toujours la cause de l'évènement B. La causalité doit être respectée c'est-à-dire que l'ordre des évènements ne sera jamais inversé quelque soit le mouvement.

Si on accepte ces postulats, les transformations de Lorentz (1853-1928) modifient la loi de composition des vitesses.

V=V1+V2 devient V=V1+V2 /1 + V1V2/c2

On démontre que si V2=c ⇒ V=c. L'énergie de V2 étant maximale, la vitesse V1 est nulle !

V=V1+c/1+V1c/c2=V1+c/1+V1/c=cV1+c/c+V1=c

c est devenu une constante limite et les objets qui se déplacent à la vitesse c ne dépendent pas du référentiel. Si un objet se propage à la vitesse de la lumière, alors il se propagera à la vitesse de la lumière pour tous les observateurs. L'expérience donne c=299 792 458 m/s. A notre échelle, V1 et V2 sont petits par rapport à c alors le facteur de Lorentz (γ=1/√1-v2/c2) très proche de 1, nous permet de retrouver V≈V1+V2.

Le facteur de Lorentz est le facteur de proportionnalité par lequel le temps, les longueurs et la masse relativistes changent pour un objet tandis que cet objet est en mouvement. Ce facteur prend une valeur infinie lorsque la vitesse de l'objet atteint la vitesse de la lumière.

γ=1/√1-v2/c2 ⇒ γ=1/√1-c2/c2 soit γ=1/0 =∞

La courbe représentative du facteur de Lorentz montre une asymptote. Cette asymptote monte subitement à la verticale lorsque v tend vers c. Voici quelques valeurs du facteur de Lorentz correspondant à différentes valeurs de la vitesse.

A 10% de c le facteur γ=1.005
A 20% de c le facteur γ=1.021
A 50% de c le facteur γ=1.16
A 99% de c le facteur γ≈7
A 99,9% de c le facteur γ≈22
A 99,99% de c le facteur γ≈71
A 100% de c le facteur gamma est infini.

Dilatation du Temps : L'impact de la vitesse et de la gravité

Le facteur de Lorentz (γ=1/√1-v2/c2) s'applique à tous les concepts dans un cadre relativiste et bien sûr le temps est concerné.

Un rayon laser qui se réfléchit sur la Lune met 1,3 s à l'aller et 1,3 s au retour. Le va et vient du mouvement du rayon laser qui voyage entre 2 miroirs peut être considéré comme une horloge. Un pilote qui passe à très grande vitesse à côté de la Terre observe un phénomène étrange. Il voit la lumière se déplacer dans un aller-retour non pas à la verticale mais en zigzag. Le rayon parcoure une distance plus longue pour lui que pour un observateur sur Terre. La direction du laser vue de l'observateur au sol est verticale donc la distance est plus courte que celle vue par le pilote.

Or v=dt et la vitesse de la lumière est invariante.Si v est invariant et la distance d plus grande alors le temps est plus court. Du point de vue du pilote le pendule de lumière oscille plus lentement que pour l'observateur sur Terre.

Dans le vaisseau spatial, le temps se dilate d'un facteur γ qui est fonction de la vitesse du vaisseau. Le mouvement provoque un ralentissement du temps. Cela a été démontrée de manière pratique avec des horloges atomiques qui permettent des mesures extrêmement précises. Deux horloges atomiques, l'une installée dans un avion en vol et l'autre placée sur terre, obtiennent des mesures du temps différentes. Il y une désynchronisation des horloges. L'horloge de l'avion est plus lente de quelques nanosecondes, mais la différence est réelle et mesurable. Cette infime différence tient à la faible vitesse de l'avion par rapport à la vitesse de la lumière.

Contraction des Longueurs : Un Effet Relativiste Fondamental

Le facteur de Lorentz (γ=1/√1-v2/c2) s'applique à tous les concepts dans un cadre relativiste. Les longueurs aussi sont concernées.

Pour mesurer la longueur d'un objet en mouvement il faut mesurer ses extrémités simultanément (exactement au même moment). Cela n'est pas possible pour un objet allant à la vitesse de la lumière. Pour pouvoir le mesurer, il faut qu'il soit immobile. Il faut donc se situer dans son propre référentiel où l'objet est immobile.

Dans son référentiel, la longueur des objets en mouvement est réduite par un facteur gamma. Pour comprendre ce phénomène de contraction des longueurs, un exemple sera plus explicite que des équations.

Les muons sont des particules élémentaires de charge électrique négative, instables, produites dans la haute atmosphère à 35 km d'altitude. Les rayons cosmiques sont des flux de noyaux atomiques (des protons) de haute énergie relativiste, venant de l'espace. Lorsque les rayons cosmiques percutent les atomes d'oxygène ou d'azote de la haute atmosphère, ils produisent des gerbes de particules dont des muons. Les muons ont une durée de vie est de 2,2 μs en moyenne, et voyagent à une vitesse très proche de celle de la lumière. C'est-à-dire que durant leur vie entière ils ne parcourent que 660 m en moyenne.

Comment est-il possible de trouver des muons au sol (35 km plus bas) alors qu'ils ne peuvent parcourir que 660 m ?

Les muons ont une grande énergie, ainsi l'effet de dilatation temporelle décrite par la relativité restreinte les rend observables à la surface de la Terre.

En effet du point de vue de l'observateur au sol, la durée de vie du muon qui se déplace à la vitesse de la lumière est dilatée par un facteur γ (2,2 γ). De son point de vue le muon va vivre 75 fois plus longtemps et il sera possible de le trouver au sol. Du point de vue du muon, c'est la Terre qui se déplace vers lui à la vitesse de la lumière. Il verra la taille de la Terre réduite du même facteur γ. Pour le muon, les 35 km d'atmosphère ne feront plus que 660 m et il pourra atteindre le sol avant de disparaitre.

Les deux points de vue arrivent au même résultat physique. Du point de vue de l'observateur au sol il y a une dilatation du temps. Du point de vue du muon, il y a une contraction des longueurs. Tout comme avec la dilatation du temps, on n’observe pas la contraction des longueurs dans notre vie quotidienne, car nos vitesses de déplacement sont très faibles comparées à celle de la lumière.

Masse : De la Théorie à la Pratique

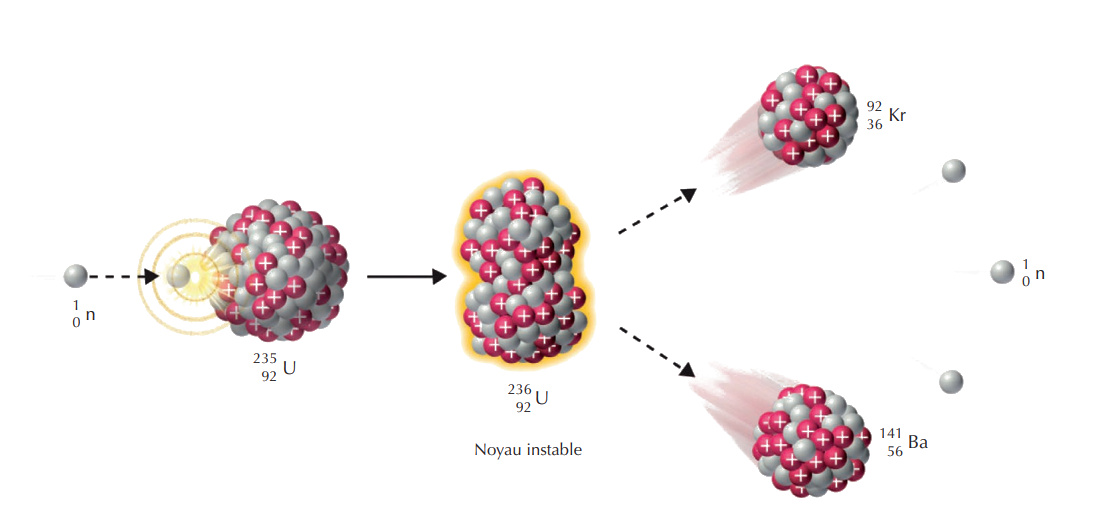
Dans E=mc2, l'énormité du facteur c2 nous dit qu'un objet possède une énergie gigantesque du seul fait qu'il a une masse.

Si on pouvait extraire toute l'énergie contenue dans 1 g de matière on obtiendrait 90000 GJ [E=0.001x(3x108)2=9x1016 joules] ou 25 GWh soit la production quotidienne d'une centrale nucléaire de 1 GW. L'énergie de masse contenu dans 1 mg de matière est égale à l'énergie chimique de 2 tonnes de pétrole (1 tonne de pétrole = 41,868 GJ). L'énergie de masse qui nous est cachée est vraiment gigantesque !!!
Un corps massif émet du rayonnement électromagnétique donc de la lumière (visible en particulier lorsqu'on chauffe un métal). Un corps massif perd de la masse dès lors qu'il perd de l'énergie. Autrement dit un corps peut perdre de la masse sans perdre de corpuscules. Ce qui veut dire que la masse ne mesure plus la quantité de matière d'un corps mais sa quantité d'énergie. Par exemple, la masse d'un noyau d'hydrogène n'est pas égale à la somme de la masse du proton plus celle de l'électron. Lorsque le proton et l'électron sont liés, le noyau tend vers un état fondamental parcimonieux (énergie potentielle la plus basse). Pour atteindre cet état fondamental, une quantité d'énergie ΔE est libérée ainsi l'énergie du système diminue. En perdant cette énergie extrêmement faible, le noyau perd aussi de la masse (ΔE=Δmc2). A l'inverse lorsque l'atome récupère de l'énergie le système augmente sa masse. Ceci est valable pour tous les atomes de la matière. Par exemple, la masse du noyau d'hélium (2 protons + 2 neutrons) = 6,646 yg (1 yoctogramme=10−24 gramme). La masse du proton = 1,673 yg. La masse du neutron = 1,675 yg. La masse des 2 protons + la masse des 2 neutrons = 6.696 yg. On constate que la masse du noyau est inférieure à la masse de ses constituants. Quand les protons et les neutrons se lient entre eux, la masse du système diminue de 1% Δm=ΔE/c2 (énergie potentielle la plus basse). Un ΔE est libéré. Ce n'est pas énorme mais cette énergie de fusion nucléaire permet aux étoiles de briller.
La masse d'un proton (2 quarks u + 1 quark d) est 1,673 yg soit 1,673x10-24 g. La masse d'un neutron (1 quark u + 2 quarks d) est 1,675 yg. La masse d'un quark u est 0,004 yg. La masse d'un quark d est 0,009 yg.

Pourquoi la masse des quarks ne représente qu'environ 2 millièmes de la masse des nucléons ? L'énergie cinétique et l'énergie d'interaction forte agitent et maintiennent les quarks ensemble. Ce qui veut dire que la masse ne contient que de l'énergie. La nature profonde de la masse c'est l'énergie due à la danse frénétique des particules élémentaires.

Si une particule qui émet de la lumière n'a pas de masse (m2c4=E2-p2c2) alors son énergie totale est égale à son énergie cinétique (E2-p2c2⇒E=pc). Ainsi, la masse est égale à l'inertie comme dans les équations de Newton (f=ma et f=mv).
Si une particule n'est pas au repos il faut ajouter l'impulsion (E2=m2c4+p2c2) ainsi la relativité restreinte rend possible l'existe
Si une particule a une vitesse égale à c son énergie est maximale, en conséquence, sa masse est nulle m2c4=E2-p2c2=0.
La masse est convertie en énergie (m=E/c2 ou Δm=ΔE/c2) dans la production de l'énergie nucléaire. Les noyaux atomiques très lourds (uranium 235, plutonium 239) contiennent énormément de protons, et sont instables. Si l'un de ces atomes capture un neutron, il se transforme en un noyau encore plus instable (236U ou 240Pu), et récupère de l'énergie. Le noyau résultant se divise en deux noyaux puis libère deux ou trois neutrons disponibles pour d'autres fissions de noyaux (principe de la réaction en chaine).

Dans cette réaction, la masse des deux noyaux plus la masse des neutrons libérés est plus faible que la masse du noyau d'uranium 235 initial. De la masse a été convertie en énergie cinétique. C'est cette énergie produite par la fission que l'on va récupérer. La fission d'un atome d'uranium 235 libère environ 193,2 MeV d'énergie récupérable. L'énergie libérée par les combustibles nucléaires est un million de fois plus grande que celle des énergies fossiles chimiques.

Les réactions chimiques transforment aussi de la masse en énergie mais à un niveau beaucoup plus faible de l'ordre de un milliardième.

Énergie : L'Évolution de la Notion d'Énergie

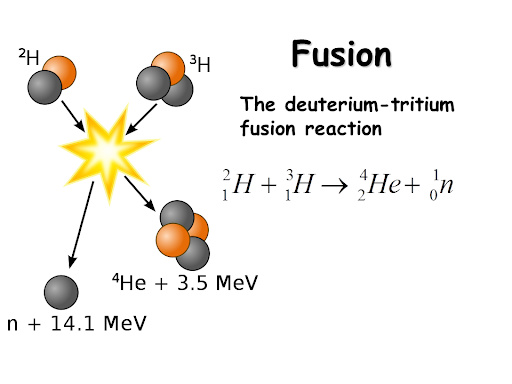
Le facteur de Lorentz (γ=1/√1-v2/c2) s'applique à tous les concepts dans un cadre relativiste et bien sûr l'énergie est concernée.

Dans l'équation E=mc2/√1-v2/c2-mc2, si la vitesse du corps est très petite par rapport à la vitesse de la lumière (jusqu'à 100 000 km/s) on retrouve l'énergie cinétique du monde macroscopique Ec=mc2/√1-v2/c2-mc2 ⇒ ½mv2
Si la vitesse s'approche de la vitesse de la lumière, l'énergie cinétique tend vers l'infini. Ce qui veut dire qu'on ne peut pas dépasser la vitesse de la lumière puisque pour communiquer à un objet une vitesse égale à c il faudrait une quantité d'énergie infinie Ec=∞ donc impossible. Autrement dit, plus un corps est massif et plus sa résistance au mouvement est grande. Plus sa vitesse augmente et plus il est difficile de modifier son mouvement. On atteint petit à petit une vitesse limite impossible à dépasser. A ce moment-là l'inertie est tellement élevée que toute l'énergie de l'univers ne suffirait pas à le faire aller plus vite. On comprend pourquoi la vitesse de la lumière est une vitesse limite dans tout l'Univers observable.
Ec=mc2/√1-v2/c2-mc2 dans cette équation, l'énergie cinétique est convertie en masse, c'est ce que l'on fait dans les accélérateurs de particules.

Les faisceaux de particules très énergétiques qui circulent en sens inverses et entrent en collision provoquent l'apparition d'un très grand nombre de particules que l'on repère grâce à des détecteurs de particules à haute énergie. Quand on mesure la masse totale de toutes les particules créées par la collision, et qu'on la compare à la masse des particules initiales, on trouve une valeur jusqu'à 200 000 fois plus élevée. En d'autres termes, la masse ne se conserve pas et l'énergie cinétique des particules initiales s'est matérialisée. Elle s'est transformée en nouvelles particules. L'énergie cinétique s'est transformée en masse !

Δm=ΔE/c2, dans la fusion thermonucléaire c'est la masse qui est convertie en énergie. Un noyau de deutérium ou un noyau de tritium chargés positivement ne peuvent pas se lier naturellement. Mais dans le tokamak sous l'influence d'une température et d'une pression extrêmes, les atomes d'hydrogène peuvent fusionner et générer de l'énergie. Le bilan des masses montre que la masse après la réaction de fusion est plus petite que la masse avant réaction. La différence de masse s'est transformée en énergie.

Antimatière : Une Réalité Cachée de notre Univers

L'antimatière est aussi une conséquence de l'équation E=mc2. La matière et l'antimatière en se rencontrant s'annihilent et transforment 100 % de leur masse en énergie pure.

Par exemple, un électron (négatif) et un positon (positif) peuvent fusionner et se transformer en photons gamma de très haute énergie. Ainsi, la conversion de la matière en énergie est totale.

Chaque fois qu'une particule rencontre une antiparticule elle s'annihile aussitôt en énergie pure comme dans la technique d’imagerie fonctionnelle de médecine nucléaire utilisée dans le TEP (tomographie par émission de positons). On injecte au patient un isotope radioactif (fluor 18) en microdose incorporée à une molécule dite "précurseur". Le produit va se diffuser dans les organes et de temps en temps le 18F-fluoro-deoxy-D-glucose (18FDG) se désintègre en émettant des positons. En présence des électrons de proximité, ces positons vont se désintégrer en émettant du rayonnement bêta. Ces photons vont traverser le corps du patient et être détecter par la machine. On pourra ainsi dire où est aller le glucose.

Les isotopes les plus couramment utilisés en imagerie TEP ont une période radioactive généralement courte (temps nécessaire à la décroissance de moitié de la radioactivité). Par conséquent, les radiotraceurs sont produits par un cyclotron quelques heures avant leur utilisation. La tomographies par émission de positons est une technique qui utilise l'antimatière.

N. B. : le rayonnement bêta est une forme de radioactivité dans laquelle un noyau émet un électron et un antineutrino (rayon bêta moins) ou un positron et un neutrino (rayon bêta plus). Ce processus donne naissance à un autre noyau ayant un neutron de moins et un proton de plus que le noyau initial.

Espace-Temps : Une Nouvelle Perspective sur l'Univers

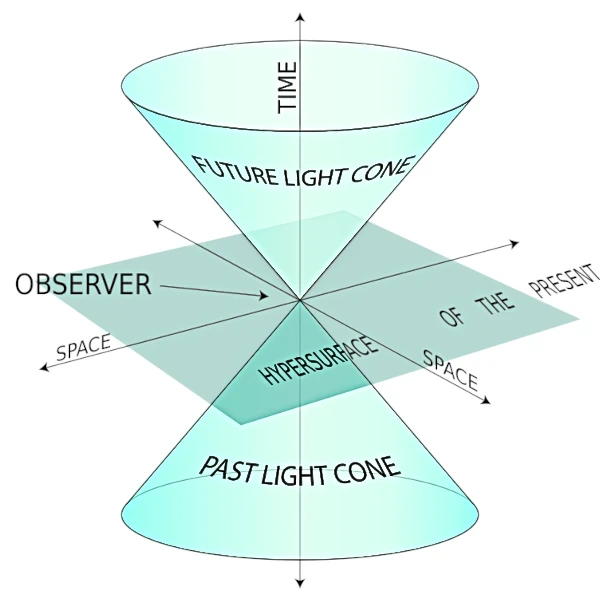
L'Espace-Temps est apparu avec la relativité restreinte et sa représentation géométrique a été reprise par Hermann Minkowski (1864-1909) en 1908.

Le continuum espace-temps comporte quatre dimensions. Trois dimensions pour l'espace (x, y, z) et une pour le temps (ct) que l'on transforme en distance en lui associant la constante c (d=ct). Dans l'espace-temps, le temps est géométrisé, ce qui permet à tous les évènements de se positionner dans le temps et l'espace par ses coordonnées ct, x, y, z qui dépendent toutes du référentiel car le temps ne se déroule pas de la même façon suivant le référentiel.

La mesure du temps transformée en mesure de distance peut être associée aux trois autres coordonnées de l'espace. Ainsi toutes les mesures sont en unités de distance. Le temps est devenu de l'espace !

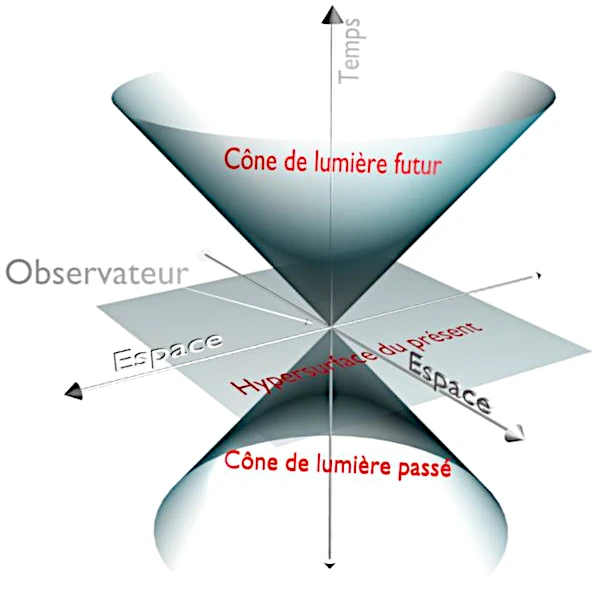
Tous les évènements ponctuels sont reliés à la vitesse de la lumière. L'ensemble de tous les évènements est appelé "l'espace-temps". La frontière définie par le cône de lumière est appelée "horizon cosmologique".

Les lignes d'univers définissant le cône peuvent être décrites par une particule se mouvant à la vitesse de la lumière ce qui définit la frontière du cône. La représentation des lignes d'Univers dans la partie inférieur (cône renversé) vient du fait qu'un évènement peut également avoir un passé. Si l'objet est immobile dans l'espace-temps, il ne se déplace pas dans l'espace mais se déplace dans le temps (axe vertical).

Si l'objet est en mouvement, nécessairement à une vitesse inférieure à c, le déplacement aura lieu à l'intérieur du cône de lumière ayant l'origine pour sommet (le présent). La ligne d'univers d'un personnage mobile a un angle dans le cône qui dépend de sa vitesse, il se déplace dans l'espace et dans le temps. Les bords du cône définissent la vitesse limite, celle des particules de lumière. La surface du cône est réservée à la représentation de la propagation des signaux lumineux émis par l'objet.

L'intérieur du cône de lumière du haut (côté positif) représente "l'avenir". Le sommet du cône de lumière représente le "ici et maintenant". L'intérieur du cône de lumière du bas (côté négatif) représente "le passé". L'extérieur du cône n'est pas accessible par un signal lumineux car il irait plus vite que la vitesse de la lumière. L'extérieur représente "le ailleurs".

Un corps du monde réel a une ligne d'univers dans l'espace-temps. L'ensemble de son histoire (tous les évènements de sa vie) trace cette ligne. Dans l'Univers euclidien à quatre dimensions de Minkowski, les trajectoires des objets dans l'espace-temps sont toujours des droites.

Ce qu'il faut retenir

La compréhension de la relativité restreinte est loin d'être immédiate, il faut beaucoup d'imagination pour comprendre les concepts qui se cachent derrière l'équation E=mc2. De très nombreux physiciens ont participé à l'émergence de cette formule dans l'esprit d'Einstein.

Galilée (1564-1642) pour la relativité galiléenne et le système de référence en mouvement uniforme.
Isaac Newton (1642-1727) pour ses lois du mouvement.
Michael Faraday (1791-1867) pour ses travaux sur l'électricité et le magnétisme.
James Clerk Maxwell (1831-1879) pour avoir unifié électricité et magnétisme et intégré la lumière dans le phénomène électromagnétique.
George Fitzgerald (1851-1901) pour la contraction des longueurs.
Hendrik Antoon Lorentz (1853-1928) pour la contraction des longueurs et la dilatation du temps.
Henri Poincaré (1854-1912) pour la structure de groupe des transformations de Lorentz.
Albert Abraham Michelson (1852-1931) et Edward Williams Morley (1838-1923) pour l'expérience sur l'invariance de la vitesse de la lumière dans l'éther luminifère.

Pour Einstein, la lumière est constituée de photons, il n'y a pas besoin d'éther luminifère.
Il existe une vitesse limite que les objets ne peuvent pas dépasser. Cette vitesse relie la masse et l'énergie.
c n'est plus la vitesse d'un objet sans masse mais devient une constante universelle de la physique que l'on va retrouver dans tous les phénomènes.
A la vitesse de la lumière le temps ne s'écoule plus. Il n'y a pas de vitesse 0, il n'y a pas de référentiel absolu. L'idée d'immobilité n'existe pas.
La simple application du facteur de Lorentz explique l'invariance de la vitesse de la lumière et sa limite, la dilatation du temps et la contraction des longueurs.
L'énergie et la matière sont de même nature. Pour que de l'énergie devienne de la masse il faut beaucoup d'énergie, pour que la masse devienne de l'énergie il faut très peu de masse. La masse d'un corps représente le contenant en énergie.
La matière et l'antimatière en se rencontrant s'annihilent et transforment 100 % de leur masse en énergie pure.
Le continuum espace-temps comporte quatre dimensions. Trois dimensions pour l'espace (x, y, z) et une pour le temps (ct) que l'on transforme en distance en lui associant la constante c (d=ct). Dans l'espace-temps, le temps est géométrisé.
Avec cette mystérieuse formule E=mc2 qui défie le sens commun, Albert Einstein a mis en équation tout l'univers, de l'infiniment grand à l'infiniment petit. E=mc2 réunit la cosmologie et la physique quantique. Si cette équation était mise en défaut c'est toute notre physique qui s'effondrerait.