Effet Tunnel : Explorer l’Invisible Atome par Atome

Effet tunnel : Un phénomène contre-intuitif mais réel

En mécanique classique, une particule confrontée à une barrière de potentiel plus élevée que son énergie est inévitablement réfléchie. Pourtant, dans le monde quantique, les lois sont différentes : une particule a une probabilité non nulle de traverser une telle barrière. C’est le célèbre effet tunnel. Ce phénomène découle directement de la nature ondulatoire des particules décrite par l’équation de Schrödinger.

Mathématiquement, la fonction d’onde $\psi(x)$ d’une particule dans une région interdite classiquement (où $E › V(x)$) ne s’annule pas, mais décroît exponentiellement : $$ \psi(x) \sim e^{-\kappa x}, \quad \text{avec } \kappa = \sqrt{\\frac{2m(V_0 - E)}{\hbar^2}}. $$ Ainsi, même si la densité de probabilité est très faible, elle n’est pas nulle, ce qui permet à la particule de « percer » la barrière.

Applications concrètes de l'effet tunnel

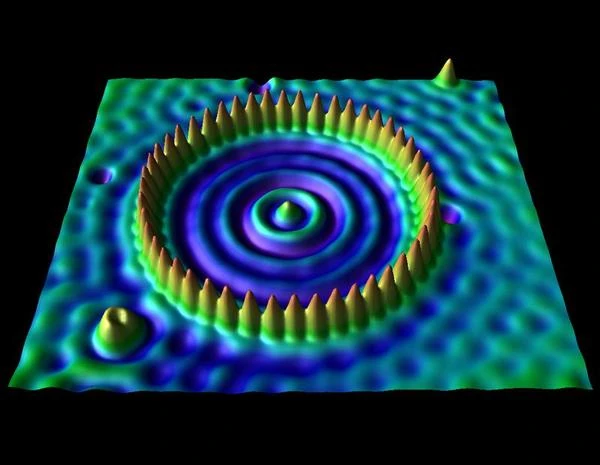
L’effet tunnel n’est pas un simple concept théorique : il a des applications technologiques majeures. L’exemple le plus emblématique est la microscopie à effet tunnel (STM), qui permet d’observer les surfaces avec une résolution atomique. Dans ce dispositif, un courant tunnel est mesuré entre une pointe conductrice et la surface d’un échantillon, séparés de quelques angströms seulement.

Autre exemple : le transistor à effet tunnel et les jonctions Josephson dans les circuits supraconducteurs, où l’effet tunnel permet le passage de paires de Cooper à travers une barrière isolante, phénomène crucial pour le développement des ordinateurs quantiques.

Même au niveau nucléaire, cet effet explique la décroissance alpha, où une particule alpha s’échappe du noyau atomique en franchissant une barrière de potentiel nucléaire.

Effet tunnel : Une fenêtre sur la nature probabiliste du monde quantique

L’effet tunnel remet en question notre intuition fondée sur la causalité classique. Il révèle que, dans le monde quantique, il n’existe pas de trajectoire déterministe. La mécanique quantique ne fournit que des probabilités. L'existence même de ce phénomène est une preuve expérimentale que les particules ne sont pas des objets localisés, mais des entités régies par des amplitudes de probabilité.

En somme, l’effet tunnel est l’un des joyaux les plus surprenants de la physique moderne. Il illustre parfaitement comment les règles de la mécanique quantique défient notre compréhension intuitive du monde, tout en ayant des répercussions concrètes dans les technologies avancées.

Le microscope à effet tunnel (STM)

Le Microscope à Effet Tunnel : Une Fenêtre sur le Monde Quantique

Le microscope à effet tunnel, inventé en 1981 par Gerd Binnig (1947-) et Heinrich Rohrer (1933-2013), prix Nobel 1986, repose directement sur le phénomène de l’effet tunnel quantique. Dans un STM, une pointe métallique très fine est approchée à une distance de l’ordre du nanomètre d’une surface conductrice. Lorsqu’une tension est appliquée entre la pointe et l’échantillon, un courant tunnel apparaît, bien que les deux ne soient pas en contact physique. Ce courant est extrêmement sensible à la distance entre la pointe et la surface (exponentiellement décroissant), ce qui permet de cartographier la topographie électronique avec une résolution latérale inférieure à 0,1 nm.

Le fonctionnement repose sur la densité d’états électroniques locaux (LDOS) de l’échantillon, accessible par le courant tunnel mesuré. En maintenant un courant constant via un système de rétroaction, la position verticale de la pointe révèle la topographie atomique de la surface. Ainsi, le STM permet de « voir » des atomes individuellement, ce qui en fait un outil fondamental en physique de la matière condensée, en nanotechnologie et en chimie de surface.