Espace-temps : L’Espace et le Temps Réunis

Fusion des dimensions d'espace et de temps

Avant le XXe siècle, l’espace et le temps étaient considérés comme des entités distinctes : l’espace était absolu, structurant les distances, tandis que le temps s’écoulait de manière uniforme. Autrement dit, l’espace était une scène rigide où tout se déployait, et le temps, un métronome infaillible qui battait la mesure sans jamais ralentir ni accélérer.

Cette vision newtonienne fut bouleversée en 1905 par la théorie de la relativité restreinte d’Albert Einstein (1879-1955), qui démontra que les mesures d’espace et de temps dépendent du référentiel de l’observateur, c'est-à-dire, de la position et au mouvement de celui qui regarde. Désormais, les événements doivent être décrits dans un cadre unifié à quatre dimensions : trois d’espace et une de temps.

Attention : Il est probablement impossible de concevoir l’espace-temps ?

Notre cerveau a été sélectionné pour naviguer dans un monde à trois dimensions spatiales et un temps linéaire. Or, la relativité nous impose d’imaginer quatre dimensions entremêlées, où l’espace et le temps ne sont plus indépendants, c'est cela qui est impossible.

Nous ne pouvons pas "voir" la quatrième dimension directement, seulement en analogies limitées en 3D et aucune image seule n’est suffisante.

• Le Miel Cosmique : "L'espace-temps est comme un miel épais. Plus on va vite, plus il résiste (c'est l'inertie). Près d'une masse, le miel devient plus visqueux - le temps s'écoule moins vite. Les objets y tracent des sillons en se déplaçant.".
• La pâte feuilletée : "L’espace et le temps sont feuilletés ensemble dans une seule pâte. En étirant la pâte dans un sens (agrandissement spatial), on l’amincit dans l’autre (réduction temporelle), et inversement.
• Le cube d’ombre : "Son ombre sur le mur est en 2D. Selon l’angle de projection, la forme de l’ombre change. L’espace-temps 4D que nous "projetons" dans notre perception 3D fonctionne un peu pareil : nous ne voyons qu’une projection, pas la structure complète.
• Le train en mouvement : "Dans un train en mouvement à vitesse constante, si vous lancez une balle vers le haut, elle retombe dans votre main. Pour quelqu'un à l'extérieur du train, la balle suit une trajectoire parabolique. Cela illustre comment le mouvement et le temps peuvent être perçus différemment selon le référentiel de l'observateur.
• Le film : "Dans un film, chaque image représente un instant dans le temps. L'espace-temps peut être vu comme un "film" de l'univers, où chaque "image" est une tranche de l'univers à un moment donné. L'ensemble du film représente l'espace-temps.
• Le tissu élastique : "Si vous placez une boule de bowling au centre, elle va s'enfoncer dans le tissu, créant une courbure. Si vous lancez ensuite une bille sur ce tissu, elle va tourner autour de la boule de bowling. Cette analogie montre comment les objets massifs courbent l'espace-temps et influencent le mouvement des autres objets.

L’espace, c’est du temps ; le temps, c’est de l’espace

Aucune analogie ne capture parfaitement les 4 dimensions + la courbure. Cependant, nous pouvons projeter des modèles mathématiques.

Des dimensions intimement liées

Dans la relativité restreinte, la relation entre l’espace et le temps est exprimée par l’invariance de l’intervalle d’espace-temps \(s^2\). \(s^2\) mesure la "distance" (séparation spatiale et temporelle) entre deux événements A et B dans l’espace-temps. Même si différents observateurs peuvent ne pas être d’accord sur la durée ou la distance qui les séparent, la combinaison des deux, donnée par \(s^2\), reste la même pour tous. C’est la règle de mesure universelle de l’espace-temps.

Expression de l'intervalle d'espace-temps en relativité restreinte

Cette expression est utilisée pour déterminer la nature de la séparation entre deux événements dans l'espace-temps. \[ \Delta s^2 = c^2\Delta t^2 - \Delta x^2 - \Delta y^2 - \Delta z^2 \] Cela signifie qu’un accroissement de la composante spatiale entraîne une diminution de la composante temporelle, et inversement.

Intervalle de type temps si \(\Delta s^2 > 0\)

Cela se produit lorsque la différence temporelle entre les deux événements est suffisamment grande pour que \(c^2\Delta t^2\) soit supérieur à la somme des carrés des différences spatiales \(\Delta x^2 + \Delta y^2 + \Delta z^2\).

Dans ce cas, les deux événements peuvent être reliés par un signal voyageant à une vitesse inférieure ou égale à la vitesse de la lumière. Cela signifie qu'un événement peut influencer l'autre de manière causale.

Les événements sont dits "séparés de manière temporelle", et il existe un référentiel dans lequel les deux événements se produisent au même endroit spatial, mais à des moments différents.

Intervalle de type espace si \(\Delta s^2 < 0\)

Cela se produit lorsque la somme des carrés des différences spatiales \(\Delta x^2 + \Delta y^2 + \Delta z^2\) est supérieure à \(c^2\Delta t^2\).

Dans ce cas, aucun signal ne peut voyager assez vite pour relier les deux événements sans dépasser la vitesse de la lumière. Les événements ne peuvent pas s'influencer causalement.

Les événements sont dits "séparés de manière spatiale", et il existe un référentiel dans lequel les deux événements se produisent au même moment temporel, mais à des endroits spatiaux différents.

En résumé

\(\Delta s^2 > 0\) indique une séparation temporelle où une influence causale est possible, tandis que \(\Delta s^2 < 0\) indique une séparation spatiale où aucune influence causale n'est possible.

Le cône de lumière et l’inclinaison du présent

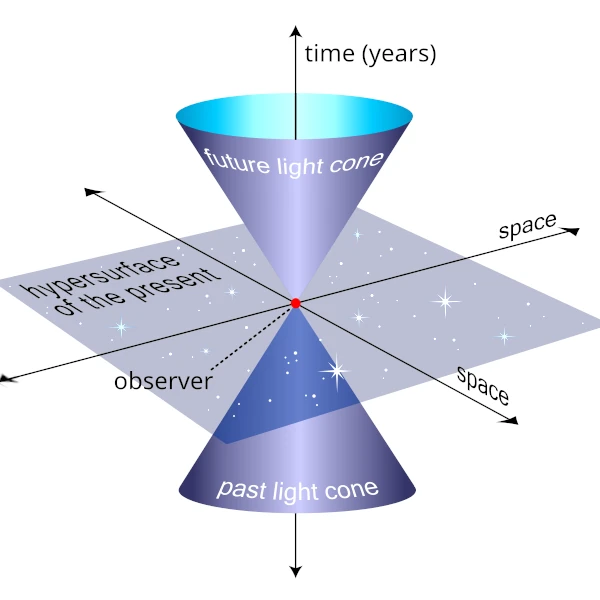
Le cône de lumière est la représentation graphique de toutes les trajectoires possibles que peut prendre la lumière depuis un événement donné. C'est la limite ultime de ce qui peut nous influencer et de ce que nous pouvons influencer.

• Le sommet des cônes : Ce point représente l'événement (position et temps) de l'observateur.
• Le cône du futur (le cône supérieur) : Il représente tous les endroits et tous les moments que la lumière, partant de votre position actuelle, pourrait atteindre. C'est l'ensemble des événements que vous pouvez potentiellement influencer. Rien ne peut aller plus vite que la lumière, donc tout événement que vous causez doit se trouver à l'intérieur ou sur la surface de ce cône.
• Le cône du passé (le cône inférieur) : Il représente tous les endroits et tous les moments d'où la lumière aurait pu partir pour arriver à votre position actuelle. C'est l'ensemble des événements qui peuvent potentiellement vous influencer. Rien ne peut voyager plus vite que la lumière, donc vous ne pouvez être influencé que par des événements qui se trouvent à l'intérieur ou sur la surface de ce cône.
• La surface des cônes : Il représente les trajectoires de la lumière elle-même. Les rayons de lumière voyagent à la vitesse maximale de l'univers, la vitesse de la lumière (c). La lumière d'un événement au sommet se propage vers l'extérieur, formant un cercle qui grandit avec le temps, créant la forme du cône. La pente des côtés du cône est fixée par la vitesse de la lumière.
• L'intérieur des cônes : Il représente toutes les trajectoires possibles pour des objets qui voyagent à une vitesse inférieure à celle de la lumière. Tout ce qui a une masse (comme vous) ne peut pas atteindre la vitesse de la lumière, donc vous êtes toujours à l'intérieur de votre cône de lumière.
• L'extérieur des cônes : C'est la zone d'espace-temps que la lumière ne peut atteindre à partir de l'événement initial. Ces événements sont dits absolument séparés ; ils ne peuvent ni nous influencer, ni être influencés par nous. Ils sont trop éloignés dans l'espace ou le temps.
• L'hypersurface du présent : Elle correspond à l'ensemble de tous les points de l'espace-temps qui sont simultanés pour un observateur donné. Ils sont causalement déconnectés de l'observateur car un événement simultané impliquerait une vitesse de transmission instantanée, ce qui est impossible.

Des situations extrêmes : trous noirs et inflation

Dans les trous noirs ou dans l’univers en expansion, l'interchangeabilité entre l'espace et le temps devient extrême : à l’horizon d’un trou noir, le temps se "fige" pour l’observateur distant, tandis que la coordonnée radiale devient temporelle. Dans l’univers primordial, où l’expansion de l’espace est rapide, le temps cosmique s’écoule plus lentement à mesure que l’espace "grandit". C’est une véritable dynamique compensée : l’expansion spatiale absorbe du temps.

Un échange compensé entre deux dimensions conjuguées

Ainsi, dans la physique relativiste, l’espace n’est pas indépendant du temps : ce sont deux faces d’une même entité. Une variation dans l’un implique une réponse dans l’autre, un peu comme deux variables conjuguées d’un système à somme constante. On pourrait dire : "quand l’espace s’étend, le temps ralentit".

Des conséquences mesurables

Le concept d’espace-temps permet de prédire des phénomènes mesurables : déviation de la lumière par les étoiles (lensing), dilatation du temps (temps plus lent en gravité forte), ou encore l’existence des ondes gravitationnelles, détectées pour la première fois en 2015 par LIGO. Ces ondulations dans l’espace-temps confirment que celui-ci est dynamique, déformable, ondulant comme une membrane cosmique.

L’espace-temps : Une structure topologique complexe

À l’échelle quantique ou cosmologique, l’espace-temps pourrait présenter des structures encore plus exotiques : trous de ver, fluctuations quantiques, ou "mousse" d’espace-temps selon la gravité quantique. Ces recherches sont à la frontière de la physique théorique, entre relativité générale et mécanique quantique.

Sources : Einstein Papers Project, LIGO Caltech, Scientific American – Einstein & Spacetime.