Spacetime: Space and Time United

Merging of space and time dimensions

Before the 20th century, space and time were considered separate entities: space was absolute, structuring distances, while time flowed uniformly. In other words, space was a rigid stage where everything unfolded, and time, an infallible metronome that kept the beat without ever slowing down or speeding up.

This Newtonian view was overturned in 1905 by Albert Einstein's (1879-1955) theory of special relativity, which demonstrated that measurements of space and time depend on the observer's frame of reference, that is, the position and movement of the observer. Henceforth, events must be described in a unified four-dimensional framework: three of space and one of time.

Warning: It is probably impossible to conceive of spacetime?

Our brain has been selected to navigate a world with three spatial dimensions and linear time. However, relativity forces us to imagine four intertwined dimensions, where space and time are no longer independent, which is impossible.

We cannot "see" the fourth dimension directly, only in limited 3D analogies, and no single image is sufficient.

• Cosmic Honey: "Spacetime is like thick honey. The faster you go, the more it resists (that's inertia). Near a mass, the honey becomes more viscous - time flows slower. Objects trace furrows as they move through it."
• Puff Pastry: "Space and time are layered together in a single dough. By stretching the dough in one direction (spatial enlargement), it thins in the other (temporal reduction), and vice versa."
• The Shadow Cube: "Its shadow on the wall is in 2D. Depending on the projection angle, the shape of the shadow changes. The 4D spacetime that we 'project' into our 3D perception works somewhat similarly: we only see a projection, not the complete structure."
• The Moving Train: "In a train moving at a constant speed, if you throw a ball upwards, it falls back into your hand. For someone outside the train, the ball follows a parabolic trajectory. This illustrates how motion and time can be perceived differently depending on the observer's frame of reference."
• The Film: "In a film, each frame represents a moment in time. Spacetime can be seen as a 'film' of the universe, where each 'frame' is a slice of the universe at a given moment. The entire film represents spacetime."
• The Elastic Fabric: "If you place a bowling ball in the center, it will sink into the fabric, creating a curve. If you then roll a marble on this fabric, it will orbit around the bowling ball. This analogy shows how massive objects bend spacetime and influence the movement of other objects."

Space is time; time is space

No analogy perfectly captures the 4 dimensions + curvature. However, we can project mathematical models.

Closely Linked Dimensions

In special relativity, the relationship between space and time is expressed by the invariance of the spacetime interval \(s^2\). \(s^2\) measures the "distance" (spatial and temporal separation) between two events A and B in spacetime. Even if different observers may disagree on the duration or distance separating them, the combination of both, given by \(s^2\), remains the same for all. This is the universal measuring rule of spacetime.

Expression of the spacetime interval in special relativity

This expression is used to determine the nature of the separation between two events in spacetime. \[ \Delta s^2 = c^2\Delta t^2 - \Delta x^2 - \Delta y^2 - \Delta z^2 \] This means that an increase in the spatial component results in a decrease in the temporal component, and vice versa.

Timelike interval if \(\Delta s^2 > 0\)

This occurs when the time difference between the two events is large enough for \(c^2\Delta t^2\) to be greater than the sum of the squares of the spatial differences \(\Delta x^2 + \Delta y^2 + \Delta z^2\).

In this case, the two events can be connected by a signal traveling at a speed less than or equal to the speed of light. This means that one event can causally influence the other.

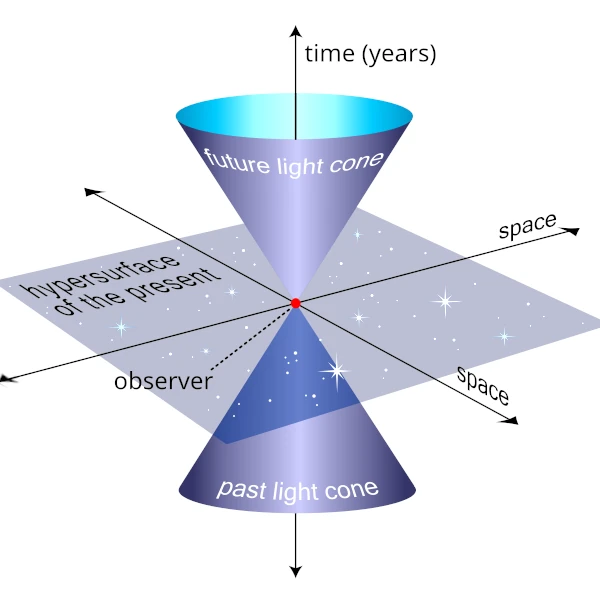
The events are said to be "timelike separated," and there exists a reference frame in which the two events occur at the same spatial location but at different times.

Spacelike interval if \(\Delta s^2 < 0\)

This occurs when the sum of the squares of the spatial differences \(\Delta x^2 + \Delta y^2 + \Delta z^2\) is greater than \(c^2\Delta t^2\).

In this case, no signal can travel fast enough to connect the two events without exceeding the speed of light. The events cannot causally influence each other.

The events are said to be "spacelike separated," and there exists a reference frame in which the two events occur at the same time but at different spatial locations.

In summary

\(\Delta s^2 > 0\) indicates a timelike separation where causal influence is possible, while \(\Delta s^2 < 0\) indicates a spacelike separation where no causal influence is possible.

The light cone and the tilt of the present

The light cone is the graphical representation of all possible paths that light can take from a given event. It is the ultimate limit of what can influence us and what we can influence.

• The apex of the cones: This point represents the observer's event (position and time).
• The future cone (the upper cone): It represents all the places and times that light, starting from your current position, could reach. It is the set of events that you can potentially influence. Nothing can travel faster than light, so any event you cause must be inside or on the surface of this cone.
• The past cone (the lower cone): It represents all the places and times from which light could have departed to arrive at your current position. It is the set of events that can potentially influence you. Nothing can travel faster than light, so you can only be influenced by events that are inside or on the surface of this cone.
• The surface of the cones: It represents the paths of light itself. Light rays travel at the maximum speed of the universe, the speed of light (c). The light from an event at the apex propagates outward, forming a circle that grows with time, creating the shape of the cone. The slope of the sides of the cone is set by the speed of light.
• The interior of the cones: It represents all possible paths for objects traveling at speeds less than that of light. Anything that has mass (like you) cannot reach the speed of light, so you are always inside your light cone.
• The exterior of the cones: This is the region of spacetime that light cannot reach from the initial event. These events are said to be absolutely separated; they can neither influence us nor be influenced by us. They are too far away in space or time.
• The hypersurface of the present: It corresponds to the set of all points in spacetime that are simultaneous for a given observer. They are causally disconnected from the observer because a simultaneous event would imply instantaneous transmission speed, which is impossible.

Extreme situations: black holes and inflation

In black holes or in the expanding universe, the interchangeability between space and time becomes extreme: at the horizon of a black hole, time "freezes" for the distant observer, while the radial coordinate becomes temporal. In the primordial universe, where the expansion of space is rapid, cosmic time flows more slowly as space "grows." It is a true compensated dynamic: spatial expansion absorbs time.

A compensated exchange between two conjugate dimensions

Thus, in relativistic physics, space is not independent of time: they are two faces of the same entity. A variation in one implies a response in the other, somewhat like two conjugate variables of a constant-sum system. One might say: "when space extends, time slows down."

Measurable consequences

The concept of spacetime allows us to predict measurable phenomena: the deflection of light by stars (lensing), time dilation (slower time in strong gravity), or the existence of gravitational waves, first detected in 2015 by LIGO. These ripples in spacetime confirm that it is dynamic, deformable, undulating like a cosmic membrane.

Spacetime: A complex topological structure

At the quantum or cosmological scale, spacetime could exhibit even more exotic structures: wormholes, quantum fluctuations, or "foam" of spacetime according to quantum gravity. These investigations are at the frontier of theoretical physics, between general relativity and quantum mechanics.

Sources: Einstein Papers Project, LIGO Caltech, Scientific American – Einstein & Spacetime.