Espaço-tempo: O Espaço e o Tempo Unidos

Fusão das dimensões de espaço e tempo

Antes do século XX, o espaço e o tempo eram considerados entidades distintas: o espaço era absoluto, estruturando as distâncias, enquanto o tempo fluía de maneira uniforme. Em outras palavras, o espaço era um palco rígido onde tudo se desenrolava, e o tempo, um metrônomo infalível que mantinha o ritmo sem nunca desacelerar nem acelerar.

Essa visão newtoniana foi revolucionada em 1905 pela teoria da relatividade restrita de Albert Einstein (1879-1955), que demonstrou que as medidas de espaço e tempo dependem do referencial do observador, ou seja, da posição e do movimento de quem observa. A partir de então, os eventos devem ser descritos em um quadro unificado de quatro dimensões: três de espaço e uma de tempo.

Atenção: É provavelmente impossível conceber o espaço-tempo?

Nosso cérebro foi selecionado para navegar em um mundo com três dimensões espaciais e um tempo linear. No entanto, a relatividade nos obriga a imaginar quatro dimensões entrelaçadas, onde o espaço e o tempo não são mais independentes, e é isso que é impossível.

Não podemos "ver" a quarta dimensão diretamente, apenas em analogias limitadas em 3D, e nenhuma imagem sozinha é suficiente.

• O Mel Cósmico: "O espaço-tempo é como um mel espesso. Quanto mais rápido você vai, mais ele resiste (isso é a inércia). Perto de uma massa, o mel fica mais viscoso - o tempo flui mais devagar. Os objetos traçam sulcos ao se moverem."
• A massa folhada: "O espaço e o tempo são folhados juntos em uma única massa. Ao esticar a massa em um sentido (aumento espacial), ela afinará no outro (redução temporal), e vice-versa."
• O cubo de sombra: "Sua sombra na parede está em 2D. Dependendo do ângulo de projeção, a forma da sombra muda. O espaço-tempo 4D que 'projetamos' em nossa percepção 3D funciona de maneira um pouco semelhante: só vemos uma projeção, não a estrutura completa."
• O trem em movimento: "Em um trem em movimento a uma velocidade constante, se você jogar uma bola para cima, ela cairá de volta em sua mão. Para alguém fora do trem, a bola segue uma trajetória parabólica. Isso ilustra como o movimento e o tempo podem ser percebidos de maneira diferente dependendo do referencial do observador."
• O filme: "Em um filme, cada quadro representa um instante no tempo. O espaço-tempo pode ser visto como um 'filme' do universo, onde cada 'quadro' é uma fatia do universo em um dado momento. O filme inteiro representa o espaço-tempo."
• O tecido elástico: "Se você colocar uma bola de boliche no centro, ela afundará no tecido, criando uma curvatura. Se você então lançar uma bolinha sobre esse tecido, ela orbitará em torno da bola de boliche. Essa analogia mostra como objetos massivos curvam o espaço-tempo e influenciam o movimento de outros objetos."

O espaço é tempo; o tempo é espaço

Nenhuma analogia captura perfeitamente as 4 dimensões + a curvatura. No entanto, podemos projetar modelos matemáticos.

Dimensões intimamente ligadas

Na relatividade restrita, a relação entre o espaço e o tempo é expressa pela invariância do intervalo de espaço-tempo \(s^2\). \(s^2\) mede a "distância" (separação espacial e temporal) entre dois eventos A e B no espaço-tempo. Mesmo que diferentes observadores possam não concordar sobre a duração ou a distância que os separa, a combinação de ambos, dada por \(s^2\), permanece a mesma para todos. Esta é a regra de medição universal do espaço-tempo.

Expressão do intervalo de espaço-tempo na relatividade restrita

Esta expressão é usada para determinar a natureza da separação entre dois eventos no espaço-tempo. \[ \Delta s^2 = c^2\Delta t^2 - \Delta x^2 - \Delta y^2 - \Delta z^2 \] Isso significa que um aumento no componente espacial resulta em uma diminuição no componente temporal, e vice-versa.

Intervalo do tipo tempo se \(\Delta s^2 > 0\)

Isso ocorre quando a diferença temporal entre os dois eventos é grande o suficiente para que \(c^2\Delta t^2\) seja maior que a soma dos quadrados das diferenças espaciais \(\Delta x^2 + \Delta y^2 + \Delta z^2\).

Neste caso, os dois eventos podem ser conectados por um sinal viajando a uma velocidade menor ou igual à velocidade da luz. Isso significa que um evento pode influenciar causalmente o outro.

Os eventos são ditos "separados de maneira temporal", e existe um referencial no qual os dois eventos ocorrem no mesmo local espacial, mas em momentos diferentes.

Intervalo do tipo espaço se \(\Delta s^2 < 0\)

Isso ocorre quando a soma dos quadrados das diferenças espaciais \(\Delta x^2 + \Delta y^2 + \Delta z^2\) é maior que \(c^2\Delta t^2\).

Neste caso, nenhum sinal pode viajar rápido o suficiente para conectar os dois eventos sem exceder a velocidade da luz. Os eventos não podem se influenciar causalmente.

Os eventos são ditos "separados de maneira espacial", e existe um referencial no qual os dois eventos ocorrem no mesmo momento temporal, mas em locais espaciais diferentes.

Em resumo

\(\Delta s^2 > 0\) indica uma separação temporal onde uma influência causal é possível, enquanto \(\Delta s^2 < 0\) indica uma separação espacial onde nenhuma influência causal é possível.

O cone de luz e a inclinação do presente

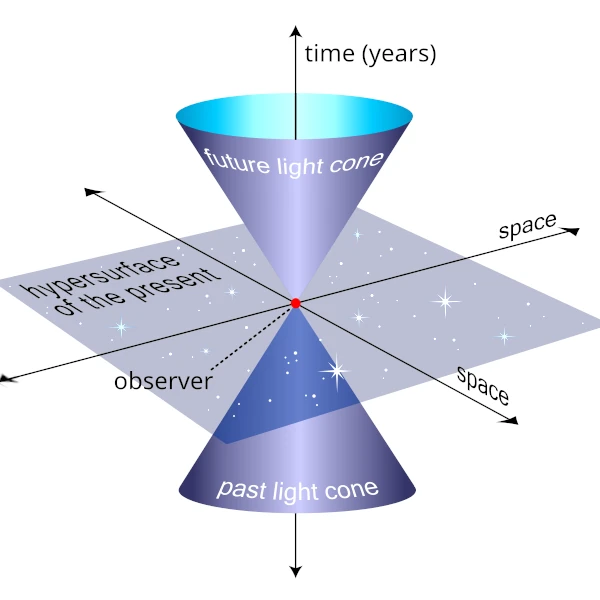
O cone de luz é a representação gráfica de todas as trajetórias possíveis que a luz pode tomar a partir de um evento dado. É o limite último do que pode nos influenciar e do que podemos influenciar.

• O vértice dos cones: Este ponto representa o evento do observador (posição e tempo).
• O cone do futuro (o cone superior): Representa todos os lugares e momentos que a luz, partindo da sua posição atual, poderia alcançar. É o conjunto de eventos que você pode potencialmente influenciar. Nada pode viajar mais rápido que a luz, então qualquer evento que você cause deve estar dentro ou na superfície deste cone.
• O cone do passado (o cone inferior): Representa todos os lugares e momentos de onde a luz poderia ter partido para chegar à sua posição atual. É o conjunto de eventos que podem potencialmente influenciar você. Nada pode viajar mais rápido que a luz, então você só pode ser influenciado por eventos que estão dentro ou na superfície deste cone.
• A superfície dos cones: Representa as trajetórias da luz em si. Os raios de luz viajam na velocidade máxima do universo, a velocidade da luz (c). A luz de um evento no vértice se propaga para fora, formando um círculo que cresce com o tempo, criando a forma do cone. A inclinação dos lados do cone é fixada pela velocidade da luz.
• O interior dos cones: Representa todas as trajetórias possíveis para objetos que viajam a uma velocidade inferior à da luz. Tudo o que tem massa (como você) não pode atingir a velocidade da luz, então você está sempre dentro do seu cone de luz.
• O exterior dos cones: Esta é a região do espaço-tempo que a luz não pode alcançar a partir do evento inicial. Esses eventos são ditos absolutamente separados; eles não podem nos influenciar, nem serem influenciados por nós. Eles estão muito distantes no espaço ou no tempo.
• A hipersuperfície do presente: Corresponde ao conjunto de todos os pontos no espaço-tempo que são simultâneos para um observador dado. Eles estão causalmente desconectados do observador, pois um evento simultâneo implicaria uma velocidade de transmissão instantânea, o que é impossível.

Situações extremas: buracos negros e inflação

Em buracos negros ou no universo em expansão, a intercambiabilidade entre espaço e tempo torna-se extrema: no horizonte de um buraco negro, o tempo "congela" para o observador distante, enquanto a coordenada radial torna-se temporal. No universo primordial, onde a expansão do espaço é rápida, o tempo cósmico flui mais lentamente à medida que o espaço "cresce". É uma verdadeira dinâmica compensada: a expansão espacial absorve o tempo.

Uma troca compensada entre duas dimensões conjugadas

Assim, na física relativística, o espaço não é independente do tempo: são duas faces de uma mesma entidade. Uma variação em um implica uma resposta no outro, um pouco como duas variáveis conjugadas de um sistema de soma constante. Poderíamos dizer: "quando o espaço se estende, o tempo desacelera".

Consequências mensuráveis

O conceito de espaço-tempo permite prever fenômenos mensuráveis: desvio da luz pelas estrelas (lente gravitacional), dilatação do tempo (tempo mais lento em gravidade forte), ou ainda a existência de ondas gravitacionais, detectadas pela primeira vez em 2015 pelo LIGO. Essas ondulações no espaço-tempo confirmam que este é dinâmico, deformável, ondulante como uma membrana cósmica.

Espaço-tempo: Uma estrutura topológica complexa

Na escala quântica ou cosmológica, o espaço-tempo poderia apresentar estruturas ainda mais exóticas: buracos de minhoca, flutuações quânticas, ou "espuma" de espaço-tempo segundo a gravidade quântica. Essas pesquisas estão na fronteira da física teórica, entre a relatividade geral e a mecânica quântica.

Fontes: Einstein Papers Project, LIGO Caltech, Scientific American – Einstein & Spacetime.