Espacio-tiempo: El Espacio y el Tiempo Unidos

Fusión de las dimensiones de espacio y tiempo

Antes del siglo XX, el espacio y el tiempo se consideraban entidades distintas: el espacio era absoluto, estructurando las distancias, mientras que el tiempo fluía de manera uniforme. En otras palabras, el espacio era un escenario rígido donde todo se desarrollaba, y el tiempo, un metronomo infalible que marcaba el ritmo sin ralentizarse ni acelerarse nunca.

Esta visión newtoniana fue trastornada en 1905 por la teoría de la relatividad especial de Albert Einstein (1879-1955), que demostró que las mediciones de espacio y tiempo dependen del marco de referencia del observador, es decir, de la posición y el movimiento de quien observa. A partir de entonces, los eventos deben describirse en un marco unificado de cuatro dimensiones: tres de espacio y una de tiempo.

Atención: ¿Es probablemente imposible concebir el espacio-tiempo?

Nuestro cerebro ha sido seleccionado para navegar en un mundo con tres dimensiones espaciales y un tiempo lineal. Sin embargo, la relatividad nos obliga a imaginar cuatro dimensiones entrelazadas, donde el espacio y el tiempo ya no son independientes, lo cual es imposible.

No podemos "ver" la cuarta dimensión directamente, solo en analogías limitadas en 3D, y ninguna imagen sola es suficiente.

• La Miel Cósmica: "El espacio-tiempo es como una miel espesa. Cuanto más rápido vas, más resiste (eso es la inercia). Cerca de una masa, la miel se vuelve más viscosa: el tiempo fluye más lento. Los objetos trazan surcos al moverse."
• La masa de hojaldre: "El espacio y el tiempo están hojaldrados juntos en una sola masa. Al estirar la masa en un sentido (agrandamiento espacial), se adelgaza en el otro (reducción temporal), y viceversa."
• El cubo de sombra: "Su sombra en la pared está en 2D. Según el ángulo de proyección, la forma de la sombra cambia. El espacio-tiempo 4D que 'proyectamos' en nuestra percepción 3D funciona de manera similar: solo vemos una proyección, no la estructura completa."
• El tren en movimiento: "En un tren en movimiento a velocidad constante, si lanzas una pelota hacia arriba, cae de nuevo en tu mano. Para alguien fuera del tren, la pelota sigue una trayectoria parabólica. Esto ilustra cómo el movimiento y el tiempo pueden ser percibidos de manera diferente según el marco de referencia del observador."
• La película: "En una película, cada fotograma representa un instante en el tiempo. El espacio-tiempo puede verse como una 'película' del universo, donde cada 'fotograma' es una porción del universo en un momento dado. Toda la película representa el espacio-tiempo."
• El tejido elástico: "Si colocas una bola de boliche en el centro, se hundirá en el tejido, creando una curvatura. Si luego lanzas una canica sobre este tejido, orbitará alrededor de la bola de boliche. Esta analogía muestra cómo los objetos masivos curvan el espacio-tiempo e influyen en el movimiento de otros objetos."

El espacio es tiempo; el tiempo es espacio

Ninguna analogía captura perfectamente las 4 dimensiones + la curvatura. Sin embargo, podemos proyectar modelos matemáticos.

Dimensiones íntimamente ligadas

En la relatividad especial, la relación entre el espacio y el tiempo se expresa mediante la invariancia del intervalo de espacio-tiempo \(s^2\). \(s^2\) mide la "distancia" (separación espacial y temporal) entre dos eventos A y B en el espacio-tiempo. Incluso si diferentes observadores pueden no estar de acuerdo sobre la duración o la distancia que los separa, la combinación de ambos, dada por \(s^2\), sigue siendo la misma para todos. Esta es la regla de medición universal del espacio-tiempo.

Expresión del intervalo de espacio-tiempo en la relatividad especial

Esta expresión se utiliza para determinar la naturaleza de la separación entre dos eventos en el espacio-tiempo. \[ \Delta s^2 = c^2\Delta t^2 - \Delta x^2 - \Delta y^2 - \Delta z^2 \] Esto significa que un aumento en el componente espacial resulta en una disminución en el componente temporal, y viceversa.

Intervalo de tipo tiempo si \(\Delta s^2 > 0\)

Esto ocurre cuando la diferencia de tiempo entre los dos eventos es lo suficientemente grande para que \(c^2\Delta t^2\) sea mayor que la suma de los cuadrados de las diferencias espaciales \(\Delta x^2 + \Delta y^2 + \Delta z^2\).

En este caso, los dos eventos pueden estar conectados por una señal que viaja a una velocidad menor o igual a la velocidad de la luz. Esto significa que un evento puede influir causalmente en el otro.

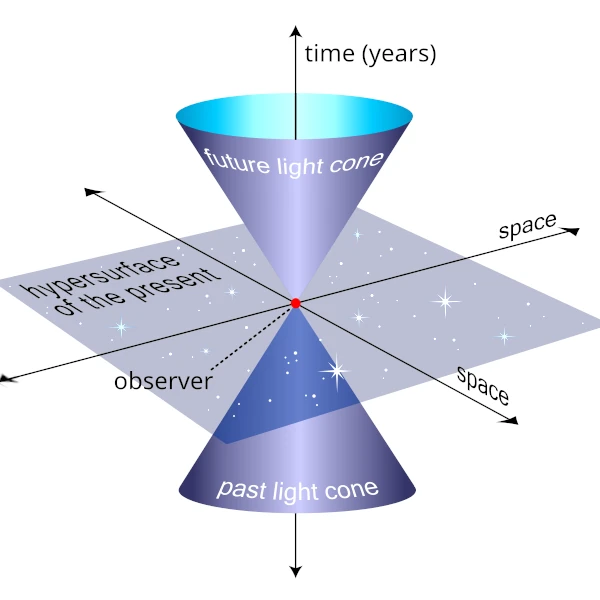
Los eventos se dice que están "separados de manera temporal", y existe un marco de referencia en el que los dos eventos ocurren en el mismo lugar espacial pero en diferentes momentos.

Intervalo de tipo espacio si \(\Delta s^2 < 0\)

Esto ocurre cuando la suma de los cuadrados de las diferencias espaciales \(\Delta x^2 + \Delta y^2 + \Delta z^2\) es mayor que \(c^2\Delta t^2\).

En este caso, ninguna señal puede viajar lo suficientemente rápido para conectar los dos eventos sin exceder la velocidad de la luz. Los eventos no pueden influirse causalmente entre sí.

Los eventos se dice que están "separados de manera espacial", y existe un marco de referencia en el que los dos eventos ocurren al mismo tiempo pero en diferentes lugares espaciales.

En resumen

\(\Delta s^2 > 0\) indica una separación de tipo tiempo donde la influencia causal es posible, mientras que \(\Delta s^2 < 0\) indica una separación de tipo espacio donde no es posible ninguna influencia causal.

El cono de luz y la inclinación del presente

El cono de luz es la representación gráfica de todas las trayectorias posibles que puede tomar la luz desde un evento dado. Es el límite último de lo que puede influirnos y de lo que podemos influir.

• El vértice de los conos: Este punto representa el evento del observador (posición y tiempo).
• El cono del futuro (el cono superior): Representa todos los lugares y momentos a los que la luz, partiendo de tu posición actual, podría llegar. Es el conjunto de eventos que potencialmente puedes influir. Nada puede viajar más rápido que la luz, por lo que cualquier evento que causes debe estar dentro o en la superficie de este cono.
• El cono del pasado (el cono inferior): Representa todos los lugares y momentos desde los cuales la luz podría haber partido para llegar a tu posición actual. Es el conjunto de eventos que potencialmente pueden influirte. Nada puede viajar más rápido que la luz, por lo que solo puedes ser influido por eventos que están dentro o en la superficie de este cono.
• La superficie de los conos: Representa las trayectorias de la luz misma. Los rayos de luz viajan a la velocidad máxima del universo, la velocidad de la luz (c). La luz de un evento en el vértice se propaga hacia afuera, formando un círculo que crece con el tiempo, creando la forma del cono. La pendiente de los lados del cono está fijada por la velocidad de la luz.
• El interior de los conos: Representa todas las trayectorias posibles para objetos que viajan a velocidades menores que la de la luz. Todo lo que tiene masa (como tú) no puede alcanzar la velocidad de la luz, por lo que siempre estás dentro de tu cono de luz.
• El exterior de los conos: Esta es la región del espacio-tiempo a la que la luz no puede llegar desde el evento inicial. Estos eventos se dice que están absolutamente separados; no pueden influirnos ni ser influenciados por nosotros. Están demasiado lejos en el espacio o en el tiempo.
• La hipersuperficie del presente: Corresponde al conjunto de todos los puntos en el espacio-tiempo que son simultáneos para un observador dado. Están causalmente desconectados del observador porque un evento simultáneo implicaría una velocidad de transmisión instantánea, lo cual es imposible.

Situaciones extremas: agujeros negros e inflación

En los agujeros negros o en el universo en expansión, la intercambiabilidad entre el espacio y el tiempo se vuelve extrema: en el horizonte de un agujero negro, el tiempo se "congela" para el observador distante, mientras que la coordenada radial se vuelve temporal. En el universo primordial, donde la expansión del espacio es rápida, el tiempo cósmico fluye más lentamente a medida que el espacio "crece". Es una verdadera dinámica compensada: la expansión espacial absorbe el tiempo.

Un intercambio compensado entre dos dimensiones conjugadas

Así, en la física relativista, el espacio no es independiente del tiempo: son dos caras de una misma entidad. Una variación en uno implica una respuesta en el otro, algo así como dos variables conjugadas de un sistema de suma constante. Podríamos decir: "cuando el espacio se extiende, el tiempo se ralentiza".

Consecuencias medibles

El concepto de espacio-tiempo nos permite predecir fenómenos medibles: la desviación de la luz por las estrellas (lente gravitacional), la dilatación del tiempo (tiempo más lento en gravedad fuerte), o la existencia de ondas gravitacionales, detectadas por primera vez en 2015 por LIGO. Estas ondulaciones en el espacio-tiempo confirman que este es dinámico, deformable, ondulante como una membrana cósmica.

Espacio-tiempo: Una estructura topológica compleja

A escala cuántica o cosmológica, el espacio-tiempo podría presentar estructuras aún más exóticas: agujeros de gusano, fluctuaciones cuánticas, o "espuma" de espacio-tiempo según la gravedad cuántica. Estas investigaciones están en la frontera de la física teórica, entre la relatividad general y la mecánica cuántica.

Fuentes: Einstein Papers Project, LIGO Caltech, Scientific American – Einstein & Spacetime.