Última actualización 26 de junio de 2015

Relatividad Restringida: El Comienzo de una Nueva Física

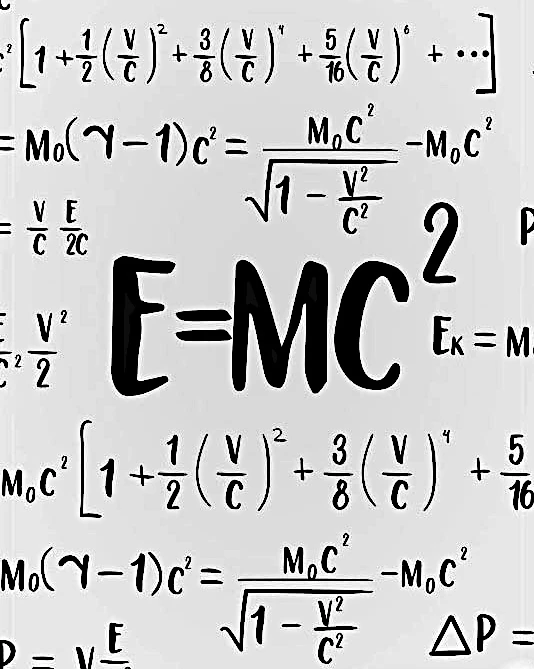
Ilustración del concepto de espacio-tiempo deformado

Un espacio-tiempo no absoluto

Antes de Einstein, el espacio y el tiempo se consideraban entidades absolutas, independientes del movimiento del observador. En 1905, Albert Einstein introdujo la relatividad restringida, revolucionando esta concepción newtoniana. Su teoría se basa en dos postulados fundamentales: las leyes de la física son las mismas en todos los marcos de referencia inerciales, y la velocidad de la luz en el vacío es constante e independiente de la velocidad de la fuente o del observador.

Estos dos supuestos tienen consecuencias sorprendentes: el tiempo no fluye de la misma manera para todos los observadores, las longitudes se contraen con la velocidad, y la simultaneidad se vuelve relativa. No es solo un cambio de marco, sino una revisión completa de nuestra percepción del universo.

Dilatación del tiempo y contracción de las longitudes

El fenómeno de la dilatación del tiempo predice que si un reloj se mueve a una velocidad cercana a la de la luz, será visto por un observador estacionario como funcionando más lentamente. Este enlentecimiento del tiempo está cuantificado por el factor de Lorentz:

$$ \gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}} $$

donde $ v $ es la velocidad del objeto y $ c $ es la velocidad de la luz. A un 90% de $ c $, $ \gamma \approx 2.3 $, lo que significa que el tiempo pasa más de dos veces más lentamente a bordo del objeto en movimiento.

A la inversa, para un observador en un marco de referencia en movimiento rápido, las longitudes en la dirección del movimiento se contraen. Esta es la contracción de las longitudes, otro efecto relativista, también medido por el factor de Lorentz.

Una elasticidad temporal insospechada

A primera vista, el tiempo parece universal y rígido: un segundo es un segundo, sin importar el observador. Sin embargo, la relatividad restringida muestra que esta rigidez es solo una ilusión a bajas velocidades. El factor de Lorentz aumenta lentamente a medida que la velocidad $ v $ aumenta, luego diverge rápidamente a medida que se acerca a $ c $. Para obtener un factor de dilatación del tiempo tan modesto como $ \gamma = 2.3 $, ya se debe alcanzar el 90% de la velocidad de la luz. Esto muestra que el tiempo es notablemente estable a velocidades ordinarias, pero se vuelve extremadamente maleable en regímenes relativistas.

Un lento aumento de los efectos relativistas

Este comportamiento se explica por la estructura geométrica del espacio-tiempo. A bajas velocidades ($ v \ll c $), el término $ v^2 / c^2 $ es muy pequeño, por lo que $ \gamma \approx 1 $, y los efectos relativistas son despreciables. Solo más allá de $ 0.8c $ la dilatación del tiempo se vuelve perceptible. Por ejemplo:

A $ v = 0.1c $, $ \gamma \approx 1.005 $
A $ v = 0.5c $, $ \gamma \approx 1.15 $
A $ v = 0.9c $, $ \gamma \approx 2.29 $
A $ v = 0.99c $, $ \gamma \approx 7.09 $
A $ v = 0.999999c $, $ \gamma \approx 707 $

El aumento es inicialmente lento, luego se vuelve explosivo a medida que se acerca a $ c $. Este comportamiento es una consecuencia directa de la naturaleza hiperbólica del cono de luz, que estructura el espacio-tiempo en la relatividad restringida.

El cono de luz y la deformación del tiempo

La nueva estructura del espacio-tiempo de Minkowski, utilizada en la relatividad restringida, tiene una métrica donde el intervalo invariante es: $ s^2 = c^2t^2 - x^2 - y^2 - z^2 $

Esta métrica separa los eventos en tres categorías: aquellos dentro del cono de luz (alcanzables causalmente), en el cono (límite de luz), y fuera del cono (no conectados causalmente). Cuando un observador se mueve a alta velocidad, su eje temporal se inclina en el diagrama de Minkowski, reduciendo la componente temporal visible para un observador en reposo. El tiempo se dilata: esta es una consecuencia geométrica, no un efecto "mecánico".

Simultaneidad relativa y causalidad

La relatividad restringida también introduce una noción contraintuitiva: dos eventos que parecen simultáneos en un marco pueden no serlo en otro. Esta relatividad de la simultaneidad resulta directamente de la invariancia de la velocidad de la luz.

A pesar de estos efectos, la relatividad restringida respeta la causalidad. Ninguna señal o partícula puede viajar más rápido que la luz, asegurando que las causas siempre precedan a sus efectos. Esto garantiza la consistencia lógica del mundo físico, incluso si ya no es absoluto.

La ecuación $ E = mc^2 $: una consecuencia geométrica

La famosa ecuación de Einstein $ E = mc^2 $ no es un postulado, sino una consecuencia directa de la geometría del espacio-tiempo en la relatividad restringida. Todo comienza con el invariante fundamental de la teoría: el intervalo de espacio-tiempo entre dos eventos, definido por: $ s^2 = c^2 t^2 - x^2 - y^2 - z^2 $

Este intervalo es constante para todos los observadores inerciales. Estructura el espacio-tiempo como una variedad pseudoeuclidiana, en el corazón de la formulación de Minkowski.

Del cuadrivector posición a la energía

Definimos el cuadrivector posición $ X^\mu = (ct, x, y, z) $, cuya derivada con respecto al tiempo propio $ \tau $ da el cuadrivector velocidad: $ U^\mu = \frac{dX^\mu}{d\tau} = \gamma (c, v_x, v_y, v_z) \quad \text{con} \quad \gamma = \frac{1}{\sqrt{1 - \frac{v^2}{c^2}}} $

Al multiplicar por la masa $ m $, obtenemos el cuadrivector energía-momento: $ P^\mu = m U^\mu = \left( \frac{E}{c}, \vec{p} \right) $

Este vector tiene una norma invariante relativista: $ P^\mu P_\mu = \left( \frac{E}{c} \right)^2 - p^2 = m^2 c^2 $

Lo que da la relación fundamental entre energía, momento y masa: $ E^2 = p^2 c^2 + m^2 c^4 $

Energía en reposo: la masa como energía condensada

Si el cuerpo está en reposo ($ \vec{p} = 0 $), obtenemos directamente: $ E = mc^2 $

Esta ecuación expresa la energía de masa en reposo, la energía intrínseca de cualquier cuerpo, incluso cuando está inmóvil. Revela que la masa es una forma concentrada de energía, lo que explica:

la liberación de energía en las reacciones nucleares,
la aniquilación materia-antimateria,
la estabilidad energética de las partículas elementales.

Así, $ E = mc^2 $ resulta naturalmente de la conservación del invariante de Minkowski y de la estructura del cuadrivector energía-momento. Es una manifestación profunda de la naturaleza geométrica de la física relativista.

La energía y la masa están vinculadas

La famosa ecuación $ E = mc^2 $ se deriva naturalmente de la relatividad restringida. Expresa la equivalencia entre masa y energía: una masa en reposo posee energía intrínseca proporcional al cuadrado de la velocidad de la luz. Esta relación tiene implicaciones mayores en la física nuclear y la cosmología.

Así, la relatividad restringida no es una curiosidad matemática: es la base de tecnologías modernas como el GPS, que debe tener en cuenta estos efectos para funcionar correctamente, y allana el camino para la relatividad general, que integra la gravitación en esta nueva geometría del espacio-tiempo.