E=mc²: Una Ecuación, Una Revolución

Relatividad Especial: Mucho Más Que Una Fórmula Famosa

E=mc² es la ecuación más conocida y popularizada de toda la física.

La ecuación E=mc² aparece por primera vez en el artículo de Albert Einstein titulado "¿Depende la inercia de un cuerpo de la energía que contiene?", publicado en la revista Annalen der Physik el 27 de septiembre de 1905. Aparece después del artículo del 30 de junio de 1905 titulado "Sobre la electrodinámica de los cuerpos en movimiento". Este artículo de junio de 1905 contiene la base de lo que luego se llamará "La Teoría de la Relatividad Especial".

La teoría de la relatividad especial se basa en dos principios: la relatividad galileana y la invariancia de la velocidad de la luz. La relatividad galileana dice que las leyes de la física permanecen invariables en los marcos de referencia inerciales (sistemas de referencia en movimiento uniforme), denominados desde entonces marcos galileanos. Además, la velocidad es relativa con respecto a un marco de referencia, un punto elegido arbitrariamente como fijo. La invariancia de la velocidad de la luz implica que es una velocidad límite e insuperable, independientemente del marco de referencia.

Pero, ¿qué significa exactamente la ecuación E=mc²?

En realidad, la ecuación original es E²=m²c⁴+p²c² (E=energía, m=masa, c=velocidad de la luz, p=impulso). En otras palabras, la energía total de un cuerpo es la suma de su energía de masa en reposo (m²c⁴) más su energía cinética (p²c²).

Si un cuerpo está inmóvil, su impulso es nulo, entonces E²=m²c⁴ ⇒ E=mc². Otras formas de la ecuación son m=E/c² o Δm=ΔE/c² (Δ=variación).

Esta ecuación E=mc² tiene enormes consecuencias en los conceptos de espacio, tiempo, masa y energía, así como en la física de lo infinitamente grande (cosmología) y de lo infinitamente pequeño (física cuántica).

N.B.: Ley de composición de velocidades: Si V1 es la velocidad del marco de referencia R1 (por ejemplo, un tren que viaja a 100 km/h) y V2 es la velocidad de un caminante (marco de referencia R2) que se mueve a 10 km/h en la misma dirección que el tren con respecto al tren, ¿a qué velocidad V0 se mueve el caminante con respecto a la plataforma (marco de referencia R0)? La respuesta es V0 = V1+V2=110 km/h. Desde el punto de vista de la plataforma, el tren se mueve a 100 km/h y el caminante a 110 km/h. Desde el punto de vista del tren, el caminante se mueve a 10 km/h y la plataforma a -100 km/h. Desde el punto de vista del caminante, el tren se mueve a -10 km/h y la plataforma a -110 km/h. La velocidad es relativa; depende del punto de vista. Ningún experimento mecánico dentro del marco de referencia inercial puede determinar la velocidad de su propio marco de referencia.

N.B.: El impulso o la cantidad de movimiento transmitida a un objeto es el producto de la masa por la velocidad (p=mv). Esto corresponde a la inercia del objeto o la dificultad para cambiar su movimiento.

Éter Luminífero: Cuando la Luz Viaja en el Éter

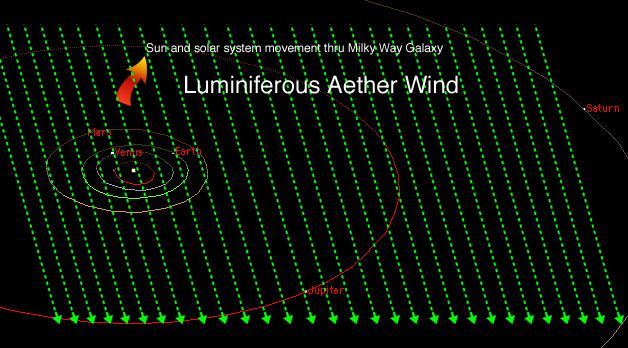
En el artículo del 30 de junio de 1905, publicado en Annalen der Physik "Sobre la electrodinámica de los cuerpos en movimiento", Einstein postula que la luz no es solo ondulatoria, sino que también consiste en fotones (corpúsculos de luz). Esto le permitirá cuestionar la existencia del éter.

La luz, redefinida por Maxwell, ha sido considerada desde el siglo XVII como una onda. El sonido necesita un medio (aire) que vibra al pasar el sonido. De manera similar, una onda necesita un medio (agua) para propagarse. Los físicos del siglo XVIII inventaron entonces el éter luminífero, un sustrato inmaterial que sirve como soporte en el vacío para transportar la luz. El éter que vibra al pasar la luz era un consenso en el mundo científico. Para Einstein, si la luz no es solo ondulatoria, sino que también consiste en fotones, entonces no hay necesidad de éter luminífero.

Einstein rechazó enérgicamente la naturaleza estacionaria del éter defendida por Lorentz porque era contraria al principio de relatividad. La luz puede propagarse en el vacío como corpúsculos.

N.B.: Según las ecuaciones de James Clerk Maxwell (1831-1879), la luz es una onda electromagnética transversal autopropagante con componentes eléctricas y magnéticas donde los campos eléctricos y magnéticos oscilan en ángulo recto entre sí y se propagan perpendicularmente a la dirección en la que se mueven indefinidamente a menos que sean absorbidos por la materia intermedia. En otras palabras, cada tipo de campo—eléctrico y magnético—genera el otro para propagar toda la estructura compuesta en el espacio vacío a la velocidad finita de la luz, c (del latín celeritas "velocidad").

Velocidad de la Luz: El Límite Definitivo de la Naturaleza

La eliminación del éter nos dice que la noción de velocidad absoluta no existe; la velocidad es relativa. Esto implica que si un objeto tiene una velocidad c en un marco de referencia, entonces tiene una velocidad c en todos los marcos de referencia.

¿Cómo aceptar esta rareza?

Los siguientes postulados son necesarios para entender la teoría de la relatividad especial.

• No hay un punto privilegiado en el espacio y el tiempo; el espacio-tiempo es homogéneo. Si se realiza un experimento, las mediciones seguirán siendo válidas aquí y allá, ayer y mañana.
• No hay una dirección privilegiada en el espacio (el espacio es isotrópico). Si se realiza un experimento, las mediciones seguirán siendo válidas en todas las direcciones del espacio, a diferencia del tiempo, que siempre va en la misma dirección (del pasado al futuro).
• Las mismas leyes de transformación relacionan las mediciones de los experimentos vistas por observadores situados en diferentes marcos de referencia inerciales.
• Si un evento A es la causa de un evento B, independientemente del observador, el evento A siempre será la causa del evento B. La causalidad debe ser respetada, lo que significa que el orden de los eventos nunca se invertirá independientemente del movimiento.

Si aceptamos estos postulados, las transformaciones de Lorentz (1853-1928) modifican la ley de composición de velocidades.

V=V1+V2 se convierte en V=(V1+V2)/(1 + V1V2/c²)

Se demuestra que si V2=c ⇒ V=c. La energía de V2 siendo máxima, la velocidad V1 es cero.

V=(V1+c)/(1+V1c/c²)=(V1+c)/(1+V1/c)=c(V1+c)/(c+V1)=c

c se ha convertido en una constante límite, y los objetos que se mueven a la velocidad c no dependen del marco de referencia. Si un objeto se propaga a la velocidad de la luz, entonces se propagará a la velocidad de la luz para todos los observadores. El experimento da c=299,792,458 m/s. A nuestra escala, V1 y V2 son pequeñas en comparación con c, por lo que el factor de Lorentz (γ=1/√(1-v²/c²)) muy cercano a 1 nos permite encontrar V≈V1+V2.

El factor de Lorentz es el factor de proporcionalidad por el cual el tiempo, las longitudes y la masa relativistas cambian para un objeto mientras está en movimiento. Este factor toma un valor infinito cuando la velocidad del objeto alcanza la velocidad de la luz.

γ=1/√(1-v²/c²) ⇒ γ=1/√(1-c²/c²) ⇒ γ=1/0 = ∞

La gráfica del factor de Lorentz muestra una asíntota. Esta asíntota se eleva bruscamente verticalmente a medida que v se acerca a c. Aquí hay algunos valores del factor de Lorentz correspondientes a diferentes valores de velocidad.

• Al 10% de c, el factor γ=1.005
• Al 20% de c, el factor γ=1.021
• Al 50% de c, el factor γ=1.16
• Al 99% de c, el factor γ≈7
• Al 99.9% de c, el factor γ≈22
• Al 99.99% de c, el factor γ≈71
• Al 100% de c, el factor gamma es infinito.

Dilatación del Tiempo: El Impacto de la Velocidad y la Gravedad

El factor de Lorentz (γ=1/√(1-v²/c²)) se aplica a todos los conceptos en un marco relativista, y por supuesto, el tiempo está concernido.

Un rayo láser que se refleja en la Luna tarda 1.3 segundos en ir y 1.3 segundos en volver. El movimiento de ida y vuelta del rayo láser que viaja entre 2 espejos puede considerarse un reloj. Un piloto que pasa a muy alta velocidad junto a la Tierra observa un fenómeno extraño. Ve la luz moviéndose en un viaje de ida y vuelta no verticalmente sino en zigzag. El rayo recorre una distancia más larga para él que para un observador en la Tierra. La dirección del láser vista por el observador en el suelo es vertical, por lo que la distancia es más corta que la vista por el piloto.

Dado que v=dt y la velocidad de la luz es invariante, si v es invariante y la distancia d es mayor, entonces el tiempo es más corto. Desde el punto de vista del piloto, el péndulo de luz oscila más lentamente que para el observador en la Tierra.

En la nave espacial, el tiempo se dilata por un factor γ, que es una función de la velocidad de la nave. El movimiento causa una desaceleración del tiempo. Esto se ha demostrado prácticamente con relojes atómicos que permiten mediciones extremadamente precisas. Dos relojes atómicos, uno instalado en un avión en vuelo y el otro colocado en el suelo, obtienen mediciones de tiempo diferentes. Hay una desincronización de los relojes. El reloj del avión es más lento por unos pocos nanosegundos, pero la diferencia es real y medible. Esta pequeña diferencia se debe a la baja velocidad del avión en comparación con la velocidad de la luz.

Contracción de Longitudes: Un Efecto Relativista Fundamental

El factor de Lorentz (γ=1/√(1-v²/c²)) se aplica a todos los conceptos en un marco relativista. Las longitudes también están concernidas.

Para medir la longitud de un objeto en movimiento, sus extremos deben medirse simultáneamente (en exactamente el mismo momento). Esto no es posible para un objeto que viaja a la velocidad de la luz. Para medirlo, debe estar estacionario. Por lo tanto, uno debe estar en su propio marco de referencia donde el objeto está estacionario.

En su marco de referencia, la longitud de los objetos en movimiento se reduce por un factor gamma. Para entender este fenómeno de contracción de longitudes, un ejemplo será más explícito que las ecuaciones.

Los muones son partículas elementales con una carga eléctrica negativa, inestables, producidas en la atmósfera superior a una altitud de 35 km. Los rayos cósmicos son flujos de núcleos atómicos (protones) de alta energía relativista, provenientes del espacio. Cuando los rayos cósmicos chocan con átomos de oxígeno o nitrógeno en la atmósfera superior, producen lluvias de partículas, incluyendo muones. Los muones tienen una vida útil de 2.2 μs en promedio y viajan a una velocidad muy cercana a la de la luz. Esto significa que durante toda su vida, solo recorren un promedio de 660 metros.

¿Cómo es posible encontrar muones en el suelo (35 km más abajo) cuando solo pueden viajar 660 m?

Los muones tienen mucha energía, por lo que el efecto de dilatación del tiempo descrito por la relatividad especial los hace observables en la superficie de la Tierra.

De hecho, desde el punto de vista del observador en el suelo, la vida útil del muón que se mueve a la velocidad de la luz se dilata por un factor γ (2.2 γ). Desde su punto de vista, el muón vivirá 75 veces más y será posible encontrarlo en el suelo. Desde el punto de vista del muón, es la Tierra la que se mueve hacia él a la velocidad de la luz. Verá el tamaño de la Tierra reducido por el mismo factor γ. Para el muón, los 35 km de la atmósfera serán solo 660 m, y podrá alcanzar el suelo antes de desaparecer.

Ambos puntos de vista llevan al mismo resultado físico. Desde el punto de vista del observador en el suelo, hay una dilatación del tiempo. Desde el punto de vista del muón, hay una contracción de longitudes. Al igual que con la dilatación del tiempo, no observamos la contracción de longitudes en nuestra vida diaria porque nuestras velocidades de desplazamiento son muy bajas en comparación con la velocidad de la luz.

Masa: De la Teoría a la Práctica

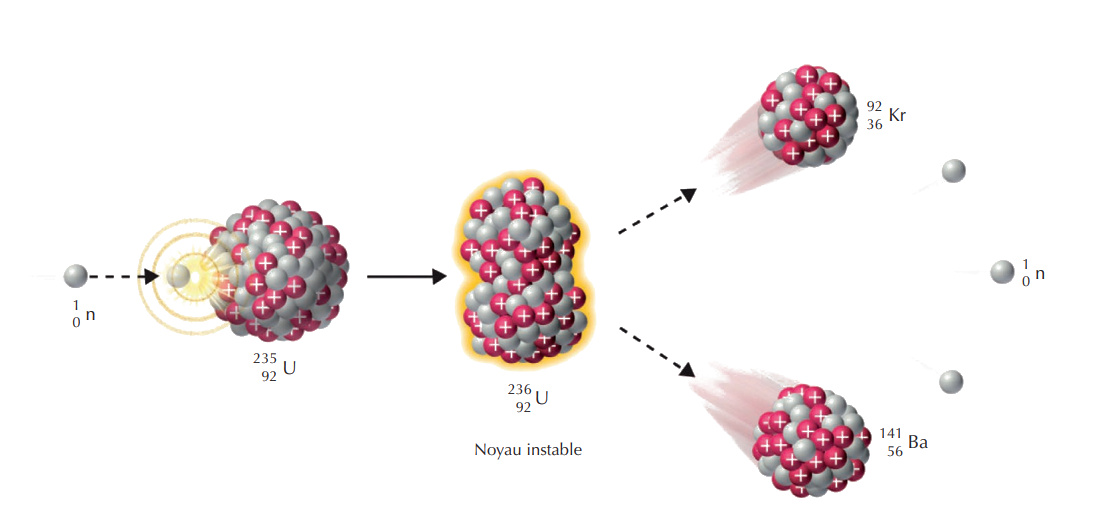
En E=mc², la enormidad del factor c² nos dice que un objeto posee una cantidad gigantesca de energía solo por virtud de su masa.

• Si pudiéramos extraer toda la energía contenida en 1 gramo de materia, obtendríamos 90,000 GJ [E=0.001x(3x10⁸)²=9x10¹³ julios] o 25 GWh, que es la producción diaria de una planta de energía nuclear de 1 GW. La energía de masa contenida en 1 mg de materia es igual a la energía química de 2 toneladas de petróleo (1 tonelada de petróleo = 41.868 GJ). ¡La energía de masa oculta para nosotros es verdaderamente gigantesca!
• Un cuerpo masivo emite radiación electromagnética, por lo tanto, luz (visible especialmente al calentar un metal). Un cuerpo masivo pierde masa tan pronto como pierde energía. En otras palabras, un cuerpo puede perder masa sin perder partículas. Esto significa que la masa ya no mide la cantidad de materia en un cuerpo, sino su cantidad de energía. Por ejemplo, la masa de un núcleo de hidrógeno no es igual a la suma de la masa del protón más la del electrón. Cuando el protón y el electrón están unidos, el núcleo tiende hacia un estado fundamental parsimonioso (energía potencial más baja). Para alcanzar este estado fundamental, se libera una cantidad de energía ΔE, por lo que la energía del sistema disminuye. Al perder esta cantidad extremadamente pequeña de energía, el núcleo también pierde masa (ΔE=Δmc²). Por el contrario, cuando el átomo recupera energía, el sistema aumenta su masa. Esto es válido para todos los átomos de la materia. Por ejemplo, la masa del núcleo de helio (2 protones + 2 neutrones) = 6.646 yg (1 yoctograma = 10⁻²⁴ gramos). La masa del protón = 1.673 yg. La masa del neutrón = 1.675 yg. La masa de los 2 protones + la masa de los 2 neutrones = 6.696 yg. Se observa que la masa del núcleo es menor que la masa de sus constituyentes. Cuando los protones y neutrones se unen, la masa del sistema disminuye en un 1% Δm=ΔE/c² (energía potencial más baja). Se libera un ΔE. Esto no es enorme, pero esta energía de fusión nuclear permite que las estrellas brillen.
• La masa de un protón (2 quarks arriba + 1 quark abajo) es 1.673 yg o 1.673x10⁻²⁴ g. La masa de un neutrón (1 quark arriba + 2 quarks abajo) es 1.675 yg. La masa de un quark arriba es 0.004 yg. La masa de un quark abajo es 0.009 yg.

¿Por qué la masa de los quarks representa solo alrededor de 2 milésimas de la masa de los nucleones?

La energía cinética y la energía de interacción fuerte agitan y mantienen unidos a los quarks. Esto significa que la masa contiene solo energía. La naturaleza profunda de la masa es la energía debido a la danza frenética de las partículas elementales.

• Si una partícula que emite luz no tiene masa (m²c⁴=E²-p²c²), entonces su energía total es igual a su energía cinética (E²-p²c² ⇒ E=pc). Así, la masa es igual a la inercia como en las ecuaciones de Newton (f=ma y f=mv).
• Si una partícula no está en reposo, se debe agregar el impulso (E²=m²c⁴+p²c²), por lo que la relatividad especial permite la existencia de partículas sin masa. Una partícula puede tener energía sin tener masa; es suficiente que su impulso no sea cero. Este es el caso de los fotones. Las partículas sin masa no pueden estar en reposo; están obligadas a viajar a la velocidad de la luz.
• Si una partícula tiene una velocidad igual a c, su energía es máxima; en consecuencia, su masa es cero m²c⁴=E²-p²c²=0.
• La masa se convierte en energía (m=E/c² o Δm=ΔE/c²) en la producción de energía nuclear. Los núcleos atómicos muy pesados (uranio-235, plutonio-239) contienen muchos protones y son inestables. Si uno de estos átomos captura un neutrón, se transforma en un núcleo aún más inestable (²³⁶U o ²⁴⁰Pu) y gana energía. El núcleo resultante se divide en dos núcleos y luego libera dos o tres neutrones disponibles para otras fisiones nucleares (principio de la reacción en cadena).

En esta reacción, la masa de los dos núcleos más la masa de los neutrones liberados es menor que la masa del núcleo inicial de uranio-235. La masa se ha convertido en energía cinética. Es esta energía producida por la fisión la que recuperaremos. La fisión de un átomo de uranio-235 libera aproximadamente 193.2 MeV de energía recuperable. La energía liberada por los combustibles nucleares es un millón de veces mayor que la de los combustibles fósiles químicos.

• Las reacciones químicas también convierten masa en energía, pero a un nivel mucho más bajo, del orden de una milmillonésima.

Energía: La Evolución del Concepto de Energía

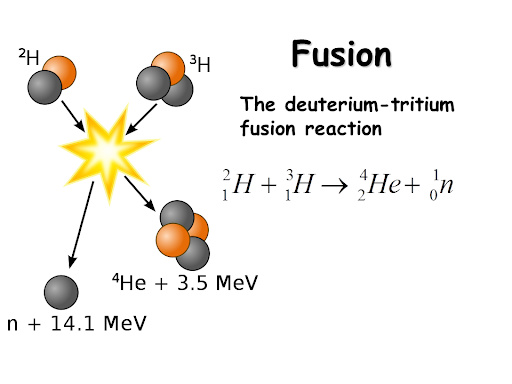
El factor de Lorentz (γ=1/√(1-v²/c²)) se aplica a todos los conceptos en un marco relativista, y por supuesto, la energía está concernida.

• En la ecuación E=mc²/√(1-v²/c²)-mc², si la velocidad del cuerpo es muy pequeña en comparación con la velocidad de la luz (hasta 100,000 km/s), encontramos la energía cinética del mundo macroscópico Ec=mc²/√(1-v²/c²)-mc² ⇒ ½mv².
• Si la velocidad se acerca a la velocidad de la luz, la energía cinética tiende hacia el infinito. Esto significa que no es posible exceder la velocidad de la luz porque para dar a un objeto una velocidad igual a c, se requeriría una cantidad infinita de energía, Ec=∞, lo cual es imposible. En otras palabras, cuanto más masivo es un cuerpo, mayor es su resistencia al movimiento. Cuanto más rápido se mueve, más difícil es cambiar su movimiento. Gradualmente alcanzamos una velocidad límite que no puede ser excedida. En ese punto, la inercia es tan alta que toda la energía del universo no sería suficiente para hacerlo ir más rápido. Entendemos por qué la velocidad de la luz es una velocidad límite en todo el universo observable.
• Ec=mc²/√(1-v²/c²)-mc² en esta ecuación, la energía cinética se convierte en masa, que es lo que hacemos en los aceleradores de partículas.

Los haces de partículas de alta energía que circulan en direcciones opuestas y chocan causan la aparición de un gran número de partículas que se detectan utilizando detectores de partículas de alta energía. Cuando medimos la masa total de todas las partículas creadas por la colisión y la comparamos con la masa de las partículas iniciales, encontramos un valor hasta 200,000 veces mayor. En otras palabras, la masa no se conserva, y la energía cinética de las partículas iniciales se ha materializado. Se ha transformado en nuevas partículas. ¡La energía cinética se ha transformado en masa!

• Δm=ΔE/c², en la fusión termonuclear, la masa se convierte en energía. Un núcleo de deuterio o un núcleo de tritio cargados positivamente no pueden unirse naturalmente. Pero en el tokamak, bajo la influencia de una temperatura y presión extremas, los átomos de hidrógeno pueden fusionarse y generar energía. El balance de masas muestra que la masa después de la reacción de fusión es menor que la masa antes de la reacción. La diferencia de masa se ha transformado en energía.

Antimateria: Una Realidad Oculta de Nuestro Universo

La antimateria también es una consecuencia de la ecuación E=mc². La materia y la antimateria, al encontrarse, se aniquilan y transforman el 100% de su masa en energía pura.

• Por ejemplo, un electrón (negativo) y un positrón (positivo) pueden fusionarse y transformarse en fotones gamma de muy alta energía. Así, la conversión de materia en energía es total.

Cada vez que una partícula se encuentra con una antipartícula, se aniquila instantáneamente en energía pura, como en la técnica de imagen funcional de medicina nuclear utilizada en la PET (tomografía por emisión de positrones). Se inyecta al paciente un isótopo radiactivo (flúor-18) en una microdosis incorporada a una molécula "precursora". El producto se difundirá en los órganos, y de vez en cuando, el ¹⁸F-fluoro-deoxi-D-glucosa (¹⁸FDG) se desintegrará, emitiendo positrones. En presencia de electrones cercanos, estos positrones se desintegrarán, emitiendo radiación beta. Estos fotones atravesarán el cuerpo del paciente y serán detectados por la máquina. Así podremos determinar dónde ha ido la glucosa.

Los isótopos más comúnmente utilizados en la imagen PET tienen una vida media radiactiva generalmente corta (tiempo requerido para que la mitad de la radiactividad decaiga). En consecuencia, los radiotrazadores son producidos por un ciclotrón unas horas antes de su uso. La tomografía por emisión de positrones es una técnica que utiliza la antimateria.

N.B.: La radiación beta es una forma de radiactividad en la que un núcleo emite un electrón y un antineutrino (radiación beta menos) o un positrón y un neutrino (radiación beta más). Este proceso da lugar a otro núcleo que tiene un neutrón menos y un protón más que el núcleo inicial.

Espacio-Tiempo: Una Nueva Perspectiva del Universo

El espacio-tiempo surgió con la relatividad especial, y su representación geométrica fue retomada por Hermann Minkowski (1864-1909) en 1908.

El continuo espacio-tiempo tiene cuatro dimensiones. Tres dimensiones para el espacio (x, y, z) y una para el tiempo (ct), que se transforma en una distancia asociándola con la constante c (d=ct). En el espacio-tiempo, el tiempo está geometrizado, lo que permite que todos los eventos se posicionen en el tiempo y el espacio por sus coordenadas ct, x, y, z, todas las cuales dependen del marco de referencia porque el tiempo no se desarrolla de la misma manera dependiendo del marco de referencia.

La medición del tiempo, transformada en una medición de distancia, puede asociarse con las otras tres coordenadas del espacio. Así, todas las mediciones están en unidades de distancia. ¡El tiempo se ha convertido en espacio!

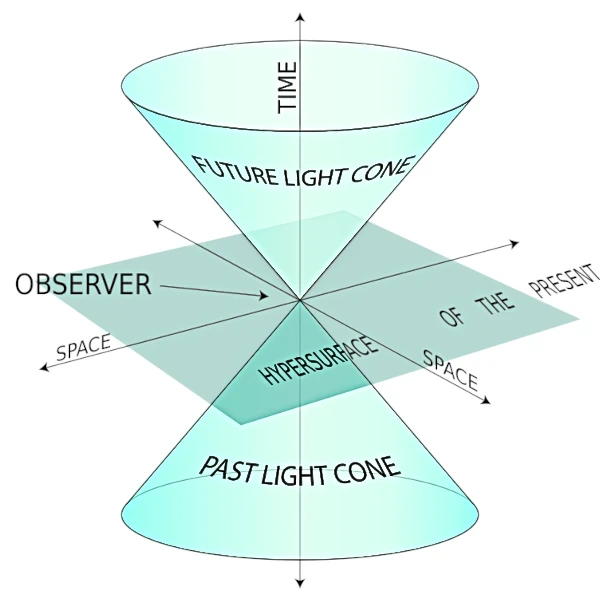
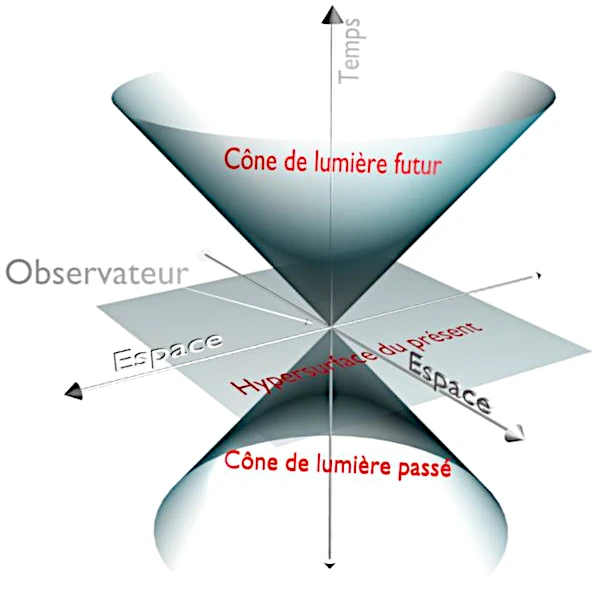
Todos los eventos puntuales están conectados a la velocidad de la luz. El conjunto de todos los eventos se llama "espacio-tiempo". La frontera definida por el cono de luz se llama "horizonte cosmológico".

Las líneas de universo que definen el cono pueden describirse mediante una partícula que se mueve a la velocidad de la luz, lo que define la frontera del cono. La representación de las líneas de universo en la parte inferior (cono invertido) se debe al hecho de que un evento también puede tener un pasado. Si el objeto está estacionario en el espacio-tiempo, no se mueve en el espacio, pero se mueve en el tiempo (eje vertical).

Si el objeto está en movimiento, necesariamente a una velocidad menor que c, el desplazamiento tendrá lugar dentro del cono de luz que tiene el origen como su vértice (el presente). La línea de universo de un personaje en movimiento tiene un ángulo en el cono que depende de su velocidad; se mueve en el espacio y el tiempo. Los bordes del cono definen la velocidad límite, la de las partículas de luz. La superficie del cono está reservada para la representación de la propagación de las señales de luz emitidas por el objeto.

El interior del cono de luz superior (lado positivo) representa "el futuro". El vértice del cono de luz representa "aquí y ahora". El interior del cono de luz inferior (lado negativo) representa "el pasado". El exterior del cono no es accesible por una señal de luz porque iría más rápido que la velocidad de la luz. El exterior representa "otro lugar".

Un cuerpo del mundo real tiene una línea de universo en el espacio-tiempo. El conjunto de su historia (todos los eventos de su vida) traza esta línea. En el universo euclidiano de cuatro dimensiones de Minkowski, las trayectorias de los objetos en el espacio-tiempo son siempre líneas rectas.

Lo que hay que recordar

La comprensión de la relatividad especial está lejos de ser inmediata; se requiere mucha imaginación para entender los conceptos ocultos detrás de la ecuación E=mc². Muchos físicos contribuyeron a la emergencia de esta fórmula en la mente de Einstein.

• Galileo (1564-1642) por la relatividad galileana y el sistema de referencia en movimiento uniforme.
• Isaac Newton (1642-1727) por sus leyes del movimiento.
• Michael Faraday (1791-1867) por su trabajo sobre la electricidad y el magnetismo.
• James Clerk Maxwell (1831-1879) por unificar la electricidad y el magnetismo e integrar la luz en el fenómeno electromagnético.
• George Fitzgerald (1851-1901) por la contracción de longitudes.
• Hendrik Antoon Lorentz (1853-1928) por la contracción de longitudes y la dilatación del tiempo.
• Henri Poincaré (1854-1912) por la estructura de grupo de las transformaciones de Lorentz.
• Albert Abraham Michelson (1852-1931) y Edward Williams Morley (1838-1923) por el experimento sobre la invariancia de la velocidad de la luz en el éter luminífero.

• Para Einstein, la luz consiste en fotones; no hay necesidad de éter luminífero.
• Existe una velocidad límite que los objetos no pueden exceder. Esta velocidad vincula la masa y la energía.
• c ya no es la velocidad de un objeto sin masa, sino que se convierte en una constante universal de la física que encontramos en todos los fenómenos.
• A la velocidad de la luz, el tiempo ya no fluye. No hay velocidad cero; no hay un marco de referencia absoluto. La idea de inmovilidad no existe.
• La simple aplicación del factor de Lorentz explica la invariancia de la velocidad de la luz y su límite, la dilatación del tiempo y la contracción de longitudes.
• La energía y la materia son de la misma naturaleza. Para que la energía se convierta en masa, se necesita mucha energía; para que la masa se convierta en energía, se necesita muy poca masa. La masa de un cuerpo representa el contenedor de energía.
• La materia y la antimateria, al encontrarse, se aniquilan y transforman el 100% de su masa en energía pura.
• El continuo espacio-tiempo tiene cuatro dimensiones. Tres dimensiones para el espacio (x, y, z) y una para el tiempo (ct), que se transforma en una distancia asociándola con la constante c (d=ct). En el espacio-tiempo, el tiempo está geometrizado.
• Con esta misteriosa fórmula E=mc² que desafía el sentido común, Albert Einstein puso todo el universo en una ecuación, desde lo infinitamente grande hasta lo infinitamente pequeño. E=mc² une la cosmología y la física cuántica. Si esta ecuación fuera refutada, toda nuestra física se derrumbaría.