Atom: Atomic Orbitals

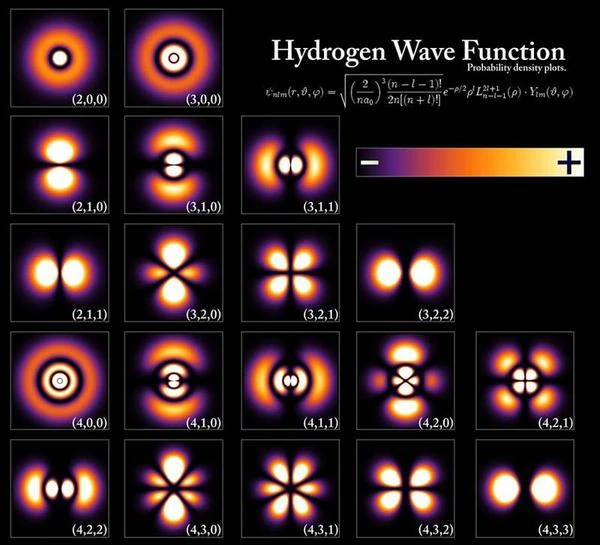
Description of the image: The atomic orbitals of the hydrogen atom are represented according to the electron's energy and angular momentum. The energy level increases from top to bottom (n = 1, 2, 3, 4, 5) and the angular momentum increases from left to right (l = s, p, d, f, g). Colors: Black: zero probability density (the electron never goes there). White: maximum density (the electron frequently passes through). Red-orange: intermediate density. Quantum numbers: n: principal quantum number, defines the energy level. l: secondary or orbital quantum number, defines the subshells (s, p, d, f, g...). m: magnetic quantum number, represents the orientations of the atomic orbitals. s: spin quantum number, quantifies the intrinsic "angular momentum" of the electron. This representation shows the probability density of finding the electron in different regions around the nucleus. Image source: GNU Free Documentation License.

Structure of the Atom

It is by examining the smallest constituents of matter that scientists (20th century) will explain the functioning of the entire universe.

An atom consists of a nucleus around which one or more electrons move. What characterizes the nucleus is its number of protons (Z), which ranges from 1 to 110, determining the element, for example, iron (Fe26) has 26 protons, 26 is its atomic number (Z). The number of neutrons (N), ranging from 0 to 160, characterizes the isotopes of the element, for example, hydrogen (H1) has one proton and no neutrons, deuterium (H2) has one proton and one neutron, tritium (H3) has one proton and two neutrons.

These three forms of hydrogen have only one electron since there is only one electrical charge, the single proton.

Note that only in the case of hydrogen are different names given to the isotopes of the element; in all other cases, only the number of nucleons is indicated, which allows the number of neutrons to be determined. For example, iron (Fe26) has several isotopes, including Fe56, which has 30 neutrons, Fe57 has 31 neutrons, Fe58 has 32 neutrons, the number of neutrons differentiates the isotopes.

In the atom, it is the electrons that give matter its consistency, yet it is very light (≈10^-27 g). The proton is ≈2000 times heavier and concentrates most of the mass of the atom (99.99%). For stable atoms, the mass ranges between 1.674×10^-24 g for Hydrogen and 3.953×10^-22 g for Uranium.

Since 1811, we have known the approximate size of an atom; Amedeo Avogadro (1776-1856) estimated the size of atoms to be 10-10 meters (Angstrom), i.e., a little more than one-hundred-thousandth of a millimeter. In 1911, Ernest Rutherford (1871-1937) discovered the atomic nucleus.

Rutherford specified the structure of the atom by bombarding a gold foil with particles from the radioactive decay of uranium. He gave a size to the atomic nucleus of the order of 10^-14 meters.

Rutherford represented each atom as a mini solar system, with the nucleus at the center and electrons orbiting like planets.

Since the advent of quantum mechanics (1920s), the image of the nucleus is troubling; the nucleus is no longer a system composed of corpuscles associated together. The nucleus, governed by quantum mechanics, is not observable because to observe the nucleons inside the nucleus, one would need to illuminate the particles with such intense light that the nucleus would instantly disintegrate.

The same is true for the electron; we no longer represent the electron as a corpuscle orbiting a well-defined path around the nucleus. The electron is neither a wave nor a corpuscle; however, we speak of wave-particle duality, which is the foundation of quantum mechanics. The electron does not follow a single trajectory; it is probably located in a region around the nucleus called the atomic orbital.

Electron Cloud or Atomic Orbital

Since 1924, all matter has been endowed with an associated wave, according to the hypothesis of Louis De Broglie (1892-1987). With this hypothesis, he generalized the "wave-particle duality" introduced for light by Max Planck (1858-1947) at the beginning of the 20th century to all particles of matter.

All subatomic particles therefore have a wavelength. The wavelength λ of a subatomic particle and its momentum p are related by the equation: λ=h/p, where h is Planck's constant, p is the momentum, i.e., the product of mass and velocity vector (p=mv). The electron takes about 150 attoseconds (1.5×10⁻¹⁶ seconds) to "orbit" the hydrogen atom.

Thanks to Einstein's formula (E=mc2), all matter is endowed with associated energy. In other words, the smaller the wavelength, the higher the energy (E=h/λ). This energy will modify the shape of atoms. The foundations of quantum mechanics are thus laid.

What Do the Particles of the Infinitely Small World Look Like?

Matter is composed of very small particles (electrons, neutrinos, quarks) that have mass, charge, energy, dimension, wave, and spin.

In 2013, we still cannot see the particles of the atomic nucleus but only the outer layer of the atom, i.e., its electron cloud. The electron cloud occupies the entire spatial extent of the atom since it is about 10,000 times larger than its nucleus.

In wave quantum mechanics, a particle is represented by a wave function (state vector), but it is very difficult to conceptualize the fundamental concept of quantum mechanics or the quantum state of a system.

In 1927, Max Born (1882-1970) gave an interpretation of the wave function where the square of the wave function represents the probability of finding the particle in a precise location when a measurement is made.

A wave function is therefore a probability amplitude or a probability density of the presence of the system in a given position at a given time. This function has a complex value. If a real number or real value represents, for example, the length of a segment on a line, a complex value is represented by a vector in a plane. This vector has not only a length in space but also a phase corresponding to the direction of the vector.

If we no longer represent the electron as a point particle on a regular orbit around a nucleus, how can we visualize it?

The electron does not follow a single trajectory around the nucleus; it is located somewhere in a "vast region" called the electron cloud or atomic orbital. The state of an electron is therefore represented by this volume of space around the nucleus in which it is delocalized. The ground state of a hydrogen atom measures about 1 angstrom, i.e., 10^-10 meters.

To visualize the electron in this region, simply imagine a grain of rice about 5 mm moving in a sphere about 50 meters in diameter. But it is not always a sphere; the shape of this region of atomic space depends on the electron's energy and angular momentum.

The electron's orbitals can take on different characteristic shapes depending on the nature of the atom, for example, the orbital of the hydrogen atom in the first row at the top of the image has a spherical shape, the orbital in the second row has the shape of two water droplets, the orbital in the third row has the shape of four water droplets. In summary, the orbital corresponds to the region of space where the electron is delocalized; the state of the electron is in a superposition of all possible positions within the atomic orbital, whose shape varies. The shape of the orbital changes when the atom is excited, as in the first row. If the atom is excited further, the shape of the orbital changes again, as in the second row or second electron shell. In a highly excited state called the "Rydberg state," the electrons are delocalized in a torus of "very large radius" that can measure up to 1000 angstroms; the principal quantum number n (shell number) is very high, between 50 and 100.

N.B.: An electron, attracted by the positive charge of the nucleus, cannot "stick to the nucleus" because that would mean that the spatial extension of its wave function is reduced to a point (without velocity or angular momentum). Schrödinger's equation states that an electron, in the vicinity of the nucleus, is in an orbital with a geometry determined by the quantum numbers that satisfy this equation. In short, an electron is confined in the vicinity of the nucleus by the electrostatic potential well. When the potential energy is increasing, it is said that the particle is moving in a potential well.