From the Ancient Atom to the Modern Atom: An Exploration of Atomic Models

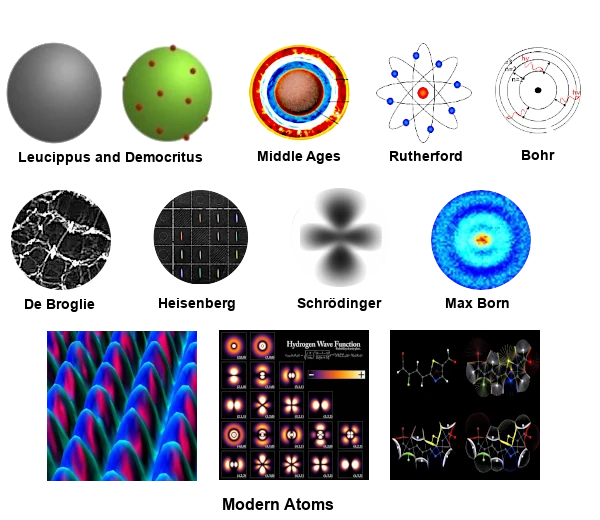
Description of the image: Atomic Models Through the Ages: From Democritus to Schrödinger. Image source: Astronoo.

Nature of the Atom in the Atomist School

In antiquity, the atomist school was one of the first attempts to understand the nature of matter through corpuscles called 'atomos' (indivisible).

Two Greek philosophers of the atomist school, Leucippus (500 - 440 BC) and Democritus (460 - 370 BC) thought that all matter is composed of tiny corpuscles, in perpetual motion, very solid and eternal.

Their conception of atoms was a philosophical abstraction based on logic: if one imagines continuously cutting an object, can it be divided infinitely?

Democritus thought that atoms differed in shape, size, position, and orientation. For example, he imagined that the atoms that make up liquids would be smooth and round to slide easily over each other, while those of solids would be rough and hooked to interlock.

Movement of the Atom in the Atomist School

In the atomist school of Leucippus and Democritus, the atom is in perpetual rectilinear motion in the void, influenced by the clinamen. The clinamen is a slight random deviation in the motion of atoms that allows for the emergence of diversity in the material world.

Nature of the Atom in the Middle Ages

During the Middle Ages, the atomist ideas of Leucippus, Democritus, and Epicurus were largely rejected by philosophers and theologians. This period was dominated by the Aristotelian view of matter.

Aristotle (4th century BC) rejected the idea of atoms and the void. He proposed that all matter was composed of four fundamental elements: earth, water, air, and fire, associated with qualities (hot, cold, dry, humid). Matter was considered continuous, without indivisible corpuscles.

Movement of the Atom in the Middle Ages

In the Middle Ages, the movement of atoms did not really exist in philosophical discourse. Movement was generally seen as a transformation of the elements according to internal qualities or external influences.

Nature of the Atom According to Ernest Rutherford

In 1911, the experiment of Ernest Rutherford (1871-1937) revolutionized our understanding of the atom by demonstrating the existence of a dense central nucleus.

Rutherford proposed a model of the atom, also known as the planetary model, where a dense and massive central nucleus, positively charged, contains almost all the mass of the atom.

Light electrons orbit around the nucleus at a certain distance, in what can be compared to an orbit, although their exact motion is not yet well defined.

N.B.: Rutherford developed his model using a thin gold foil bombarded by alpha particles (helium nuclei). Most particles pass without deflection, showing that the atom is mostly empty. Some particles are strongly deflected, and some almost directly rebound, proving the presence of a dense and positive nucleus.

Orbits of Electrons in Rutherford's Atom

Rutherford's model has a simplified view of the motion of electrons around the nucleus. It is stable, circular, and dictated by the electrostatic force of attraction between the nucleus and the electrons. This model does not explain why electrons do not lose energy and fall into the nucleus (which classical physics predicts).

Nature of the Atom According to Niels Bohr

In 1913, the model of Niels Bohr (1885-1962) introduced the quantization of electron orbits, marking a crucial step in the understanding of the atom.

Niels Bohr represents a fundamental step in the history of atomic physics, as he introduced a quantized description of the motion of electrons in an atom, based on classical mechanics and the first ideas of quantum mechanics.

What distinguishes Bohr's model from classical theories is the idea that only certain orbits are allowed. These orbits are quantized, meaning that electrons can only occupy specific energy levels. Electrons emit or absorb a well-defined amount of energy, in the form of light quanta, during transitions between orbits.

Bohr's model successfully explained phenomena such as the spectroscopy of hydrogen, showing that spectral lines are due to transitions between quantized energy levels. Unfortunately, this model only works well for hydrogen (a single electron) and fails for more complex atoms. It does not explain the spectra of multi-electron atoms.

Quantized Orbits of Electrons in Bohr's Atom

Bohr assumes that electrons move in circular orbits around the nucleus. Each orbit corresponds to a specific energy level. During this motion, nothing happens, unlike classical mechanics, where an electron in motion around the nucleus should lose energy and collapse into the nucleus.

Bohr's model postulates that electrons in stable orbits do not lose energy and remain in these orbits without collapsing. However, electrons can transition from one energy level to another by absorbing or emitting quanta of energy (what we now call a photon). Quantum jumps are not considered continuous movements.

Nature of the Atom According to Louis De Broglie

In 1924, the theory of De Broglie (1892-1987) introduced the wave-particle duality, a fundamental notion of quantum mechanics.

The central idea of De Broglie's theory is that if light behaves as both a wave and a particle, then any material particle (such as electrons) can behave both as a wave and as a particle, a concept known as wave-particle duality.

Massive particles, such as electrons, possess an associated wavelength called the De Broglie wavelength. De Broglie's model provides a physical justification based on wave-particle duality.

De Broglie suggests that electrons orbiting the nucleus should be considered not as point particles following classical circular trajectories, but as standing waves, and their probable positions are distributed in such a way as to correspond to constructive interference. This model is a fundamental step in the transition from a classical view of the atom (Bohr) to a fully quantum description integrated into Schrödinger's wave mechanics.

Standing Waves and Quantum Orbitals in De Broglie's Atom

The motion of electrons in De Broglie's atom does not correspond to a defined trajectory but rather to a wave distribution around the nucleus. Electrons behave as standing circular waves. They do not follow classical trajectories but occupy regions of space corresponding to quantum orbitals.

Nature of the Atom According to Werner Heisenberg

In 1925, the model of Werner Heisenberg (1901-1976) introduced a probabilistic description of the atom, marking a break with classical models.

The model of the atom proposed by Heisenberg, known as matrix mechanics, is one of the first formulations of quantum mechanics. Unlike Bohr's model, which describes electrons as moving in well-defined circular orbits, Heisenberg's model introduces a more abstract and mathematical description of the states and transitions of electrons.

Heisenberg transformed the image of the atom from a classical one to a deeply abstract conception where quantum reality is no longer deterministic but based on probabilities. The atom is a probabilistic entity governed by statistical laws where its measurable properties (energy, position, velocity, etc.) emerge only when an observation interaction occurs (an act of measurement).

Heisenberg's atom is presented as a dense nucleus consisting only of protons (identified in 1919), surrounded by diffuse clouds representing the probability of the presence of electrons. These clouds can take different shapes, depending on the orbitals.

However, the stability of the atom remained problematic without a clear explanation to neutralize electrostatic repulsions.

Quantum States and Transitions in Heisenberg's Atom

The movements of electrons are described abstractly and mathematically by state vectors and matrix operators. Electrons do not have well-defined classical trajectories but exist in superposed quantum states.

Transitions between these states are quantized and probabilistic. Heisenberg's uncertainty principle plays a fundamental role in this description, limiting the precision with which the position and momentum of electrons can be known simultaneously.

Nature of the Atom According to Erwin Schrödinger

In 1926, the equation of Erwin Schrödinger (1887-1961) allowed the description of the quantum states of electrons, marking a major advance in quantum mechanics.

The model of the atom proposed by Schrödinger, known as wave mechanics, is another fundamental formulation of quantum mechanics. Schrödinger introduced the equation that bears his name to describe the behavior of quantum particles such as electrons in an atom. With his equation, Schrödinger can precisely calculate the vibration of this wave and thus the light it emits, retrieving the correct spectrum as in Heisenberg's theory.

In Schrödinger's model, the state of an electron is described by a wave function (Ψ) that contains all possible information about the quantum state of the electron.

The wave function is not directly observable, but its square gives the probability density of finding the electron at a certain position in space. This means that the electron does not have a defined position but rather a distribution of probability of presence.

These regions of probability are called atomic orbitals. It was Max Born (1882-1970) who proposed the probabilistic interpretation of the wave function in 1926. This interpretation allowed for the understanding of atomic orbitals as regions of space where the probability of finding an electron is high.

Wave Functions and Atomic Orbitals in Schrödinger's Atom

The "movements" of electrons are described by wave functions that represent distributions of probability of presence in atomic orbitals.

Electrons do not have well-defined classical trajectories but exist in superposed quantum states. Transitions between energy levels are described by changes in the wave function, and the temporal evolution of the wave function is continuous and deterministic. It describes probabilities rather than classical movements.

Nature of the Atom According to Max Born

In 1926, the probabilistic interpretation of Max Born allowed for the understanding of atomic orbitals as regions of probability.

Max Born interpreted the wave function ψ (solution of Schrödinger's equation) not as a material or physical wave, but as a probability amplitude. More precisely, he proposed that the probability density of finding a particle (such as an electron) at a given position is proportional to the absolute square of the wave function.

The atom according to Max Born marks a complete break with classical conceptions: it becomes an entity where notions of trajectory, precise position, and determinism are abandoned in favor of a statistical and probabilistic description based on wave functions. This vision constitutes one of the fundamental bases of the nature of the modern atom.

Probability Clouds and Quantum Indeterminism in Born's Atom

In Born's atom, electrons do not follow classical trajectories as in the models of Rutherford or Bohr. Their exact position at any given moment is fundamentally indeterminate. Instead of precise trajectories, we speak of probability clouds where the density of the cloud represents the probability of the presence of the electron.

Born demonstrates that electrons do not follow continuous and deterministic trajectories. This behavior is directly linked to the quantum indeterminism introduced by Heisenberg's uncertainty principle.

Nature of the Modern Atom

The modern view of the atom integrates advanced concepts such as spin, spin-orbit interactions, and relativistic effects.

The nature of the modern atom is described by quantum mechanics, which offers a much more complex and nuanced view than semi-classical models such as those of Rutherford, Bohr, Heisenberg, or Schrödinger.

The modern view includes the spin of the electron and spin-orbit interactions, as well as quantum field theory to describe the interactions between particles and fields, including relativistic effects and electromagnetic interactions. QFT is essential for understanding high-energy phenomena and fundamental interactions.

Furthermore, it integrates the Pauli exclusion principle, which states that two electrons in the same atom cannot have the same set of quantum numbers. This explains the shell structure of atoms and the periodicity of elements in the periodic table.

Complex Interactions and Relativistic Effects in the Modern Atom

In the modern atom, the concept of "movement" of electrons is effectively very different from that of classical models. Rather than speaking of well-defined trajectories, we speak of probability distributions and quantum states.

Conclusion

The modern atom cannot be imaged classically due to its probabilistic and non-local nature. However, symbolic and schematic representations can help visualize certain aspects of the modern atom. Atomic orbitals, probability clouds, and energy levels can provide a more complete image of the modern atom.

N.B.: The term "non-local" in the context of quantum mechanics and the modern atom refers to a phenomenon where the properties of a particle can be instantaneously influenced by events occurring at an arbitrary distance, without any classical means of information transmission.