Tunneling Effect: Exploring the Invisible Atom by Atom

Tunneling Effect: A Counterintuitive but Real Phenomenon

In classical mechanics, a particle facing a potential barrier higher than its energy is inevitably reflected. However, in the quantum world, the rules are different: a particle has a non-zero probability of traversing such a barrier. This is the famous tunneling effect. This phenomenon directly results from the wave-like nature of particles described by Schrödinger's equation.

Mathematically, the wave function $\psi(x)$ of a particle in a classically forbidden region (where $E › V(x)$) does not vanish but decreases exponentially: $$ \psi(x) \sim e^{-\kappa x}, \quad \text{with } \kappa = \sqrt{\\frac{2m(V_0 - E)}{\hbar^2}}. $$ Thus, even if the probability density is very low, it is not zero, allowing the particle to "pierce" the barrier.

Practical Applications of the Tunneling Effect

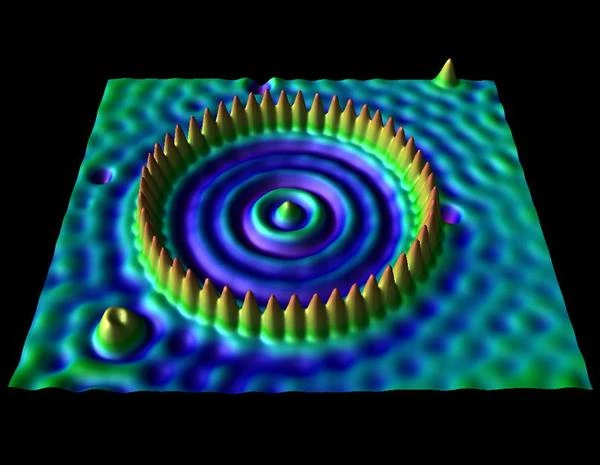
The tunneling effect is not just a theoretical concept; it has major technological applications. The most emblematic example is scanning tunneling microscopy (STM), which allows surfaces to be observed with atomic resolution. In this device, a tunneling current is measured between a conductive tip and the surface of a sample, separated by only a few angstroms.

Another example is the tunnel transistor and Josephson junctions in superconducting circuits, where the tunneling effect allows Cooper pairs to pass through an insulating barrier, a phenomenon crucial for the development of quantum computers.

Even at the nuclear level, this effect explains alpha decay, where an alpha particle escapes the atomic nucleus by crossing a nuclear potential barrier.

Tunneling Effect: A Window into the Probabilistic Nature of the Quantum World

The tunneling effect challenges our intuition based on classical causality. It reveals that in the quantum world, there is no deterministic trajectory. Quantum mechanics only provides probabilities. The very existence of this phenomenon is experimental proof that particles are not localized objects but entities governed by probability amplitudes.

In short, the tunneling effect is one of the most surprising jewels of modern physics. It perfectly illustrates how the rules of quantum mechanics defy our intuitive understanding of the world while having concrete repercussions in advanced technologies.

The Scanning Tunneling Microscope (STM)

The Scanning Tunneling Microscope: A Window into the Quantum World

The scanning tunneling microscope, invented in 1981 by Gerd Binnig (1947-) and Heinrich Rohrer (1933-2013), Nobel laureates in 1986, is directly based on the phenomenon of quantum tunneling. In an STM, a very fine metal tip is brought to within a nanometer of a conductive surface. When a voltage is applied between the tip and the sample, a tunneling current appears, even though the two are not in physical contact. This current is extremely sensitive to the distance between the tip and the surface (exponentially decreasing), allowing the electronic topography to be mapped with a lateral resolution of less than 0.1 nm.

The operation relies on the local density of electronic states (LDOS) of the sample, accessible through the measured tunneling current. By maintaining a constant current via a feedback system, the vertical position of the tip reveals the atomic topography of the surface. Thus, the STM allows individual atoms to be "seen," making it a fundamental tool in condensed matter physics, nanotechnology, and surface chemistry.