Tunneleffekt: Erforschung des unsichtbaren Atoms von Atom

Tunneleffekt: Ein kontraintuitives, aber reales Phänomen

In der klassischen Mechanik wird ein Teilchen, das einer potenziellen Barriere gegenübersteht, die höher als seine Energie ist, zwangsläufig reflektiert. In der Quantenwelt gelten jedoch andere Gesetze: Die Wahrscheinlichkeit, dass ein Teilchen eine solche Barriere überschreitet, ist ungleich Null. Dies ist der berühmte Tunneleffekt. Dieses Phänomen ergibt sich direkt aus der Wellennatur von Teilchen, die durch die Schrödinger-Gleichung beschrieben wird.

Mathematisch gesehen verschwindet die Wellenfunktion $\psi(x)$ eines Teilchens in einem klassisch verbotenen Bereich (wobei $E › V(x)$) nicht, sondern zerfällt exponentiell: $$ \psi(x) \sim e^{-\kappa x}, \quad \text{with } \kappa = \sqrt{\\frac{2m(V_0 - E)}{\hbar^2}}. $$ Selbst wenn die Wahrscheinlichkeitsdichte sehr niedrig ist, ist sie daher nicht Null, was es dem Teilchen ermöglicht, die Barriere zu „durchdringen“.

Konkrete Anwendungen des Tunneleffekts

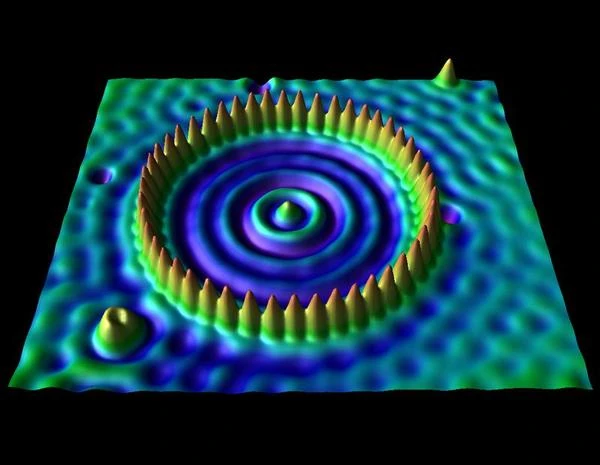
Der Tunneleffekt ist kein einfaches theoretisches Konzept: Er hat große technologische Anwendungen. Das symbolträchtigste Beispiel ist dasRastertunnelmikroskopie (STM), wodurch Oberflächen mit atomarer Auflösung beobachtet werden können. Bei diesem Gerät wird ein Tunnelstrom zwischen einer leitenden Spitze und der Oberfläche einer Probe gemessen, die nur wenige Angström voneinander entfernt sind.

Ein weiteres Beispiel: dieTunneleffekttransistorund dieJosephson-Kreuzungenin supraleitenden Schaltkreisen, wo der Tunneleffekt den Durchgang von Cooper-Paaren durch eine isolierende Barriere ermöglicht, ein entscheidendes Phänomen für die Entwicklung von Quantencomputern.

Selbst auf nuklearer Ebene erklärt dieser Effekt dasAlpha-Zerfall, bei dem ein Alphateilchen aus dem Atomkern entweicht, indem es eine nukleare Potentialbarriere überschreitet.

Tunneleffekt: Ein Fenster in die probabilistische Natur der Quantenwelt

Der Tunneleffekt stellt unsere auf klassischer Kausalität basierende Intuition in Frage. Es zeigt, dass es in der Quantenwelt keine deterministische Flugbahn gibt. Die Quantenmechanik liefert nur Wahrscheinlichkeiten. Die bloße Existenz dieses Phänomens ist ein experimenteller Beweis dafür, dass Partikel keine lokalisierten Objekte sind, sondern Einheiten, die durch Wahrscheinlichkeitsamplituden bestimmt werden.

Kurz gesagt, der Tunneleffekt ist eines der überraschendsten Juwelen der modernen Physik. Es veranschaulicht perfekt, wie die Regeln der Quantenmechanik unser intuitives Verständnis der Welt herausfordern und gleichzeitig konkrete Auswirkungen auf fortschrittliche Technologien haben.

Das Rastertunnelmikroskop (STM)

Das Tunnelmikroskop: Ein Fenster zur Quantenwelt

Das Rastertunnelmikroskop, 1981 erfunden vonGerd Binnig(1947-) undHeinrich Rohrer(1933-2013), Nobelpreis 1986, basiert direkt auf dem Phänomen des Quantentunnelns. Bei einem STM wird eine sehr feine Metallspitze in einem Abstand von etwa einem Nanometer von einer leitenden Oberfläche angefahren. Wenn zwischen der Spitze und der Probe eine Spannung angelegt wird, entsteht ein Tunnelstrom, obwohl die beiden keinen physischen Kontakt haben. Dieser Strom reagiert äußerst empfindlich auf den Abstand zwischen Spitze und Oberfläche (exponentiell abnehmend), sodass die elektronische Topographie mit einer lateralen Auflösung von weniger als 0,1 nm kartiert werden kann.

Der Betrieb basiert auf der lokalen elektronischen Zustandsdichte (LDOS) der Probe, die durch den gemessenen Tunnelstrom zugänglich ist. Durch die Aufrechterhaltung eines konstanten Stroms über ein Rückkopplungssystem zeigt die vertikale Position der Spitze die atomare Topographie der Oberfläche. Somit ermöglicht STM das individuelle „Sehen“ von Atomen, was es zu einem grundlegenden Werkzeug in der Physik der kondensierten Materie, der Nanotechnologie und der Oberflächenchemie macht.