Die Entwicklung der Atommodelle: von der Antike bis zur Gegenwart

Bildbeschreibung: Atommodelle im Wandel der Zeit: Von Demokrit bis Schrödinger. Bildquelle:astronoo.com

Natur des Atoms aus der Atomschule

In der AntikeDie Schule der Atomisten ist einer der ersten Versuche, die Natur der Materie mithilfe von Korpuskeln zu verstehen, die „Atomos“ (unteilbar) genannt werden.

Zwei griechische Philosophen der Atomschule,Leukipp(500 - 440 v. Chr.) undDemokrit(460 - 370 v. Chr.) glauben, dass alle Materie aus winzigen Teilchen besteht, die sich in ständiger Bewegung befinden, sehr fest und ewig sind.

Ihre Vorstellung von Atomen war aphilosophische AbstraktionBasierend auf der Logik: Wenn wir uns vorstellen, ein Objekt kontinuierlich zu schneiden, können wir es dann unendlich teilen?

Demokrit glaubte, dass sich Atome in Form, Größe, Position und Ausrichtung unterschieden. Er stellte sich zum Beispiel vor, dass die Atome, aus denen Flüssigkeiten bestehen, glatt und rund wären, um leicht aneinander vorbeizugleiten, während die Atome von Festkörpern rau und hakenförmig wären und sich ineinander verflechten würden.

Bewegung des Atoms der Atomschule

In der Atomschule von Leukipp und Demokrit befindet sich das Atom in einem Vakuum in ständiger geradliniger Bewegung, beeinflusst vonclinamen. Das Klinamen ist eine leichte zufällige Abweichung in der Bewegung von Atomen, die die Entstehung von Vielfalt in der materiellen Welt ermöglicht.

Natur des Atoms im Mittelalter

Im MittelalterDie atomistischen Ideen von Leukipp, Demokrit und Epikur wurden von Philosophen und Theologen weitgehend abgelehnt. Diese Zeit wurde von der aristotelischen Sicht der Materie dominiert.

Aristoteles (4. Jahrhundert v. Chr.) lehnte die Idee von Atomen und der Leere ab. Er schlug vor, dass alle Materie aus vier Grundelementen bestehe:Erde, L'Wasser, L'Luftund dieFeuer, verbunden mit Eigenschaften (heiß, kalt, trocken, feucht). Materie galt als kontinuierlich, ohne unteilbare Teilchen.

Bewegung des Atoms im Mittelalter

Im Mittelalter existierte die Bewegung von Atomen im philosophischen Diskurs nicht wirklich. Bewegung wurde im Allgemeinen als Transformation von Elementen aufgrund innerer Qualitäten oder äußerer Einflüsse angesehen.

Die Natur des Atoms von Ernest Rutherford

Im Jahr 1911, die Erfahrung vonErnest Rutherford(1871-1937) revolutionierte unser Verständnis des Atoms, indem er die Existenz eines dichten zentralen Kerns nachwies.

Rutherford schlug ein Modell des Atoms vor, auch genanntPlanetenmodellwo ein dichter und massiver zentraler Kern, positiv geladen, fast die gesamte Masse des Atoms enthält.

Leichte Elektronen umkreisen den Kern in einiger Entfernung, was mit einer Umlaufbahn verglichen werden kann, obwohl ihre genaue Bewegung noch nicht genau definiert ist.

Hinweis: :
Rutherford entwickelte sein Modell unter Verwendung einer dünnen Goldschicht, die mit Alphateilchen (Heliumkernen) beschossen wurde. Die Mehrzahl der Teilchen passiert ohne Abweichung, was zeigt, dass das Atom größtenteils leer ist. Einige Teilchen werden stark abgelenkt, andere prallen fast direkt zurück, was das Vorhandensein eines dichten, positiven Kerns beweist.

Elektronenbahnen im Rutherford-Atom

Das Rutherford-Modell bietet eine vereinfachte Sicht auf die Bewegung von Elektronen um den Kern. Es ist stabil, kreisförmig und wird durch die elektrostatische Anziehungskraft zwischen dem Kern und den Elektronen bestimmt. Dieses Modell kann nicht erklären, warum Elektronen keine Energie verlieren und in den Kern fallen (was die klassische Physik vorhersagt).

Die Natur des Atoms von Niels Bohr

Im Jahr 1913, das Modell vonNiels Bohr(1885-1962) führte die Quantifizierung elektronischer Umlaufbahnen ein und markierte damit einen entscheidenden Schritt zum Verständnis des Atoms.

Niels Bohr stellt einen grundlegenden Schritt in der Geschichte darAtomphysik, weil es eine quantifizierte Beschreibung der Bewegung von Elektronen in einem Atom einführt, basierend aufklassische Mechanikund die ersten Ideen derQuantenmechanik.

Was zeichnet die ausBohr-ModellEine der klassischen Theorien ist die Idee, dass nur bestimmte Umlaufbahnen erlaubt sind. Diese Umlaufbahnen sind quantisiert, was bedeutet, dass Elektronen nur bestimmte Energieniveaus einnehmen können. Elektronen emittieren oder absorbieren eine genau definierte Energiemenge in Form vonLichtquant, während Übergängen zwischen Umlaufbahnen.

Bohrs Modell konnte Phänomene wie erfolgreich erklärenWasserstoffspektroskopie, indem man zeigt, dass dieSpektralliniensind auf Übergänge zwischen quantisierten Energieniveaus zurückzuführen. Leider lässt sich dieses Modell nur gut auf Wasserstoff (ein einzelnes Elektron) anwenden und versagt bei komplexeren Atomen. Es erklärt nicht die Spektren von Mehrelektronenatomen.

Quantisierte Elektronenbahnen im Bohr-Atom

Bohr geht davon aus, dass sich Elektronen auf Kreisbahnen um den Kern bewegen. Jede Umlaufbahn entspricht einem bestimmten Energieniveau. Während dieser Bewegung passiert nichts, anders als bei der klassischen Mechanik, bei der ein Elektron, das sich um den Kern bewegt, Energie verlieren und auf den Kern kollabieren sollte.

Das Bohr-Modell geht davon aus, dass Elektronen in stabilen Umlaufbahnen keine Energie verlieren und in diesen Umlaufbahnen bleiben, ohne zu kollabieren. Elektronen können sich jedoch von einem Energieniveau in ein anderes bewegen, indem sie Energiequanten (was wir heute als Photonen bezeichnen) absorbieren oder abgeben. Quantensprünge gelten nicht als kontinuierliche Bewegungen.

Die Natur des Atoms von Louis De Broglie

Im Jahr 1924, die Theorie vonDe Broglie(1892-1987) führte den Welle-Teilchen-Dualismus ein, einen Grundbegriff der Quantenmechanik.

Die zentrale Idee von de Broglies Theorie besteht darin, dass, wenn sich Licht wie eine Welle und ein Körper verhält, jedes materielle Teilchen (z. B. Elektronen) sich sowohl als Welle als auch als Körper verhalten kann, ein Konzept, das als Welle-Teilchen-Dualität bezeichnet wird.

Massive Teilchen wie Elektronen haben eine zugehörige Wellenlänge, die De-Broglie-Wellenlänge genannt wird. Das Modell von De Broglie liefert eine physikalische Begründung, die auf dem Welle-Teilchen-Dualismus basiert.

De Broglie schlägt vor, dass die den Kern umkreisenden Elektronen nicht als Punktteilchen betrachtet werden sollten, die klassischen Kreisbahnen folgen, sondern als stehende Wellen und ihre wahrscheinlichen Positionen so verteilt, dass sie konstruktiver Interferenz entsprechen. Dieses Modell ist ein grundlegender Schritt beim Übergang von einer klassischen Vision des Atoms (Bohr) zu einer vollständigen Quantenbeschreibung, die in Schrödingers Wellenmechanik integriert ist.

Stehende Wellen und Quantenorbitale im De-Broglie-Atom

Die Bewegung der Elektronen im De-Broglie-Atom entspricht keiner definierten Flugbahn, sondern einer Wellenverteilung um den Kern. Elektronen verhalten sich wie stehende Kreiswellen. Sie folgen keinen klassischen Flugbahnen, sondern besetzen Raumregionen, die Quantenorbitalen entsprechen.

Die Natur des Atoms von Werner Heisenberg

Im Jahr 1925, das Modell vonWerner Heisenberg(1901-1976) führte eine probabilistische Beschreibung des Atoms ein und markierte damit einen Bruch mit klassischen Modellen.

Das von Heisenberg vorgeschlagene Atommodell, bekannt alsMatrixmechanikist eine der ersten Formulierungen der Quantenmechanik. Im Gegensatz zu Bohrs Modell, das Elektronen als Bewegungen auf wohldefinierten Kreisbahnen beschreibt, führt Heisenbergs Modell eine abstraktere und mathematischere Beschreibung von Elektronenzuständen und -übergängen ein.

Heisenberg verwandelte das Bild des Atoms von einem klassischen Bild in eine zutiefst abstrakte Vorstellung, in der die Quantenrealität nicht mehr deterministisch ist, sondern auf Wahrscheinlichkeiten basiert. Das Atom ist eine probabilistische Einheit, die statistischen Gesetzen unterliegt und deren messbare Eigenschaften (Energie, Position, Geschwindigkeit usw.) nur dann zum Vorschein kommen, wenn eine Beobachtungsinteraktion stattfindet (ein Messvorgang).

Das Heisenberg-Atom erscheint als dichter Kern, der ausschließlich aus Protonen besteht (identifiziert 1919), umgeben von diffusen Wolken, die die Wahrscheinlichkeit der Anwesenheit von Elektronen darstellen. Diese Wolken können je nach Orbital unterschiedliche Formen annehmen.

Die Stabilität des Atoms blieb jedoch problematisch, ohne dass es eine klare Erklärung für die Neutralisierung elektrostatischer Abstoßungen gab.

Quantenzustände und Übergänge im Heisenberg-Atom

Elektronenbewegungen werden abstrakt und mathematisch durch Zustandsvektoren und Matrixoperatoren beschrieben. Elektronen haben keine wohldefinierten klassischen Flugbahnen, sondern existieren in überlagerten Quantenzuständen.

Die Übergänge zwischen diesen Zuständen sind quantifiziert und probabilistisch. Heisenbergs Unschärferelation spielt bei dieser Beschreibung eine grundlegende Rolle, da sie die Genauigkeit einschränkt, mit der die Position und der Impuls von Elektronen gleichzeitig ermittelt werden können.

Natur des Atoms von Erwin Schrödinger

Im Jahr 1926, die Gleichung vonErwin Schrödinger(1887-1961) ermöglichte die Beschreibung der Quantenzustände von Elektronen und markierte damit einen großen Fortschritt in der Quantenmechanik.

Das von Schrödinger vorgeschlagene Atommodell, bekannt alsWellenmechanikist eine weitere grundlegende Formulierung der Quantenmechanik. Schrödinger führte die nach ihm benannte Gleichung ein, um das Verhalten von Quantenteilchen wie Elektronen in einem Atom zu beschreiben. Mit seiner Gleichung kann Schrödinger die Schwingung dieser Welle und damit das von ihr ausgesandte Licht genau berechnen und findet das richtige Spektrum wie in Heisenbergs Theorie.

Im Schrödinger-Modell wird der Zustand eines Elektrons durch eine Wellenfunktion (Ψ) beschrieben, die alle möglichen Informationen über den Quantenzustand des Elektrons enthält.

Die Wellenfunktion ist nicht direkt beobachtbar, aber ihr Quadrat gibt die Wahrscheinlichkeitsdichte an, das Elektron an einer bestimmten Position im Raum zu finden. Das bedeutet, dass das Elektron keinen definierten Ort hat, sondern eine Wahrscheinlichkeitsverteilung seiner Anwesenheit.

Diese Wahrscheinlichkeitsbereiche werden aufgerufenAtomorbitale. Es istMax Born(1882-1970), der 1926 die probabilistische Interpretation der Wellenfunktion vorschlug. Diese Interpretation ermöglichte es, Atomorbitale als Regionen des Raumes zu verstehen, in denen die Wahrscheinlichkeit, ein Elektron zu finden, hoch ist.

Wellenfunktionen und Atomorbitale im Schrödinger-Atom

Die „Bewegungen“ von Elektronen werden durch Wellenfunktionen beschrieben, die Wahrscheinlichkeitsverteilungen der Anwesenheit in Atomorbitalen darstellen.

Elektronen haben keine wohldefinierten klassischen Flugbahnen, sondern existieren in überlagerten Quantenzuständen. Übergänge zwischen Energieniveaus werden durch Änderungen in der Wellenfunktion beschrieben, und die zeitliche Entwicklung der Wellenfunktion ist kontinuierlich und deterministisch. Es beschreibt eher Wahrscheinlichkeiten als klassische Bewegungen.

Natur des Atoms von Max Born

Im Jahr 1926Max Borns probabilistische Interpretation ermöglichte es, Atomorbitale als Wahrscheinlichkeitsbereiche zu verstehen.

Max Born interpretierte die Wellenfunktion ψ (Lösung der Schrödinger-Gleichung) nicht als materielle oder physikalische Welle, sondern als Wahrscheinlichkeitsamplitude. Insbesondere schlug er vor, dass die Wahrscheinlichkeitsdichte der Anwesenheit eines Teilchens (z. B. eines Elektrons) an einer bestimmten Position proportional zum quadrierten Absolutwert der Wellenfunktion ist.

Das Atom stellt nach Max Born einen völligen Bruch mit klassischen Vorstellungen dar: Es wird zu einer Einheit, bei der die Vorstellungen von Flugbahn, präziser Position und Determinismus zugunsten einer statistischen und probabilistischen Beschreibung auf der Grundlage von Wellenfunktionen aufgegeben werden. Diese Vision stellt eine der grundlegenden Grundlagen der Natur des modernen Atoms dar.

Wahrscheinlichkeitswolken und Quantenindeterminismus im Atom von Max Born

Im Atom nach Max Born folgen die Elektronen nicht den klassischen Bahnen wie in den Modellen von Rutherford oder Bohr. Ihre genaue Position zu einem bestimmten Zeitpunkt ist grundsätzlich unbestimmt. Anstelle präziser Flugbahnen sprechen wir von Wahrscheinlichkeitswolken, bei denen die Dichte der Wolke die Wahrscheinlichkeit der Anwesenheit des Elektrons darstellt.

Born zeigt, dass Elektronen keinen kontinuierlichen und deterministischen Bahnen folgen. Dieses Verhalten steht in direktem Zusammenhang mit dem durch Heisenbergs Unschärferelation eingeführten Quantenindeterminismus.

Natur des modernen Atoms

Die moderne Sicht auf das Atom beinhaltet fortgeschrittene Konzepte wie Spin, Spin-Bahn-Wechselwirkungen und relativistische Effekte.

Die Natur des modernen Atoms wird durch die Quantenmechanik beschrieben, die eine viel komplexere und differenziertere Sichtweise bietet als halbklassische Modelle wie die von Rutherford, Bohr, Heisenberg oder Schrödinger.

Die moderne Sichtweise umfasst Elektronenspin- und Spin-Bahn-Wechselwirkungen sowie die Quantenfeldtheorie zur Beschreibung von Wechselwirkungen zwischen Teilchen und Feldern, einschließlich relativistischer Effekte und elektromagnetischer Wechselwirkungen. QFT ist für das Verständnis hochenergetischer Phänomene und grundlegender Wechselwirkungen von wesentlicher Bedeutung.

Darüber hinaus beinhaltet es das Pauli-Ausschlussprinzip, das besagt, dass zwei Elektronen im selben Atom nicht den gleichen Satz von Quantenzahlen haben können. Dies erklärt den Schichtaufbau der Atome und die Periodizität der Elemente im Periodensystem.

Komplexe Wechselwirkungen und relativistische Effekte im modernen Atom

Im modernen Atom unterscheidet sich das Konzept der „Bewegung“ von Elektronen tatsächlich stark von dem klassischer Modelle. Anstatt über wohldefinierte Trajektorien zu sprechen, sprechen wir über Wahrscheinlichkeitsverteilungen und Quantenzustände.

Abschluss

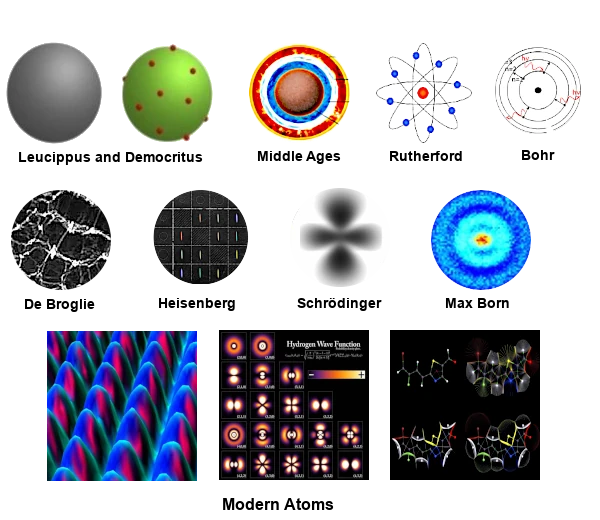
Das moderne Atom kann aufgrund seiner probabilistischen und nichtlokalen Natur nicht klassisch abgebildet werden. Allerdings können symbolische und schematische Darstellungen dabei helfen, bestimmte Aspekte des Atoms sichtbar zu machen. Atomorbitale, Wahrscheinlichkeitswolken und Energieniveaus können ein vollständigeres Bild des modernen Atoms vermitteln.

Hinweis: :
Der Begriff „nichtlokal“ bezieht sich im Kontext der Quantenmechanik und des modernen Atoms auf ein Phänomen, bei dem die Eigenschaften eines Teilchens durch Ereignisse in beliebiger Entfernung augenblicklich beeinflusst werden können, ohne dass es zu einer Informationsübertragung auf klassischem Wege kommt.