Fusion und Spaltung: Zwei Kernreaktionen, zwei Energiepfade

Kernreaktionen: Spaltung vs. Fusion

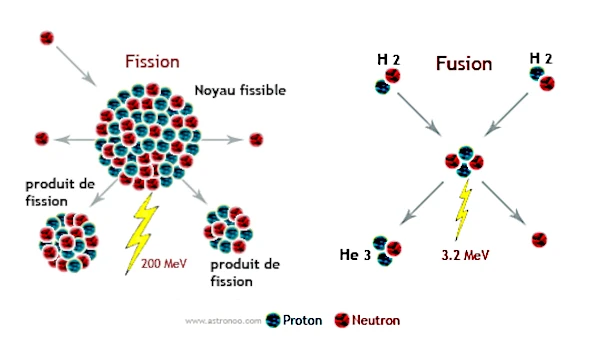
Kernreaktionen (Umwandlungen von Atomkernen) stellen die energiereichsten Prozesse im Universum dar. Es gibt zwei Hauptwege, um diese in der Materie enthaltene Energie freizusetzen: dieFission (prozess, bei dem sich ein schwerer Atomkern in zwei leichtere Kerne spaltet)und dieFusion (prozess, bei dem sich zwei leichte Atomkerne zu einem schwereren Kern vereinigen). Obwohl sich diese beiden Reaktionen im Prinzip grundlegend unterscheiden, gehorchen sie der berühmten Gleichung vonAlbert Einstein(1879-1955): \(E = mc^2\), der die Äquivalenz zwischen Masse und Energie herstellt.

Kernspaltung: Teilen, um zu existieren

Bei der Spaltung wird ein schwerer Kern (z. B. Uran-235 oder Plutonium-239) unter dem Einfluss eines Neutrons in zwei leichtere Fragmente zerlegt. Die freigesetzte Energie ergibt sich aus der Massendifferenz bezogen auf die Bindungsenergien pro Nukleon. Typischerweise setzt eine Spaltung von \(^{235}\)U ungefähr \(200\ \text{MeV}\) pro einzelner Kernspaltungsreaktion frei, nachdem ein Neutron eingefangen wurde.

Diese 1938 von Otto Hahn (1879-1968) und Fritz Strassmann (1902-1980) entdeckte und von Lise Meitner (1878-1968) und Otto Frisch (1904-1979) interpretierte Reaktion setzt beträchtliche Energie sowie mehrere Neutronen frei, die wiederum neue Spaltungen und damit eine Kettenreaktion auslösen können.

Die freigesetzte Energie stammt aus dem Massendefekt: Die Summe der Massen der Spaltprodukte ist kleiner als die Masse des ursprünglichen Kerns. Obwohl dieser Massendefekt winzig ist, wandelt er sich gemäß \(E = \Delta m c^2\) in kolossale Energie um, wobei \(\Delta m\) die Massendifferenz und \(c\) die Lichtgeschwindigkeit ist.

Zusammenfassend lässt sich sagen, dass sich der Kern teilt, weil es ab einer bestimmten Größe energetisch günstiger ist, in Form von zwei mittleren Kernen zu existieren als in der Form eines einzelnen instabilen schweren Kerns. Die Spaltung ist Ausdruck dieser Suche nach Stabilität, ausgelöst durch die Zugabe eines Neutrons.

Kernfusion: Einheit macht Stärke

Im Gegensatz dazu beinhaltet die Kernfusion die Vereinigung zweier leichter Atomkerne, etwa der Wasserstoffisotope (Deuterium \(^{2}\)H und Tritium \(^{3}\)H), zu einem schwereren Kern (Helium \(^{4}\)He). Dieser Prozess, der Sterne wie unsere Sonne antreibt, setzt pro Nukleon noch mehr Energie frei als die Kernspaltung. Um die elektrostatische Abstoßung zwischen positiv geladenen Kernen (Coulomb-Barriere) zu überwinden, sind extreme Temperaturbedingungen (in der Größenordnung von Millionen Grad) und Druck erforderlich. Die durch die D-T-Reaktion freigesetzte Energie liegt in der Größenordnung von \(17,6\ \text{MeV}\).

Die Beherrschung der Kernfusion auf der Erde stellt eine monumentale technologische Herausforderung dar, aber ihr Potenzial ist immens: reichlich Brennstoff, geringe Produktion langlebiger radioaktiver Abfälle und kein Risiko einer beschleunigten Reaktion.

Notiz:Wenn wir sagen, dass die D-T-Fusion freisetzt17,6 MeV, das ist Energieinsgesamt pro Elementarreaktion, also für die Wechselwirkung zwischen einem Deuteriumkern (\(^{2}\)H) und einem Tritiumkern (\(^{3}\)H). Diese Energie verteilt sich auf einen Helium-4-Kern (≈ 3,5 MeV) und ein Neutron (≈ 14,1 MeV). Da die Reaktion beinhaltet5 Baryonen(2+3), die an jedes Nukleon zurückgegebene Energie ist: \( \frac{17,6}{5} \ungefähr 3,5\ \text{MeV pro Baryon}. \) Es ist dieser Wert, den wir oft mit anderen Kernprozessen vergleichen: Die Spaltung setzt ≈ 0,9 MeV/Baryon frei, während die Fusion mehrere MeV/Baryon erreicht, was ihr höheres Energiepotential auf der reaktiven Massenskala verleiht.

Vergleich der beiden Energiepfade

Die folgende Tabelle fasst die Hauptmerkmale dieser beiden Kernreaktionen zusammen und hebt ihre grundlegenden Unterschiede hervor.

• Referenzen:Internationale Atomenergiebehörde (IAEA) (neues Fenster), ITER (neues Fenster).