Erste Messung des Abstands Erde-Sonne

Beschreibung des Bildes: Cassini-Messungen ermöglichten die Messung des Winkels α. Zwei Beobachter platzieren sich an zwei ausreichend weit entfernten Punkten auf der Erde (z. B. Paris und Cayenne) und notieren die Konfiguration der Sterne, die den beobachteten Stern umgeben. Sie können so die Winkel von den Beobachtungspunkten aus messen und daraus die Parallaxe α (im Bogenmaß) und dann den Abstand zwischen Erde und Mars ableiten.

Relative Größe des Sonnensystems

Zu Beginn des 17. Jahrhunderts hatten Wissenschaftler keine Ahnung von den Ausmaßen des Sonnensystems.

Dank der Gesetze vonJohannes Kepler(1571–1630) kennen wir die relativen Abstände der fünf damaligen Planeten im Verhältnis zur Sonne. Mit anderen Worten: Wir kennen die Entfernungen in einer unbekannten Einheit, der Erde-Sonne-Entfernung, aber wir kennen nicht die Erde-Sonne-Entfernung in km.

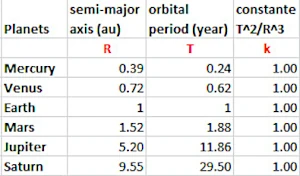
Das 1618 formulierte 3. Gesetz von Johannes Kepler zeigt den Zusammenhang zwischen der großen Halbachse der Umlaufbahn eines Planeten und seiner Rotationsperiode um die Sonne (Tabelle gegenüber). Der Würfel der großen Halbachse ist gleich dem Quadrat der Rotationsperiode (T2 / R3 = k), was die Umlaufbahn von Merkur auf 0,39 AE (eine viel später im Jahr 1958 geschaffene astronomische Einheit) und die des Saturn auf 9,55 astronomische Einheiten von der Sonne aus positioniert.

Die Messung einer einzelnen Entfernung (Planet-Sonne) wird den Maßstab des gesamten Systems und damit die von den Astronomen erwartete Entfernung Erde-Sonne in Kilometern liefern. Im Jahr 1687 entdeckte Isaac Newton das Gravitationsgesetz, das es ihm ermöglichte, die drei Keplerschen Gesetze zu erklären.

Hinweis: DieKeplers erstes GesetzDas „Gesetz der Umlaufbahnen“ (veröffentlicht 1609 in Astronomia nova) besagt, dass alle Körper in der Umlaufbahn elliptische Bahnen beschreiben, in deren Mittelpunkt die Sonne steht.
DortKeplers zweites GesetzDas „Flächengesetz“ (veröffentlicht 1609 in Astronomia nova) besagt, dass gleiche Flächen in gleichen Zeiten überstrichen werden.
DortKeplers drittes Gesetz„Das Gesetz der Perioden“ (veröffentlicht 1619 in Harmonices Mundi) besagt, dass das Quadrat der Sternperiode eines Planeten (Zeit zwischen zwei aufeinanderfolgenden Vorbeizügen vor einem Stern) direkt proportional zur dritten Potenz der großen Halbachse der elliptischen Flugbahn des Planeten ist.

Bildbeschreibung: T²/R³= k. Der theoretische Ausdruck von k wird 1687 dank der von Isaac Newton (1643–1727) formulierten Gleichungen der universellen Gravitation bekannt sein.

Messung der Entfernung Erde-Mars

So paradox es auch erscheinen mag, durch die Messung des Abstands Erde-Mars konnten Astronomen und Mathematiker des 17. Jahrhunderts eine Vorstellung von den Dimensionen des Sonnensystems gewinnen. Zu dieser Zeit bestand die Beobachtung hauptsächlich aus der Messung der Winkel von Himmelsobjekten, die von der Erde aus gesehen wurden. Dann sind es die trigonometrischen Berechnungen, die die Abstände ergeben.

Wie wurde erstmals die Entfernung Erde-Mars berechnet?

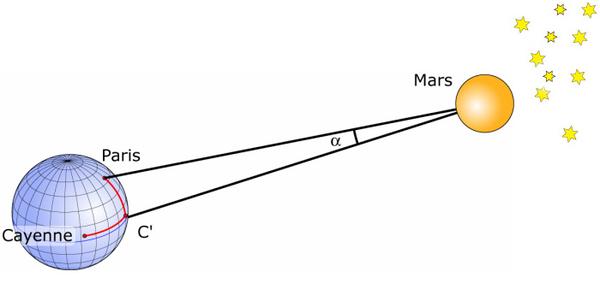
Im September 1672 maßen Jean-Dominique Cassini (1625–1712), Jean Picard, bekannt als Abbé Picard (1620–1682), und Jean Richer (1630–1696) die horizontale Parallaxe des Mars, als dieser Planet der Erde am nächsten kam (der Mars befand sich damals, von der Erde aus gesehen, gegenüber der Sonne). Um diese Messung durchzuführen, ist es notwendig, die Positionen des Mars im Verhältnis zu viel weiter entfernten Sternen von zwei sehr weit entfernten Punkten aus zu beobachten.

Cassini aus Paris und Richer aus Cayenne messen die Parallaxe des Mars. Diese Messung bezogen auf die Basis, die durch den Äquatorradius der Erde gebildet wird, ergibt eine horizontale Parallaxe von p=24" ⇒ Erde-Mars = 54.746.000 km. Um die Parallaxe des Mars aus Beobachtungen von Paris und Cayenne aus zu bestimmen, ist es notwendig, den Unterschied zwischen den Breitengraden und den Unterschied zwischen den Längengraden von Paris und Cayenne mit höchster Präzision zu kennen.

Der Breitengrad ist leicht zu messen, der Längengrad ist jedoch zu diesem Zeitpunkt viel schwieriger.

Cassini gibt jedoch an, dass er den Längengrad mit mehreren Methoden gemessen hat, um einen Durchschnitt zu erhalten:

• Die Beobachtung einer Sonnenfinsternis, deren verschiedene Phasen in astronomischen Sammlungen in Stunden des Pariser Meridians identifiziert werden.
• Beobachtung von Finsternissen der Galileischen Satelliten des Jupiter, die mehrmals täglich auftreten.
• Beobachtung der Meridianhöhen der Sonne.

Alles in allem ergibt sich ein Durchschnitt von 3 Stunden 39 Minuten ±10 Minuten. Richer und Cassini beobachteten daher im September 1672 den Planeten Mars. Mars wird nahe an einem Stern im Wassermann (Ψ Aquarii) vorbeiziehen. Auf dem Bild entspricht Punkt C' dem Breitengrad von C (Cayenne) und dem Längengrad von P (Paris). Cassini nutzt zwei gleichzeitige Beobachtungen des Mars, eine von P, die andere von C‘. Der Paris-Cayenne-Winkel vom Mars beträgt den Winkel α=14". Aber die Parallaxe des Mars ist der Winkel, in dem Mars den Radius der Erde sieht. Die Berechnung der Proportionalität zwischen dem Paris-Cayenne-Winkel und der Parallaxe des Mars ergibt 24" ± 5"

Sobald die Parallaxe des Mars bekannt ist, können wir mithilfe der Trigonometrie den Abstand Erde-Mars (D) als Funktion des Radius (R) der Erde ermitteln:
D = R×3600/24×180/π oder 8600 R
D = 8600 * 6371 = 54.790.600 km

Hinweis: Der Breitengrad ist die Nord- oder Südposition eines Punktes auf der Erde, mit anderen Worten der Winkel mit der Äquatorialebene (von 0° am Äquator bis 90° am Nordpol und -90° am Südpol).

Hinweis: Der Längengrad ist die Ost-West-Position eines Punktes auf der Erde, die einem Zeitunterschied zur Ebene des Greenwich-Meridians (Ursprungsmeridian, Längengrad 0°) entspricht. Dieser Versatz variiert von +180° Richtung Westen bis -180° Richtung Osten.

Berechnung des Abstands Erde-Sonne

Sobald der Abstand Erde-Mars bekannt war, konnte der Abstand Erde-Sonne mithilfe des dritten Keplerschen Gesetzes berechnet werden.

Cassini wusste, dass sich der Mars bei 0,38 au = 3/8 au befand. Erde-Sonne = 8/3 x 8600 R = 23000 R ±5000 Erdradien. Cassini gibt uns den Wert des Erdradius in Meilen an: R = 1500 Meilen.

Damals gab es je nach Region eine Vielzahl unterschiedlicher Definitionen der Liga. Angenommen, der Erdradius wird in Abbé-Picard-Ligen angegeben, was ab 1671 3707 Metern entspricht. R = 1500 x 3,707 = 5560,5 km von wo: Erde-Sonne = 127.891.500 km bei ±27.802.500 km

Dieses bemerkenswerte Ergebnis stellt die erste Messung des Abstands Erde-Sonne dar. Dank des dritten Keplerschen Gesetzes ergibt sich dieser Abstanddas Ausmaß des gesamten Sonnensystems T2/R3=k.

Berechnung der Entfernungen von den Umlaufbahnen der Erde und des Mars

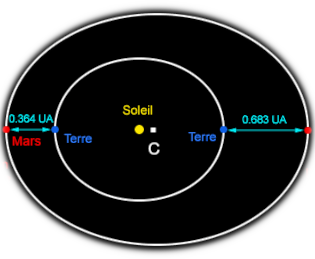
C = Mittelpunkt der Ellipse, die die Umlaufbahn des Mars darstellt
CM_Marsch= Große Halbachse der Umlaufbahn des Mars
Exzentrizität der Marsbahn = CS_Sonne / CM_Marsch= 0,093
CM_Marsch = CS_Sonne+S_SonneT_Erde + T_ErdeM_Marsch
CM_Marsch=T_ErdeM_Marsch+S_SonneT_Erde / 1-CS_Sonne
T_ErdeM_Marsch= 54.790.600 km
P.T._Erde(Erdperiode) = 1 Jahr (365 Tage)
PN_Marsch(Marsperiode) = 1,88 Jahre (686 Tage)
T_ErdeS_Sonne=T_ErdeM_Marsch / 1-CS_Sonne(PM_Marsch/PT_Erde)2/3 -1
1-CS_Sonne(PM_Marsch/PT_Erde)2/3 -1 = 0,38 oder 3/8 ⇒ T_ErdeS_Sonne= 54.790.600 x 8/3 = 150.000.000 km