Première mesure de la distance Terre-Soleil

Description de l'image : Les mesures de Cassini ont permis de mesurer l’angle α. Deux observateurs se placent en deux points de la Terre suffisamment éloignés (Paris et Cayenne par exemple) et notent la configuration des étoiles entourant l’astre observé. Ils peuvent ainsi mesurer les angles depuis les points d'observation puis en déduire la parallaxe α (en radians) puis la distance Terre-Mars.

Taille relative du système solaire

Au début du 17ème siècle, les scientifiques n'ont aucune idée des dimensions du système solaire.

Grâce aux lois de Johannes Kepler (1571−1630) on connait les distances relatives des cinq planètes de l'époque par rapport au Soleil. En d'autres termes, on connait les distances dans une unité inconnue, la distance Terre-Soleil mais on ne connait pas la distance Terre-Soleil en km.

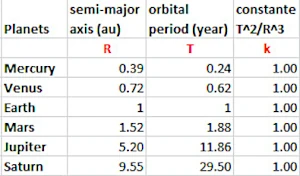
La 3ème loi de Johannes Kepler formulée en 1618 montre la relation entre le demi-grand axe de l'orbite d'une planète et sa période de rotation autour du Soleil (tableau ci-contre). Le cube du demi-grand axe est égal au carré de la période de rotation (T2 / R3 = k) ce qui positionne l'orbite de Mercure à 0.39 ua (unité astronomique créée beaucoup plus tard en 1958) et celle de Saturne à 9.55 unités astronomiques du Soleil.

La mesure d'une seule distance (planète-Soleil) va donner l'échelle de tout le système et donc la distance Terre-Soleil en km tant attendue par les astronomes. En 1687, Isaac Newton découvre la loi de la gravitation qui lui permet d'expliquer les trois lois de Kepler.

N. B. : La première loi de Kepler « loi des orbites » (publiée en 1609 dans Astronomia nova), stipule que tous les corps en orbite décrivent des trajectoires elliptiques, dont le Soleil occupe l'un des foyers.
La deuxième loi de Kepler « loi des aires » (publiée en 1609 dans Astronomia nova), stipule que des aires égales sont balayées dans des temps égaux.
La troisième loi de Kepler « la loi des périodes » (publiée en 1619 dans Harmonices Mundi), stipule que le carré de la période sidérale d'une planète (temps entre deux passages successifs devant une étoile) est directement proportionnel au cube du demi-grand axe de la trajectoire elliptique de la planète.

Description de l'image : T² / R³ = k. L'expression théorique de k sera connue en 1687 grâce aux équations de la gravitation universelle formulées par Isaac Newton (1643−1727).

Mesure de la distance Terre-Mars

Aussi paradoxal que cela puisse paraitre, c'est par la mesure de la distance Terre-Mars que les astronomes et mathématiciens du 17ème siècle ont pu se faire une idée des dimensions du système solaire. A cette époque, l'observation se résume principalement par la mesure des angles des objets célestes vus de la Terre. Ensuite ce sont les calculs de trigonométrie qui donnent les distances.

Comment a été calculée la distance Terre-Mars pour la première fois ?

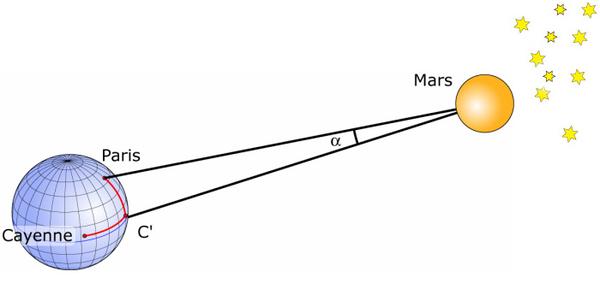
En septembre 1672, Jean-Dominique Cassini (1625−1712), Jean Picard dit l'abbé Picard (1620−1682) et Jean Richer (1630−1696) mesurent la parallaxe horizontale de Mars quand cette planète passait au plus près de la Terre (Mars se trouve alors, vu de la Terre, à l'opposé du Soleil). Pour réaliser cette mesure, il faut observer les positions de Mars par rapport aux étoiles beaucoup plus lointaines depuis deux points très distants.

Cassini depuis Paris et Richer depuis Cayenne mesure la parallaxe de Mars. Cette mesure rapportée à la base formée par le rayon équatorial de la Terre donne une parallaxe horizontale de p=24" ⇒ Terre-Mars = 54 746 000 km. Pour déterminer la parallaxe de Mars à partir des observations faites depuis Paris et Cayenne, il est nécessaire de connaitre avec un maximum de précision l'écart entre les latitudes et l'écart entre les longitudes de Paris et Cayenne.

La latitude est facile à mesurer mais la longitude est beaucoup plus difficile, à l'époque.

Cassini précise cependant qu’il a mesuré la longitude par plusieurs méthodes pour obtenir une moyenne :

• L'observation d'une éclipse dont les différentes phases sont repérées en heures du méridien de Paris, dans les recueils astronomiques.
• L'observation des éclipses des satellites Galiléens de Jupiter qui se produisent plusieurs fois par jour.
• L'observation des hauteurs méridiennes du Soleil.

L’ensemble donne une moyenne de 3 h 39 min ±10 min. Richer et Cassini observent donc la planète Mars pendant le mois de septembre 1672. Mars passera à proximité d’une étoile du Verseau (Ψ Aquarii). Sur l'image, le point C'correspond à la latitude de C (Cayenne) et à la longitude de P (Paris). Cassini utilise deux observations simultanées de Mars, l’une depuis P, l’autre depuis C’. L'angle Paris Cayenne depuis Mars est l’angle α=14". Mais la parallaxe de Mars est l'angle sous lequel Mars voit le rayon de la Terre. Le calcul de proportionnalité entre l’angle Paris Cayenne et la parallaxe de Mars donne 24" ± 5"

Une fois connue la parallaxe de Mars, la trigonométrie permet d'obtenir la distance Terre-Mars (D) en fonction du rayon (R) de la Terre :
D = R×3600/24×180/π soit 8600 R
D = 8600 * 6371 = 54 790 600 km

N. B. : La latitude est le positionnement nord ou sud d'un point sur Terre, en d'autres termes c'est l'angle avec le plan équatorial (de 0° à l'équateur à 90° au pôle nord et -90° au pôle sud).

N. B. : La longitude est le positionnement Est-Ouest d'un point sur Terre ce qui correspond à un décalage horaire avec le plan du méridien de Greenwich (méridien origine, de longitude 0°). Ce décalage varie de +180° vers l'ouest à -180° vers l'est).

Calcul de la distance Terre-Soleil

Dès que la distance Terre-Mars fût connue, la distance Terre-Soleil pu être calculée grâce à la troisième loi de Kepler.

Cassini savait que Mars était à 0.38 ua = 3/8 ua. Terre-Soleil = 8/3 x 8600 R = 23000 R ±5000 rayons terrestres. Cassini nous donne la valeur du rayon terrestre en lieues : R = 1500 lieues.

A l’époque il y a un grand nombre de définitions de la lieue suivant les régions. Supposons que le rayon terrestre soit donné en lieue de l'abbé Picard qui à partir de 1671 est égal à 3707 mètres. R = 1500 x 3,707 = 5560.5 km d'où : Terre-Soleil = 127 891 500 km à ±27 802 500 km

Ce résultat remarquable constitue la première mesure de la distance Terre-Soleil. Grâce à la troisième loi de Kepler, cette distance va donner l'échelle de tout le système solaire T2/R3=k.

Calcul des distances à partir des orbites de la Terre et de Mars

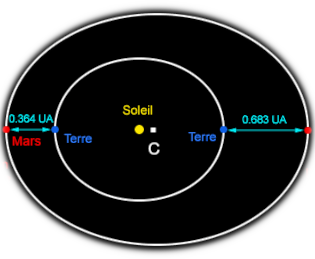
C = Centre de l'ellipse représentant l'orbite de Mars
CM_mars = Demi-grand axe de l'orbite de Mars
Excentricité de l'orbite de Mars = CS_soleil / CM_mars = 0.093
CM_mars = CS_soleil + S_soleilT_terre + T_terreM_mars
CM_mars = T_terreM_mars + S_soleilT_terre / 1-CS_soleil
T_terreM_mars = 54 790 600 km
PT_terre (période de la Terre) = 1 an (365 jours)
PM_mars (période de Mars) = 1,88 an (686 jours)
T_terreS_soleil = T_terreM_mars / 1-CS_soleil(PM_mars/PT_terre)2/3 -1
1-CS_soleil(PM_mars/PT_terre)2/3 -1 = 0.38 soit 3/8 ⇒ T_terreS_soleil = 54 790 600 x 8/3 = 150 000 000 km