First Measurement of the Earth-Sun Distance

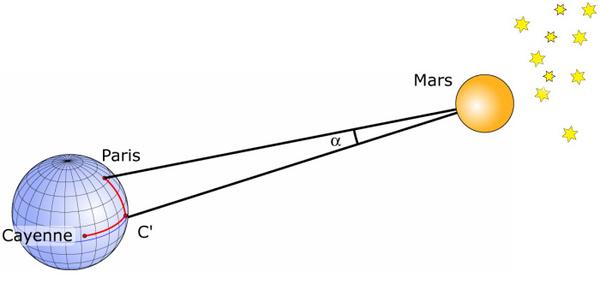
Image description: Cassini's measurements allowed the angle α to be measured. Two observers position themselves at two sufficiently distant points on Earth (Paris and Cayenne, for example) and note the configuration of the stars surrounding the observed celestial body. They can thus measure the angles from the observation points and then deduce the parallax α (in radians) and then the Earth-Mars distance.

Relative Size of the Solar System

At the beginning of the 17th century, scientists had no idea of the dimensions of the solar system.

Thanks to the laws of Johannes Kepler (1571−1630), we know the relative distances of the five planets of the time with respect to the Sun. In other words, we know the distances in an unknown unit, the Earth-Sun distance, but we do not know the Earth-Sun distance in km.

The 3rd law of Johannes Kepler formulated in 1618 shows the relationship between the semi-major axis of a planet's orbit and its period of rotation around the Sun (table on the right). The cube of the semi-major axis is equal to the square of the period of rotation (T2 / R3 = k), which positions Mercury's orbit at 0.39 au (astronomical unit created much later in 1958) and Saturn's at 9.55 astronomical units from the Sun.

The measurement of a single distance (planet-Sun) will give the scale of the entire system and thus the long-awaited Earth-Sun distance in km by astronomers. In 1687, Isaac Newton discovered the law of gravitation, which allowed him to explain Kepler's three laws.

N. B. : The first law of Kepler "law of orbits" (published in 1609 in Astronomia nova), stipulates that all bodies in orbit describe elliptical trajectories, one of whose foci is occupied by the Sun.
The second law of Kepler "law of areas" (published in 1609 in Astronomia nova), stipulates that equal areas are swept in equal times.
The third law of Kepler "law of periods" (published in 1619 in Harmonices Mundi), stipulates that the square of the sidereal period of a planet (time between two successive passages in front of a star) is directly proportional to the cube of the semi-major axis of the planet's elliptical trajectory.

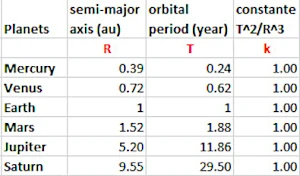
Image description: T² / R³ = k. The theoretical expression of k will be known in 1687 thanks to the equations of universal gravitation formulated by Isaac Newton (1643−1727).

Measurement of the Earth-Mars Distance

As paradoxical as it may seem, it was by measuring the Earth-Mars distance that the astronomers and mathematicians of the 17th century were able to get an idea of the dimensions of the solar system. At that time, observation mainly consisted of measuring the angles of celestial objects seen from Earth. Then trigonometric calculations give the distances.

How was the Earth-Mars distance calculated for the first time?

In September 1672, Jean-Dominique Cassini (1625−1712), Jean Picard, known as Abbé Picard (1620−1682), and Jean Richer (1630−1696) measured the horizontal parallax of Mars when this planet was closest to Earth (Mars is then, seen from Earth, opposite the Sun). To make this measurement, it is necessary to observe the positions of Mars relative to the much more distant stars from two very distant points.

Cassini from Paris and Richer from Cayenne measure the parallax of Mars. This measurement related to the base formed by the equatorial radius of the Earth gives a horizontal parallax of p=24" ⇒ Earth-Mars = 54,746,000 km. To determine the parallax of Mars from the observations made from Paris and Cayenne, it is necessary to know with maximum precision the difference between the latitudes and the difference between the longitudes of Paris and Cayenne.

Latitude is easy to measure, but longitude is much more difficult at the time.

Cassini specifies, however, that he measured the longitude by several methods to obtain an average:

• The observation of an eclipse whose different phases are noted in hours of the Paris meridian, in the astronomical records.
• The observation of the eclipses of the Galilean satellites of Jupiter, which occur several times a day.
• The observation of the meridian heights of the Sun.

The whole gives an average of 3 h 39 min ±10 min. Richer and Cassini therefore observe the planet Mars during the month of September 1672. Mars will pass near a star in Aquarius (Ψ Aquarii). In the image, point C' corresponds to the latitude of C (Cayenne) and to the longitude of P (Paris). Cassini uses two simultaneous observations of Mars, one from P, the other from C'. The angle Paris Cayenne from Mars is the angle α=14". But the parallax of Mars is the angle under which Mars sees the radius of the Earth. The proportionality calculation between the Paris Cayenne angle and the parallax of Mars gives 24" ± 5"

Once the parallax of Mars is known, trigonometry makes it possible to obtain the Earth-Mars distance (D) as a function of the radius (R) of the Earth:
D = R×3600/24×180/π or 8600 R
D = 8600 * 6371 = 54,790,600 km

N. B. : Latitude is the north or south positioning of a point on Earth, in other words, it is the angle with the equatorial plane (from 0° at the equator to 90° at the north pole and -90° at the south pole).

N. B. : Longitude is the East-West positioning of a point on Earth, which corresponds to a time difference with the plane of the Greenwich meridian (origin meridian, longitude 0°). This difference varies from +180° to the west to -180° to the east).

Calculation of the Earth-Sun Distance

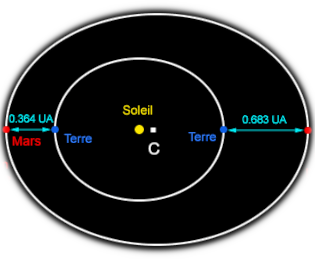
As soon as the Earth-Mars distance was known, the Earth-Sun distance could be calculated thanks to Kepler's third law.

Cassini knew that Mars was at 0.38 au = 3/8 au. Earth-Sun = 8/3 x 8600 R = 23000 R ±5000 terrestrial radii. Cassini gives us the value of the terrestrial radius in leagues: R = 1500 leagues.

At the time, there were a large number of definitions of the league depending on the regions. Suppose that the terrestrial radius is given in the league of Abbé Picard which from 1671 is equal to 3707 meters. R = 1500 x 3.707 = 5560.5 km hence: Earth-Sun = 127,891,500 km at ±27,802,500 km

This remarkable result constitutes the first measurement of the Earth-Sun distance. Thanks to Kepler's third law, this distance will give the scale of the entire solar system T2/R3=k.

Calculation of Distances from the Orbits of Earth and Mars

C = Center of the ellipse representing Mars' orbit
CM_mars = Semi-major axis of Mars' orbit
Eccentricity of Mars' orbit = CS_sun / CM_mars = 0.093
CM_mars = CS_sun + S_sunE_earth + E_earthM_mars
CM_mars = E_earthM_mars + S_sunE_earth / 1-CS_sun
E_earthM_mars = 54,790,600 km
PE_earth (period of Earth) = 1 year (365 days)
PM_mars (period of Mars) = 1.88 years (686 days)
E_earthS_sun = E_earthM_mars / 1-CS_sun(PM_mars/PE_earth)2/3 -1
1-CS_sun(PM_mars/PE_earth)2/3 -1 = 0.38 or 3/8 ⇒ E_earthS_sun = 54,790,600 x 8/3 = 150,000,000 km