Primera Medición de la Distancia Tierra-Sol

Descripción de la imagen: Las mediciones de Cassini permitieron medir el ángulo α. Dos observadores se colocan en dos puntos de la Tierra suficientemente alejados (París y Cayena, por ejemplo) y anotan la configuración de las estrellas que rodean el astro observado. Así pueden medir los ángulos desde los puntos de observación y luego deducir la paralaje α (en radianes) y luego la distancia Tierra-Marte.

Tamaño Relativo del Sistema Solar

A principios del siglo XVII, los científicos no tenían idea de las dimensiones del sistema solar.

Gracias a las leyes de Johannes Kepler (1571−1630) conocemos las distancias relativas de los cinco planetas de la época con respecto al Sol. En otras palabras, conocemos las distancias en una unidad desconocida, la distancia Tierra-Sol, pero no conocemos la distancia Tierra-Sol en km.

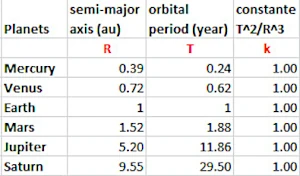
La 3ª ley de Johannes Kepler formulada en 1618 muestra la relación entre el semieje mayor de la órbita de un planeta y su período de rotación alrededor del Sol (tabla a la derecha). El cubo del semieje mayor es igual al cuadrado del período de rotación (T2 / R3 = k), lo que sitúa la órbita de Mercurio a 0.39 ua (unidad astronómica creada mucho más tarde en 1958) y la de Saturno a 9.55 unidades astronómicas del Sol.

La medición de una sola distancia (planeta-Sol) dará la escala de todo el sistema y, por lo tanto, la distancia Tierra-Sol en km tan esperada por los astrónomos. En 1687, Isaac Newton descubrió la ley de la gravitación, que le permitió explicar las tres leyes de Kepler.

N. B. : La primera ley de Kepler "ley de las órbitas" (publicada en 1609 en Astronomia nova), estipula que todos los cuerpos en órbita describen trayectorias elípticas, uno de cuyos focos está ocupado por el Sol.
La segunda ley de Kepler "ley de las áreas" (publicada en 1609 en Astronomia nova), estipula que áreas iguales se barren en tiempos iguales.
La tercera ley de Kepler "ley de los períodos" (publicada en 1619 en Harmonices Mundi), estipula que el cuadrado del período sideral de un planeta (tiempo entre dos pasos sucesivos frente a una estrella) es directamente proporcional al cubo del semieje mayor de la trayectoria elíptica del planeta.

Descripción de la imagen: T² / R³ = k. La expresión teórica de k se conocerá en 1687 gracias a las ecuaciones de la gravitación universal formuladas por Isaac Newton (1643−1727).

Medición de la Distancia Tierra-Marte

Tan paradójico como pueda parecer, fue midiendo la distancia Tierra-Marte que los astrónomos y matemáticos del siglo XVII pudieron hacerse una idea de las dimensiones del sistema solar. En esa época, la observación se resume principalmente en la medición de los ángulos de los objetos celestes vistos desde la Tierra. Luego, los cálculos de trigonometría dan las distancias.

¿Cómo se calculó la distancia Tierra-Marte por primera vez?

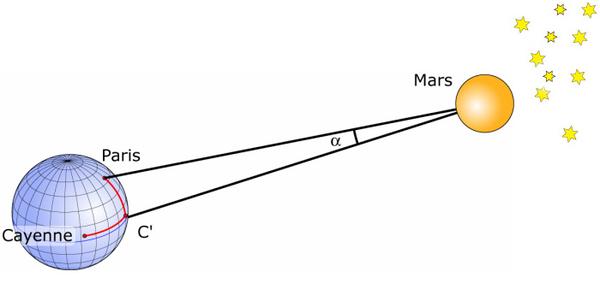
En septiembre de 1672, Jean-Dominique Cassini (1625−1712), Jean Picard, conocido como el abad Picard (1620−1682), y Jean Richer (1630−1696) midieron la paralaje horizontal de Marte cuando este planeta pasaba más cerca de la Tierra (Marte se encuentra entonces, visto desde la Tierra, opuesto al Sol). Para realizar esta medición, es necesario observar las posiciones de Marte en relación con las estrellas mucho más lejanas desde dos puntos muy distantes.

Cassini desde París y Richer desde Cayena miden la paralaje de Marte. Esta medición relacionada con la base formada por el radio ecuatorial de la Tierra da una paralaje horizontal de p=24" ⇒ Tierra-Marte = 54,746,000 km. Para determinar la paralaje de Marte a partir de las observaciones realizadas desde París y Cayena, es necesario conocer con la máxima precisión la diferencia entre las latitudes y la diferencia entre las longitudes de París y Cayena.

La latitud es fácil de medir, pero la longitud es mucho más difícil en esa época.

Cassini precisa, sin embargo, que midió la longitud por varios métodos para obtener un promedio:

• La observación de un eclipse cuyas diferentes fases se anotan en horas del meridiano de París, en los registros astronómicos.
• La observación de los eclipses de los satélites galileanos de Júpiter, que ocurren varias veces al día.
• La observación de las alturas meridianas del Sol.

El conjunto da un promedio de 3 h 39 min ±10 min. Richer y Cassini observan, por lo tanto, el planeta Marte durante el mes de septiembre de 1672. Marte pasará cerca de una estrella de Acuario (Ψ Aquarii). En la imagen, el punto C' corresponde a la latitud de C (Cayena) y a la longitud de P (París). Cassini utiliza dos observaciones simultáneas de Marte, una desde P, la otra desde C'. El ángulo París Cayena desde Marte es el ángulo α=14". Pero la paralaje de Marte es el ángulo bajo el cual Marte ve el radio de la Tierra. El cálculo de proporcionalidad entre el ángulo París Cayena y la paralaje de Marte da 24" ± 5"

Una vez conocida la paralaje de Marte, la trigonometría permite obtener la distancia Tierra-Marte (D) en función del radio (R) de la Tierra:
D = R×3600/24×180/π o 8600 R
D = 8600 * 6371 = 54,790,600 km

N. B. : La latitud es el posicionamiento norte o sur de un punto en la Tierra, en otras palabras, es el ángulo con el plano ecuatorial (de 0° en el ecuador a 90° en el polo norte y -90° en el polo sur).

N. B. : La longitud es el posicionamiento Este-Oeste de un punto en la Tierra, lo que corresponde a una diferencia horaria con el plano del meridiano de Greenwich (meridiano origen, de longitud 0°). Esta diferencia varía de +180° hacia el oeste a -180° hacia el este).

Cálculo de la Distancia Tierra-Sol

Tan pronto como se conoció la distancia Tierra-Marte, se pudo calcular la distancia Tierra-Sol gracias a la tercera ley de Kepler.

Cassini sabía que Marte estaba a 0.38 ua = 3/8 ua. Tierra-Sol = 8/3 x 8600 R = 23000 R ±5000 radios terrestres. Cassini nos da el valor del radio terrestre en leguas: R = 1500 leguas.

En esa época, había un gran número de definiciones de la legua según las regiones. Supongamos que el radio terrestre se da en la legua del abad Picard que a partir de 1671 es igual a 3707 metros. R = 1500 x 3.707 = 5560.5 km de ahí: Tierra-Sol = 127,891,500 km a ±27,802,500 km

Este resultado notable constituye la primera medición de la distancia Tierra-Sol. Gracias a la tercera ley de Kepler, esta distancia dará la escala de todo el sistema solar T2/R3=k.

Cálculo de Distancias a Partir de las Órbitas de la Tierra y Marte

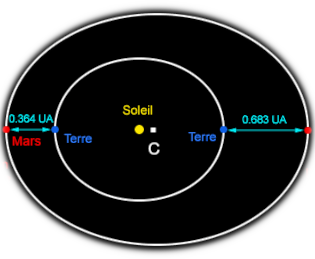
C = Centro de la elipse que representa la órbita de Marte
CM_marte = Semieje mayor de la órbita de Marte
Excentricidad de la órbita de Marte = CS_sol / CM_marte = 0.093
CM_marte = CS_sol + S_solT_tierra + T_tierraM_marte
CM_marte = T_tierraM_marte + S_solT_tierra / 1-CS_sol
T_tierraM_marte = 54,790,600 km
PT_tierra (período de la Tierra) = 1 año (365 días)
PM_marte (período de Marte) = 1.88 años (686 días)
T_tierraS_sol = T_tierraM_marte / 1-CS_sol(PM_marte/PT_tierra)2/3 -1
1-CS_sol(PM_marte/PT_tierra)2/3 -1 = 0.38 o 3/8 ⇒ T_tierraS_sol = 54,790,600 x 8/3 = 150,000,000 km