¿A qué distancia está el horizonte?

Comprender la distancia aparente del horizonte

El horizonte es el límite aparente entre la Tierra y el cielo. Su distancia depende de la curvatura terrestre, la altura del observador y la refracción atmosférica. Esta distancia se puede calcular mediante una fórmula geométrica simple sin tener en cuenta la refracción atmosférica.

Distancia geométrica simple al horizonte

La distancia al horizonte, en una Tierra ideal perfectamente esférica y sin atmósfera, se calcula mediante \(\,d = \sqrt{2Rh + h^2}\,\) donde \(R\) es el radio terrestre (\(\approx 6371\) km) y \(h\) la altura del observador. Por ejemplo, a 2 m de altura, el horizonte geométrico está a unos 5 km.

Cálculo detallado de la distancia al horizonte

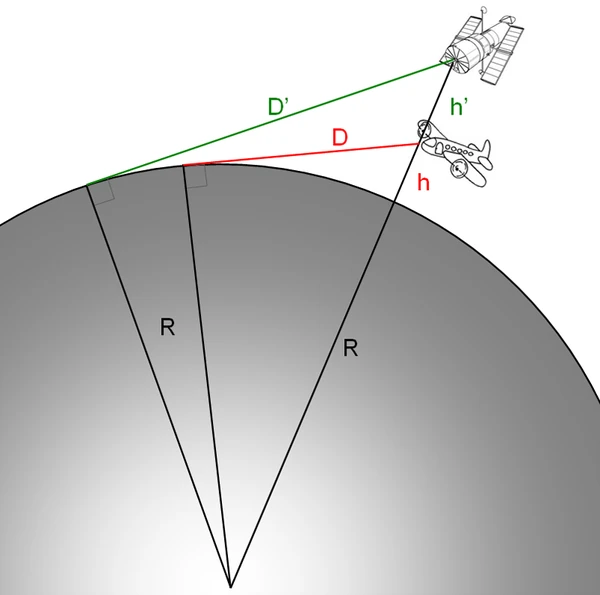
Consideremos un observador situado a una altura \(h\) sobre la superficie terrestre. Sea \(R\) el radio medio de la Tierra (\(R \approx 6371\) km). La línea que une el ojo del observador con el punto de tangencia en la superficie es perpendicular al radio terrestre en ese punto. El triángulo formado por el centro de la Tierra, el punto de tangencia y el observador es rectángulo. Aplicando el teorema de Pitágoras: \( (R + h)^2 = R^2 + d^2 \) donde \(d\) es la distancia en línea recta entre el observador y el horizonte. La distancia en el suelo, siguiendo la curvatura, es: \( s = R \cdot \theta \) con \(\theta = \arccos\left( \frac{R}{R+h} \right)\). Combinando: \( s = R \cdot \arccos\left( \frac{R}{R+h} \right) \) y para \(h \ll R\), obtenemos la aproximación: \( s \approx \sqrt{2Rh + h^2} \)

Cálculo de la distancia al horizonte con corrección atmosférica

En realidad, la refracción atmosférica aumenta ligeramente esta distancia porque los rayos de luz se curvan hacia el suelo. En condiciones estándar, este efecto se modela reemplazando \(R\) por \(R / (1 - k)\) donde \(k \approx 0{,}13\).

Tabla comparativa de distancias al horizonte según la altitud

N.B.: El horizonte terrestre nunca existe completamente a partir del momento en que se abandona la superficie: cuanto más se sube, más se agranda la porción visible de la Tierra. Desde la ISS (408 km), se vislumbra aproximadamente el 3,2% de la superficie total (≈9 millones de km²). En órbita geoestacionaria (36.000 km), se ve exactamente la mitad del planeta. Para observar el 99% de la superficie de un solo vistazo, habría que alcanzar unos 21.700 km de altitud. Más allá, el horizonte retrocede prácticamente hasta el borde opuesto de la Tierra, pero solo desaparece por completo a distancia infinita.