Wie weit ist der Horizont entfernt?

Die scheinbare Entfernung vom Horizont verstehen

Der Horizont ist die scheinbare Grenze zwischen Erde und Himmel. Seine Entfernung hängt von der Erdkrümmung, der Höhe des Beobachters und der atmosphärischen Brechung ab. Dieser Abstand kann mit einer einfachen geometrischen Formel berechnet werden, ohne die atmosphärische Brechung zu berücksichtigen.

Einfache geometrische Entfernung vom Horizont

Der Abstand zum Horizont wird auf einer idealen, perfekt kugelförmigen Erde ohne Atmosphäre durch \(\,d = \sqrt{2Rh + h^2}\,\) berechnet, wobei \(R\) der Erdradius (\(\ca. 6371\) km) und \(h\) die Höhe des Beobachters ist. In 2 m Höhe liegt der geometrische Horizont beispielsweise beica. 5 km.

Detaillierte Berechnung der Entfernung vom Horizont

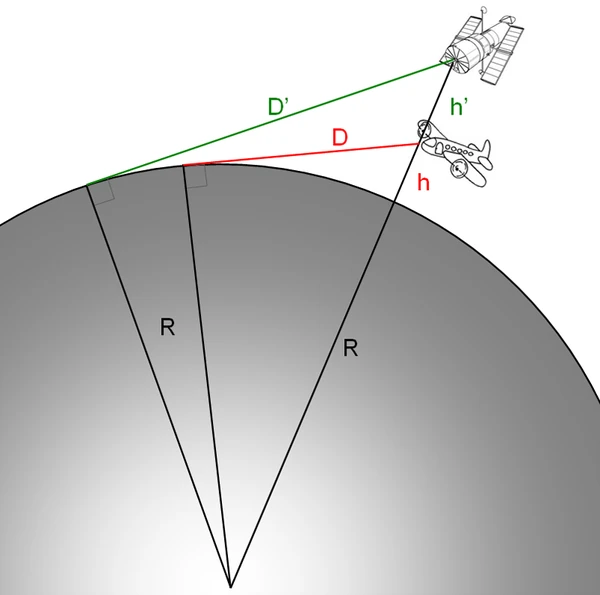
Stellen Sie sich einen Beobachter vor, der sich in einer Höhe \(h\) über der Erdoberfläche befindet. Sei \(R\) der durchschnittliche Radius der Erde (\(R \ca. 6371\) km). Die Linie, die das Auge des Beobachters mit dem Berührungspunkt an der Oberfläche verbindet, steht an diesem Punkt senkrecht zum Erdradius. Das Dreieck zwischen dem Erdmittelpunkt, dem Berührungspunkt und dem Beobachter ist rechtwinklig. Durch Anwendung des Satzes des Pythagoras: \( (R + h)^2 = R^2 + d^2 \) Dabei ist \(d\) der geradlinige Abstand zwischen dem Beobachter und dem Horizont. Der Abstand zum Boden, der Krümmung folgend, beträgt: \( s = R\cdot\theta \) mit \(\theta = \arccos\left( \frac{R}{R+h} \right)\). Durch die Kombination von: \( s = R \cdot \arccos\left( \frac{R}{R+h} \right) \) und für \(h \ll R\) erhalten wir die Näherung: \( s \ approx \sqrt{2Rh + h^2} \)

Berechnung der Horizontentfernung mit atmosphärischer Korrektur

In Wirklichkeit vergrößert die atmosphärische Brechung diesen Abstand geringfügig, da die Lichtstrahlen zum Boden hin gebogen werden. Unter Standardbedingungen modellieren wir diesen Effekt, indem wir \(R\) durch \(R / (1 - k)\) durch \(k \ungefähr 0{,}13\) ersetzen.

Vergleichstabelle der Entfernungen vom Horizont nach Höhe

Hinweis::
Der Erdhorizont existiert von dem Moment an, in dem wir die Erdoberfläche verlassen, nie vollständig: Je höher wir kommen, desto größer wird der sichtbare Teil der Erde. Von der ISS (408 km) aus können wir etwa 3,2 % der Gesamtoberfläche (≈9 Millionen km²) sehen. Im geostationären Orbit (36.000 km) sehen wir genau die Hälfte des Planeten. Um 99 % der Oberfläche auf einen Blick zu beobachten, müsste man eine Höhe von etwa 21.700 km erreichen. Darüber hinaus weicht der Horizont fast bis zum gegenüberliegenden Erdrand zurück, verschwindet aber erst in unendlicher Entfernung vollständig.