Warum haben Elementarteilchen keine Masse?

Dank E=mc² können Elementarteilchen keine Masse haben!

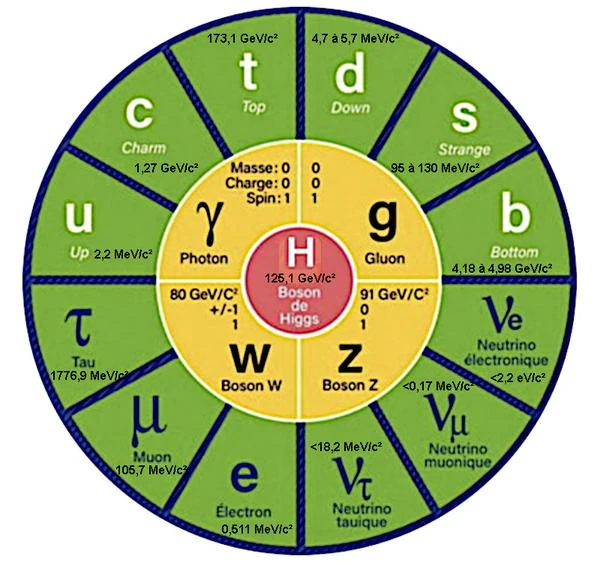
Die Welt der Elementarteilchen und ihrer Wechselwirkungen wird durch das sogenannte Standardmodell der Teilchenphysik beschrieben.
Im Standardmodell gelten einige Elementarteilchen wie Photonen und Gluonen als masselose Teilchen. Aber auch für andere Teilchen wie Quarks, W- und Z-Bosonen oder Leptonen messen wir eine Masse experimentell. Um die Ergebnisse besser vergleichbar zu machen, wird die Masse, die in Energie umgewandelt werden kann und umgekehrt, in Elektronenvolt gemessen.
Das Standardmodell gilt jedoch nur für Elementarteilchen, die keine intrinsische Masse haben, also keine ihrer Natur entsprechende Masse haben. Außerdem müssen sich diese Teilchen mit Lichtgeschwindigkeit bewegen.
Diese schöne Konstruktion der Physik konnte 2012 mit der Entdeckung des Higgs-Bosons aus dieser Sackgasse herauskommen.
Tatsächlich ist die Masse der Teilchen keine intrinsische Eigenschaft mehr, sondern ergibt sich aus ihrer Wechselwirkung mit dem Higgs-Feld. Je stärker die Wechselwirkung mit dem Higgs-Feld ist, desto größer ist die Trägheit, die ihnen das verleiht, was wir Masse nennen.

Die spezielle Relativitätstheorie von Albert Einstein (1879-1955) besagt, dass Energie und Masse äquivalent sind und durch die Gleichung E=mc zusammenhängen².
Das bedeutet, dass ein massiver Körper Energie hat, einfach weil er Masse hat, und diese Energie ist enorm, 1 Gramm Materie = 8,99 x 10¹² Joule (J).
Bei Teilchen stellt diese Energie die Masse eines ruhenden Teilchens dar. Wenn sich das Teilchen jedoch bewegt, muss diese Gleichung die kinetische Energie berücksichtigen.
E=mc² erschien erst 1912. Im Jahr 1905 wurde die Gesamtenergie wie folgt formuliert: E² = m²c⁴ + p²c². Wenn der Impuls (p) Null ist, sind die beiden Gleichungen identisch. Die Gleichung kann auch ausgedrückt werden als: E = √(m²c⁴ + p²c²)
Diese Gleichung E² = (pc)² + (mc²)² oder ihr Äquivalent E = √(m²c⁴ + p²c²) berücksichtigt die Massenenergie und die Bewegungsenergie des Teilchens.
Genau diese Formel ermöglicht die Existenz von Teilchen der Masse Null. Wenn sein Impuls tatsächlich ungleich Null ist, kann das Teilchen keine Masse und keine Energie haben. In diesem Fall können masselose Teilchen nicht ruhen, sie haben notwendigerweise eine Geschwindigkeit, nämlich die des Lichts.

Warum müssen sich masselose Teilchen mit Lichtgeschwindigkeit bewegen?

Wenn ein Körper stationär ist, beträgt seine Gesamtenergie E=mc². In diesem Fall messen wir die Trägheit eines Körpers (Trägheitsmasse) als seine Gesamtmasse. Das bedeutet, dass seine träge Masse = E/c² ist.
Wenn ein Körper in Bewegung ist, beträgt seine Gesamtenergie E = √(m²c⁴ + p²c²), also E = mc² + pc (seine kinetische Energie).
Somit ist für ein masseloses Teilchen E² = (mc²)² + (pc)² oder E = mc² + pc oder E = pc
In der Gleichung E = mc² + pc stellt pc die Bewegungsenergie eines Teilchens dar. p ist der Impuls des Teilchens, der gleich seiner Masse m multipliziert mit seiner Geschwindigkeit v ist, und c ist die Lichtgeschwindigkeit. Somit ist pc = mvc, wobei m die Masse des Teilchens und v seine Geschwindigkeit ist.
Für ein masseloses Teilchen E = c bedeutet dies, dass ein masseloses Teilchen nur eine Geschwindigkeit haben kann, nämlich die des Lichts.

Warum ist die Lichtgeschwindigkeit ein Tempolimit?

Trägheit ist die Energie, die benötigt wird, um einen ruhenden Körper in Bewegung zu versetzen oder bei der Bewegung seine Geschwindigkeit zu ändern. Tatsächlich gilt: Je massiver ein Körper ist, desto mehr widersteht er Bewegungsänderungen. Mit anderen Worten: Je massiver ein Objekt ist, desto schwieriger ist es, es zu beschleunigen oder abzubremsen, da die Trägheit mit der Geschwindigkeit zunimmt. Es kommt ein Moment, in dem die Trägheit so groß ist, dass wir eine Grenzgeschwindigkeit erreichen, die des Lichts.