Última actualización 04 de mayo de 2023

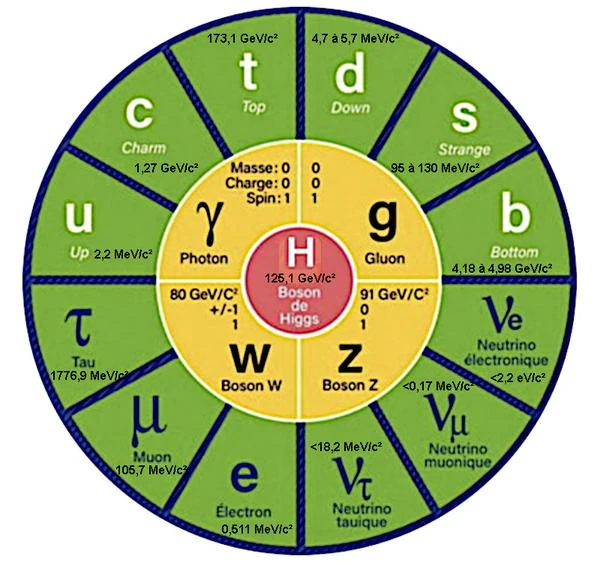
¿Por qué las partículas elementales no tienen masa?

¡Gracias a E=mc², las partículas elementales pueden no tener masa!

El mundo de las partículas elementales y sus interacciones está descrito por lo que se llama el Modelo Estándar de la física de partículas.
En el modelo estándar, algunas partículas elementales como fotones y gluones se consideran partículas sin masa. Pero para otras partículas como los quarks, los bosones W y Z o los leptones, la masa se mide experimentalmente. La masa, que se puede convertir en energía y viceversa, se mide en electronvoltios para que los resultados sean más fáciles de comparar.
Sin embargo, el modelo estándar solo se aplica a partículas elementales que no tienen masa intrínseca, es decir, no tienen masa específica a su naturaleza. Además, estas partículas deben moverse a la velocidad de la luz.
Esta hermosa construcción de la física pudo salir de este impasse en 2012 con el descubrimiento del bosón de Higgs.
De hecho, la masa de las partículas ya no es una propiedad intrínseca sino que proviene de su interacción con el campo de Higgs. Cuanto más fuerte es la interacción con el campo de Higgs, mayor es la inercia, lo que les da lo que llamamos masa.

La teoría especial de la relatividad de Albert Einstein (1879-1955) dice que la energía y la masa son equivalentes y están relacionadas por la ecuación E=mc².
Lo que significa que un cuerpo masivo tiene energía solo porque tiene masa y esta energía es enorme, 1 gramo de materia = 8,99 x 10¹² julios (J).
En lo que respecta a las partículas, esta energía representa la masa de una partícula en reposo. Sin embargo, cuando la partícula está en movimiento, esta ecuación debe tener en cuenta la energía cinética.
E=mc² solo apareció en 1912. En 1905, la energía total se formula de la siguiente manera E² = m²c⁴ + p²c², si el impulso (p) es nulo entonces las dos ecuaciones son idénticas. La ecuación también se puede expresar como: E = √(m²c⁴ + p²c²)
Esta ecuación E² = (pc)² + (mc²)², o su equivalente E = √(m²c⁴ + p²c²), tiene en cuenta la energía de masa y la energía de movimiento de la partícula.
Es precisamente esta fórmula la que hace posible la existencia de partículas de masa cero. De hecho, si su impulso es distinto de cero, entonces la partícula puede no tener masa y aún así tener energía. En este caso, las partículas sin masa no pueden estar en reposo, deben tener una velocidad, la de la luz.

¿Por qué las partículas sin masa tienen que moverse a la velocidad de la luz?

Si un cuerpo está estacionario, su energía total es E=mc². En este caso, medimos la inercia de un cuerpo (masa inercial) como su masa total. Lo que significa que su masa inercial = E/c².
Si un cuerpo está en movimiento, su energía total es E = √(m²c⁴ + p²c²), es decir, E = mc² + pc (su energía cinética).
Así, para una partícula sin masa E² = (mc²)² + (pc)² o E = mc² + pc o E = pc
En la ecuación E = mc² + pc, pc representa la energía de movimiento de una partícula. p es el momento de la partícula, que es igual a su masa m multiplicada por su velocidad v, y c es la velocidad de la luz. Así, pc = mvc, donde m es la masa de la partícula y v es su velocidad.
Para una partícula sin masa E = c, es por eso que una partícula sin masa solo puede tener una velocidad que la de la luz.

¿Por qué la velocidad de la luz es un límite de velocidad?

La inercia es la energía requerida para poner en movimiento un cuerpo estacionario o para cambiar su velocidad cuando está en movimiento. En efecto, cuanto más macizo es un cuerpo, más se resiste al cambio de movimiento. En otras palabras, cuanto más masivo es un objeto, más difícil es acelerarlo o disminuirlo porque la inercia aumenta con la velocidad. Llega un momento en que la inercia es tan grande que llegamos a un límite de velocidad, el de la luz.