Dernière mise à jour : 04 mai 2023

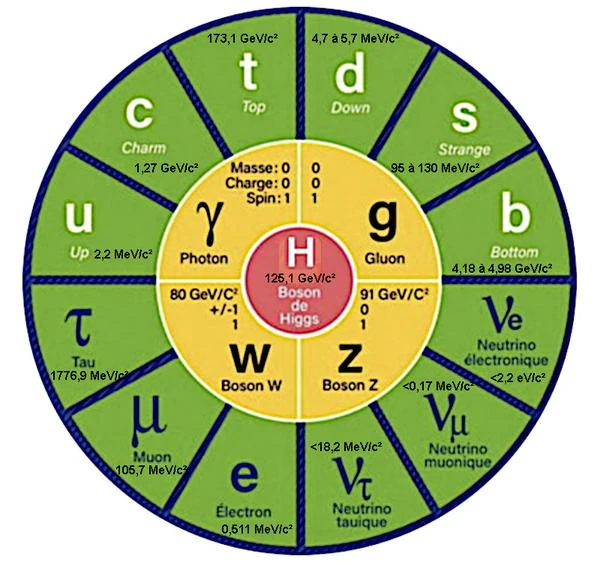
Pourquoi les particules élémentaires n'ont pas de masse ?

Grâce à E=mc², les particules élémentaires peuvent, ne pas avoir de masse !

Le monde des particules élémentaires ainsi que leurs interactions est décrit par ce qu'on appelle le Modèle Standard de la physique des particules.
Dans le modèle standard, certaines particules élémentaires comme les photons et les gluons sont considérées comme des particules sans masse. Mais pour les autres particules comme les quarks, les bosons W et Z ou les leptons, on mesure expérimentalement une masse. La masse, qui peut être convertie en énergie et vice versa, est mesurée en électronvolts afin de rendre les résultats plus facilement comparables.
Cependant le modèle standard ne s'applique qu'à des particules élémentaires qui n’ont pas de masse intrinsèque, c’est-à-dire qu’elles n’ont pas de masse propre à leur nature. De plus ces particules doivent se déplacer à la vitesse de la lumière.
Cette belle construction de la physique a pu sortir de cette impasse en 2012 avec la découverte du boson de Higgs.
En effet, la masse des particules n'est plus une propriété intrinsèque mais vient de leur interaction avec le champ de Higgs. Plus l'interaction avec le champ de Higgs est forte et plus l'inertie est grande ce qui leur donne ce que nous appelons une masse.

La théorie de la relativité restreinte d'Albert Einstein (1879-1955) dit que l'énergie et la masse sont équivalentes et sont liées par l'équation E=mc².
Ce qui signifie qu'un corps massif a de l'énergie du seul fait qu'il a une masse et cette énergie est énorme, 1 gramme de matière = 8,99 x 10¹² joules (J).
En ce qui concerne les particules, cette énergie représente la masse d'une particule au repos. Cependant, lorsque la particule est en mouvement, cette équation doit prendre en compte l'énergie cinétique.
E=mc² n'apparait qu'en 1912. En 1905, l'énergie totale est formulée de la façon suivante E² = m²c⁴ + p²c², si l'impulsion (p) est nulle alors les deux équations sont identiques. L'équation peut également être exprimée sous la forme suivante : E = √(m²c⁴ + p²c²)
Cette équation E² = (pc)² + (mc²)², ou son équivalent E = √(m²c⁴ + p²c²), tient compte de l'énergie de masse et de l'énergie de mouvement de la particule.
C'est justement cette formule qui rend possible l'existance de particules de masse nulle. En effet, si son impulsion est non nulle, alors la particule peut ne pas avoir de masse et avoir de l'énergie. Dans ce cas, les particules sans masse ne peuvent pas être au repos, elles ont obligatoirement une vitesse, celle de la lumière.

Pourquoi les particules sans masse doivent se déplacer à la vitesse de la lumière ?

Si un corps est immobile, son énergie totale est E=mc². Dans ce cas, on mesure l'inertie d'un corps (masse inertielle) comme étant sa masse totale. Ce qui veut dire que sa masse inertielle = E/c².
Si un corps est en mouvement, son énergie totale est E = √(m²c⁴ + p²c²), c'est à dire que E = mc² + pc (son énergie cinétique).
Ainsi, pour une particule sans masse E² = (mc²)² + (pc)² ou E = mc² + pc ou E = pc
Dans l'équation E = mc² + pc, pc représente l'énergie de mouvement d'une particule. p est la quantité de mouvement de la particule, qui est égale à sa masse m multipliée par sa vitesse v, et c est la vitesse de la lumière. Ainsi, pc = mvc, où m est la masse de la particule et v est sa vitesse.
Pour une particule sans masse E = c, c'est pourquoi une particule sans masse ne peut avoir qu'une seule vitesse celle de la lumière.

Pourquoi la vitesse de la lumière est une vitesse limite ?

L'inertie est l'énergie nécessaire pour mettre en mouvement un corps immobile ou pour modifier sa vitesse lorsqu'il est en mouvement. En effet plus un corps est massif et plus il résiste au changement de mouvement. Autrement dit, plus un objet est massif, plus il est difficile de l'accélérer ou de le ralentir car l'inertie augmente avec la vitesse. Il arrive un moment où l'inertie est si grande qu'on atteint une vitesse limite, celle de la lumière.