Imaginez un instant que dans l'atome, l'électron ne soit plus une petite planète tournant sagement autour d'un noyau-soleil, mais une note de musique, une vibration, une onde. C'est cela, la révolution conceptuelle déclenchée par Erwin Schrödinger (1887-1961) en 1926.
L'équation de Schrödinger ne nous dit pas où se trouve l'électron avec certitude, mais où il est susceptible de se trouver. Elle transforme l'espace atomique possible en une piste de danse où les figures du danseur dessinent les orbitales probables.
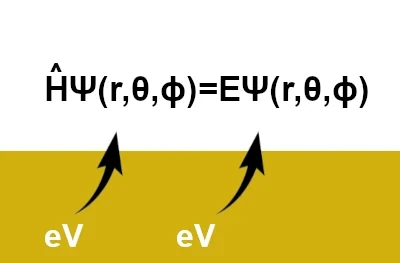
L'équation de Schrödinger s'écrit : \(\hat{H}\,\Psi(r,\theta,\phi)=E\,\Psi(r,\theta,\phi)\) où $(r, \theta, \phi)$ sont des coordonnées sphériques (r : La coordonnée radiale, θ : La coordonnée polaire, ϕ : La coordonnée azimutale). Cependant dans sa forme la plus simple, elle s'écrit : \( \hat{H} \Psi = E \Psi \)
Pour percer les mystères de l'atome, il faut une clé spéciale. Cette clé, c'est ce que les physiciens appellent la "fonction d'onde". On lui a donné un petit nom chic : Ψ (qui se lit "Psi", comme le début de "psyché" ou le trident de Neptune).
Imaginez que Ψ est une sorte de "carte de navigation" pour l'électron. Cette carte ne dit pas où va aller l'électron mais où il pourra aller. Plus exactement, elle décrit les endroits où vous avez des chances de le trouver, et les endroits où vous ne pourrez pas le trouver.
À gauche, \(\hat{H}\) représente "tout ce qui se passe dans l'atome" (l'attraction du noyau, l'énergie, les contraintes). À droite, \(E\) est le résultat : l'énergie que l'électron doit avoir pour être stable dans cette configuration.
Résoudre cette équation, c'est comme chercher la bonne note sur un piano pour qu'elle résonne parfaitement dans une pièce. On ne peut pas jouer n'importe quoi : seules certaines notes (les énergies \(E\)) et certaines manières de vibrer (les fonctions Ψ) fonctionnent harmonieusement.
Ce fut le grand dilemme des physiciens jusqu'à ce que Max Born (1882-1970) ait une intuition géniale. Il a dit : "Ne regardez pas Ψ elle-même, regardez son reflet, son carré, \(|\Psi|^2\)". C'est comme la fumée qui révèle un nuage de probabilité où l'objet était avant que le magicien le fasse disparaitre. Ainsi, \(|\Psi|^2\) nous indique, point par point dans l'espace autour du noyau, la probabilité de présence de l'électron.
En clair, là où \(|\Psi|^2\) est grand c'est le "jardin" de l'atome, là où l'électron passe son temps. Là où \(|\Psi|^2\) est nul, c'est un "désert", l'électron ne vient jamais. L'électron devient alors moins une bille qu'un nuage, une trainée de lumière, une danse floue et élégante autour du noyau appelée "orbitale".
Appliquée à l'atome d'hydrogène (un proton et un électron), l'équation de Schrödinger révèle une série de solutions, d'états quantiques, chacun caractérisé par trois nombres, souvent appelés nombres quantiques. Chaque solution correspond à une orbitale atomique, une forme géométrique tridimensionnelle spécifique qui est la "zone de danse" privilégiée de l'électron.
Là où Niels Bohr (1885-1962) voyait des électrons tournant sur des orbites circulaires bien rangées, comme des planètes autour du Soleil, l'équation de Schrödinger révèle un univers autrement plus riche et poétique. Les solutions dessinent dans l'espace des formes géométriques d'une élégante complexité.
Ces formes ne sont pas de simples fantaisies mathématiques. Elles sont la clé de voute de la chimie. La géométrie des orbitales détermine comment les atomes peuvent se lier entre eux pour former des molécules. La direction des orbitales p, par exemple, explique la forme angulaire de la molécule d'eau (H2O). La richesse des orbitales d est responsable des couleurs éclatantes des ions des métaux de transition. Ainsi, l'équation de Schrödinger, par ses solutions, est la grammaire cachée qui dicte la structure de toute la matière qui nous entoure.
N.B. :
L'image mentale du "nuage électronique" est plus juste que celle de la "particule en mouvement". Une orbitale est une carte de probabilité instantanée. Si vous preniez une photographie ultra-rapide de l'atome, vous verriez l'électron en un point ; en superposant des millions de ces photographies, vous verriez apparaitre la forme de l'orbitale, comme une trace de lumière laissée par un danseur sur une scène sombre.
L'équation de Kaya : L'équation qui complique notre décarbonation 
La vitesse indépassable dans l’Univers : quand l'énergie devient infinie 
L’emballement électromagnétique : Le secret de la Vitesse de la lumière 
Comprendre l'Effet Photoélectrique : La Lumière et les Électrons 
À quelle distance se trouve l’horizon ? 
Comment les Panneaux
Solaires Injectent-ils l'Électricité dans le Réseau ? 
Dynamique de la Quantité de Mouvement pour expliquer
la propulsion des fusées ou des méduses 
Comment l'énergie des électrons dicte les propriétés chimiques 
Le rôle clé du principe d'incertitude quantique : Aucune particule ne peut être immobile 
Énergie et puissance : Ne pas confondre, le temps fait toute la différence 
Pourquoi y a-t-il une limite au froid, mais pas au chaud ? 
La loi de la chute des corps de Galilée 
La Loi des gaz parfaits : Une équation, des milliers d'applications 
L'équation de Schrödinger a révolutionné notre vision de la matière 
La magie du théorème de Noether : Du principe de moindre action aux lois de conservation 
Rapport entre masse grave et masse inertielle et principe d'équivalence
Troisième Equation de la Physique : La quantité de mouvement pour comprendre les collisions 
La deuxième équation essentielle en physique : L'intuition d'une grandeur qui se conserve 
La première équation de la physique : Comment mathématiser la force 
La force électromagnétique ou force de Lorentz 
L'énergie solaire reçue varie en fonction de l'inclinaison 
Pourquoi le marbre est plus froid
que le bois ? 
Pourquoi
un photon, qui n'a pas de masse, a une énergie ? 
Formule de Bayes et Intelligences Artificielles 
Les sept constantes fondamentales
de la physique 
Quelle est la température ressentie dans l'espace interstellaire ?
Courbes de rayonnement du corps noir : la loi de Planck
Le principe d'équivalence, les effets gravitationnels sont indiscernables d'une
accélération 
E=mc2 : Les quatre concepts fondamentaux de l'univers revisités 
Comment peser le soleil ? 
Equation de la chute libre des corps (1604) 
Coulomb vs Newton : la mystérieuse similitude des forces de l'Univers 
Equation de Boltzmann sur l'entropie (1877) 
Les équations de la relativité restreinte (1905)
L'équation de la relativité générale (1915) 
Équations de la rotation planétaire : entre moment cinétique et équilibre gravitationnel
Équation de la vitesse orbitale d'une planète 
L'équation de Planck 
Comprendre l'équation de Schrödinger sans faire de maths 
Les trois lois de Newton : De la pomme qui tombe aux planètes qui tournent 
Les équations de Maxwell 
Equation de Dirac 
Conservation de l'énergie 
Equation de l'induction électromagnétique 
Pourquoi les particules élémentaires n'ont pas de masse ? 
Différences entre chaleur et température