Description de l'image : Le photon est représenté par une onde sinusoïdale, symbolisant sa nature d'onde électromagnétique. L'énergie du photon est proportionnelle à sa fréquence (E=hν). Le point rouge symbolise l'aspect particulaire du photon. Le photon, sur la sinusoïde, possède une quantité de mouvement (p = E/c = hν/c).
L'équation E=mc2, proposée par Albert Einstein (1879-1955), établit une relation entre la masse m et l'énergie E d'un objet, avec c représentant la vitesse de la lumière dans le vide.
Cette équation implique que la masse peut être convertie en énergie et vice versa. D'après l'équation E=mc², il peut sembler paradoxal qu'une particule sans masse (m=0) puisse avoir de l'énergie (E ≠ 0).
Un photon dont la masse m=0, possède une énergie E≠0 car l'équation E=mc2 s'applique spécifiquement à des particules au repos. En effet, la relation énergie-masse pour une particule est donnée par l'équation complète de la relativité restreinte : E2=(pc)2+(m0c2)2 où p est l'impulsion et m0 est la masse au repos.
Le photon est une particule sans masse et sans charge électrique. Il est le quantum du champ électromagnétique, ce qui signifie qu'il est une excitation élémentaire de ce champ. Sa description est gouvernée par l'équation de Maxwell et, au niveau quantique, par l'équation de Dirac pour les particules sans masse.
Un photon est donc défini par sa nature intrinsèque de porteur d'énergie quantique, caractérisée par sa fréquence et sa longueur d'onde. Étant donné que m0=0 pour un photon, s'il était au repos (v=0), cela impliquerait que son énergie E serait nulle (puisque p=0 à v=0). Or, l'existence d'un photon est indissociable de sa possession d'énergie. Un photon avec une énergie nulle n'aurait pas de sens physique et ne pourrait pas exister.
La théorie d'Einstein prédit qu'il existe une vitesse limite universelle, c, à laquelle aucune particule ayant une masse ne peut atteindre ni dépasser. Cette vitesse correspond à la vitesse de la lumière dans le vide. Ainsi, pour qu'un photon existe, il doit toujours se déplacer à la vitesse c.
Les photons sont donc des particules de lumière sans masse au repos (m0=0) qui se déplacent toujours à la vitesse de la lumière c. Ils possèdent une quantité de mouvement (p) et donc de l'énergie.
La relation entre l'énergie et la quantité de mouvement pour un photon est donnée par l'équation E=pc.
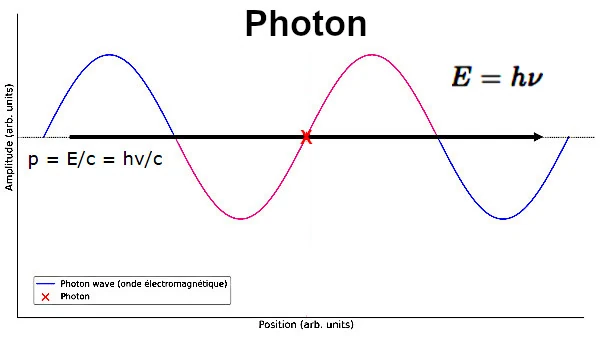
L'énergie d'un photon est donnée par l'équation de Planck E=hν où E est l'énergie, h est la constante de Planck (6.626×10^−34J, ν (nu) est la fréquence du photon.
Cette relation E=hν montre que l'énergie d'un photon est proportionnelle à sa fréquence.
En combinant la relation E=pc avec l'équation de Planck, nous obtenons p = E/c = hν/c
Dans le contexte relativiste, pour les particules massives en mouvement, l'énergie totale E est donnée par l'équation relativiste E2=(m0c2)2 + (pc)2.
Pour les photons, la masse au repos m est nulle, donc cette équation se simplifie à : E=pc.
En résumé, bien que les photons n'aient pas de masse au repos, ils possèdent de l'énergie et une quantité de mouvement. L'énergie d'un photon est liée à sa fréquence par l'équation E=hν, et sa quantité de mouvement est donnée par p=E/c. L'équation E=mc2 s'applique aux particules au repos, mais pour les photons le repos n'existe pas. Le photon est une excitation élémentaire du champ électromagnétique.
La deuxième équation essentielle en physique
La première équation essentielle en physique
La force électromagnétique ou force de Lorentz
L'énergie solaire reçue varie en fonction de l'inclinaison
Pourquoi le marbre est plus froid que le bois ?
Théorie du mur de Planck