¿Por qué un fotón que no tiene masa tiene energía?

Relación entre Masa y Energía

La ecuación E=mc², propuesta por Albert Einstein (1879-1955), establece una relación entre la masa m y la energía E de un objeto, con c representando la velocidad de la luz en el vacío.
Esta ecuación implica que la masa puede ser convertida en energía y viceversa. Según la ecuación E=mc², puede parecer paradójico que una partícula sin masa (m=0) pueda tener energía (E ≠ 0).
Un fotón con masa m=0 tiene energía E≠0 porque la ecuación E=mc² se aplica específicamente a partículas en reposo. De hecho, la relación energía-masa para una partícula está dada por la ecuación completa de la relatividad especial: E²=(pc)²+(m₀c²)² donde p es el impulso y m₀ es la masa en reposo.

Imposibilidad del Reposo para un Fotón

El fotón es una partícula sin masa y sin carga eléctrica. Es el cuanto del campo electromagnético, lo que significa que es una excitación elemental de este campo. Su descripción está gobernada por las ecuaciones de Maxwell y, a nivel cuántico, por la ecuación de Dirac para partículas sin masa.
Un fotón está definido por su naturaleza intrínseca como portador de energía cuántica, caracterizada por su frecuencia y longitud de onda. Dado que m₀=0 para un fotón, si estuviera en reposo (v=0), esto implicaría que su energía E sería nula (ya que p=0 a v=0). Sin embargo, la existencia de un fotón es inseparable de su posesión de energía. Un fotón con energía nula no tendría sentido físico y no podría existir.
La teoría de Einstein predice que existe un límite de velocidad universal, c, que ninguna partícula con masa puede alcanzar ni superar. Esta velocidad corresponde a la velocidad de la luz en el vacío. Por lo tanto, para que un fotón exista, debe moverse siempre a la velocidad c.

Energía y Fotones

Los fotones son, por lo tanto, partículas de luz sin masa en reposo (m₀=0) que siempre se mueven a la velocidad de la luz c. Poseen cantidad de movimiento (p) y, por lo tanto, energía.
La relación entre la energía y la cantidad de movimiento para un fotón está dada por la ecuación E=pc.
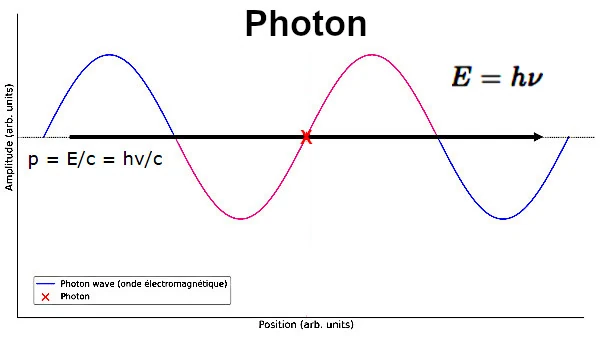
La energía de un fotón está dada por la ecuación de Planck E=hν donde E es la energía, h es la constante de Planck (6.626×10^−34J), ν (nu) es la frecuencia del fotón.
Esta relación E=hν muestra que la energía de un fotón es proporcional a su frecuencia.

Combinando la relación E=pc con la ecuación de Planck, obtenemos p = E/c = hν/c.

En el contexto relativista, para las partículas masivas en movimiento, la energía total E está dada por la ecuación relativista E²=(m₀c²)² + (pc)².
Para los fotones, la masa en reposo m es nula, por lo que esta ecuación se simplifica a: E=pc.

Conclusión

En resumen, aunque los fotones no tienen masa en reposo, poseen energía y cantidad de movimiento. La energía de un fotón está relacionada con su frecuencia por la ecuación E=hν, y su cantidad de movimiento está dada por p=E/c. La ecuación E=mc² se aplica a partículas en reposo, pero para los fotones el reposo no existe. El fotón es una excitación elemental del campo electromagnético.