La ecuación de Schrödinger revolucionó nuestra visión de la materia

De la certeza a la probabilidad: el átomo según Schrödinger

Imagina por un momento que en el átomo, el electrón ya no es un pequeño planeta que gira ordenadamente alrededor de un núcleo-sol, sino una nota musical, una vibración, una onda. Esta es la revolución conceptual desencadenada por Erwin Schrödinger (1887-1961) en 1926.

La ecuación de Schrödinger (ecuación fundamental de la mecánica cuántica que describe la evolución de una partícula mediante una función de onda.) no nos dice dónde está el electrón con certeza, sino dónde es probable que se encuentre. Transforma el espacio atómico posible en una pista de baile donde las figuras del bailarín dibujan los orbitales probables.

Entender la ecuación de Schrödinger sin complicarse

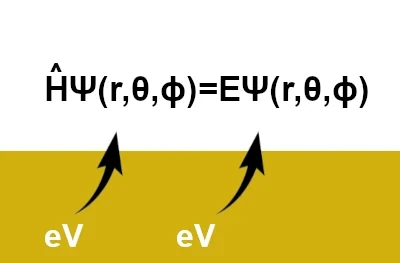
La ecuación de Schrödinger se escribe: \(\hat{H}\,\Psi(r,\theta,\phi)=E\,\Psi(r,\theta,\phi)\) donde \((r, \theta, \phi)\) son coordenadas esféricas (r: coordenada radial, θ: coordenada polar, ϕ: coordenada azimutal). Sin embargo, en su forma más simple, se escribe: \( \hat{H} \Psi = E \Psi \)

Para descifrar los misterios del átomo, se necesita una llave especial. Esta llave es lo que los físicos llaman la "función de onda". Le han dado un nombre elegante: Ψ (que se pronuncia "Psi", como el principio de "psique" o el tridente de Neptuno).

¿Cómo leer simplemente \( \hat{H} \Psi = E \Psi \)?

Imagina que Ψ es una especie de "mapa de navegación" para el electrón. Este mapa no dice adónde irá el electrón, sino adónde puede ir. Más exactamente, describe los lugares donde es probable encontrarlo y los lugares donde no lo encontrarás.

A la izquierda, \(\hat{H}\) representa "todo lo que sucede en el átomo" (la atracción del núcleo, la energía, las restricciones). A la derecha, \(E\) es el resultado: la energía que el electrón debe tener para ser estable en esta configuración.

Resolver esta ecuación es como buscar la nota correcta en un piano para que resuene perfectamente en una habitación. No se puede tocar cualquier cosa: solo ciertas notas (energías \(E\)) y ciertas formas de vibrar (funciones Ψ) funcionan armoniosamente.

¿Pero cómo es Ψ?

Este fue el gran dilema de los físicos hasta que Max Born (1882-1970) tuvo una intuición genial. Dijo: "No miren Ψ en sí misma, miren su reflejo, su cuadrado, \(|\Psi|^2\)". Es como el humo que revela una nube de probabilidad donde estaba el objeto antes de que el mago lo hiciera desaparecer. Así, \(|\Psi|^2\) nos indica, punto por punto en el espacio alrededor del núcleo, la probabilidad de presencia del electrón.

En resumen, donde \(|\Psi|^2\) es grande es el "jardín" del átomo, donde el electrón pasa su tiempo. Donde \(|\Psi|^2\) es cero, es un "desierto", el electrón nunca viene. El electrón se convierte entonces menos en una canica y más en una nube, un rastro de luz, una danza difusa y elegante alrededor del núcleo llamada "orbital".

Los patrones de la danza electrónica: los orbitales atómicos

Aplicada al átomo de hidrógeno (un protón y un electrón), la ecuación de Schrödinger revela una serie de soluciones, estados cuánticos, cada uno caracterizado por tres números, a menudo llamados números cuánticos. Cada solución corresponde a un orbital atómico, una forma geométrica tridimensional específica que es la "zona de baile" privilegiada del electrón.

Donde Niels Bohr (1885-1962) veía electrones girando en órbitas circulares ordenadas, como planetas alrededor del Sol, la ecuación de Schrödinger revela un universo mucho más rico y poético. Las soluciones dibujan en el espacio formas geométricas de elegante complejidad.

• La esfera perfecta (orbital s): La más simple de ellas, llamada 1s, es una esfera. El electrón no tiene dirección preferida; está presente de manera homogénea alrededor del núcleo, como una niebla perfectamente simétrica.
• Las mancuernas (orbitales p): Tan pronto como nos alejamos un poco del núcleo (segundo nivel de energía), el espacio se estructura. Aparecen entonces tres formas idénticas en "mancuerna", cada una apuntando en una dirección del espacio (según los ejes x, y y z). El electrón se concentra entonces en dos lóbulos opuestos, a ambos lados de una zona de silencio (el plano nodal).
• Las flores de la materia (orbitales d y f): A distancias aún mayores, la coreografía se enriquece. Los orbitales d adoptan geometrías que evocan tréboles de cuatro hojas. Los orbitales f, por su parte, despliegan pétalos múltiples en disposiciones aún más sofisticadas. Verdaderas firmas matemáticas del espacio, son para la química lo que las escalas son para la música: la estructura fundamental que permite todas las combinaciones, todas las moléculas, toda la materia que nos rodea.

Estas formas no son simples fantasías matemáticas. Son la piedra angular de la química. La geometría de los orbitales determina cómo los átomos pueden unirse entre sí para formar moléculas. La dirección de los orbitales p, por ejemplo, explica la forma angular de la molécula de agua (H₂O). La riqueza de los orbitales d es responsable de los colores brillantes de los iones de los metales de transición. Así, la ecuación de Schrödinger, a través de sus soluciones, es la gramática oculta que dicta la estructura de toda la materia que nos rodea.

N.B.:
La imagen mental de la "nube electrónica" es más precisa que la de la "partícula en movimiento". Un orbital es un mapa de probabilidad instantánea. Si tomaras una fotografía ultra rápida del átomo, verías el electrón en un punto; al superponer millones de estas fotografías, verías aparecer la forma del orbital, como un rastro de luz dejado por un bailarín en un escenario oscuro.