Imagen: El físico teórico británico Paul Dirac (1902-1984) en 1928 formuló esta ecuación sobre el comportamiento de las partículas de alta energía.
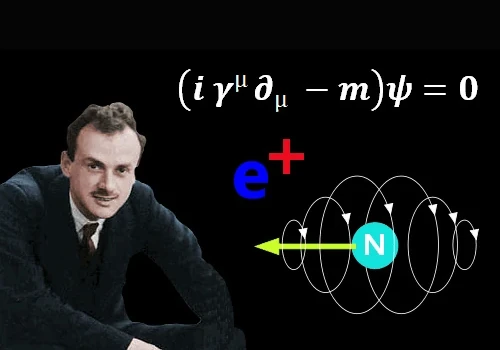
La ecuación de Dirac fue formulada por el físico teórico británico Paul Dirac (1902-1984) en 1928.
La ecuación de Dirac es importante en la física cuántica porque es capaz de describir el comportamiento de partículas de alta energía que se mueven a velocidades cercanas a la velocidad de la luz, como los electrones, que no pueden ser descritas con precisión por las ecuaciones de la física clásica. En esta ecuación, Dirac combina la mecánica cuántica y la teoría especial de la relatividad de Albert Einstein.
La ecuación de Dirac tuvo un impacto significativo en la física cuántica y condujo a muchos descubrimientos importantes, como la predicción de la existencia de antimateria.
Es más general que la ecuación de Schrödinger, que solo se aplica a partículas no relativistas.
También introdujo la noción de giro (momento angular intrínseco) de las partículas, que es una propiedad fundamental de las partículas subatómicas.
También ha permitido comprender fenómenos como la polarización del vacío, que es la creación espontánea de pares partícula-antipartícula a partir del vacío cuántico.
La ecuación de Dirac se escribe: (iγ^μ∂_μ-mc)ψ=0
• I es el
• γ^μ representa una matriz gamma que depende de un índice μ. Las matrices gamma son matrices de 4x4 dimensiones (cuatro dimensiones del espacio-tiempo) que se utilizan para representar las propiedades
• ∂_μ es el operador de derivada parcial con respecto a la coordenada espacio-temporal μ (∂/∂xμ) = (∂/∂t, ∂/∂x, ∂/∂y, ∂/∂z). Este operador de derivada parcial se utiliza para describir cómo un campo físico, como el campo electromagnético o el campo gravitatorio, varía en el espacio-tiempo teniendo en cuenta los efectos relativistas.
• m es la masa de la partícula.
• es la velocidad de la luz en el vacío.
• ψ es la función de onda que describe el estado cuántico de la partícula.
¿Para qué se usa la ecuación de Dirac?
• La ecuación de Dirac se utiliza en la teoría cuántica de campos para describir las interacciones entre partículas elementales, lo que la convierte en una herramienta matemática esencial para la física de partículas.
• El descubrimiento de la existencia de antipartículas, en particular la del positrón (antipartícula del electrón) permite su uso en imagenología médica.
En efecto, la tomografía por emisión de positrones consiste en inyectar al paciente un fármaco radiotrazador cuyo isótopo radiactivo es un emisor de radiación β+, es decir, un emisor de positrones. Estos positrones se aniquilan inmediatamente al contacto con los electrones de los tejidos circundantes y se generan dos fotones gamma. La detección de estos fotones permite localizar el lugar de su emisión y la concentración del trazador en cada punto de los órganos.
• Permite explicar la fina estructura de las líneas espectrales del hidrógeno. Estas líneas brillantes que aparecen en el espectro de emisión o absorción de un elemento químico son causadas por la transición de electrones entre diferentes niveles de energía en los átomos.
• Es útil en colisionadores de electrones y positrones que aceleran simultáneamente dos haces de partículas en direcciones opuestas, uno de electrones y el otro de positrones. Durante estas colisiones frontales de alta energía, los electrones y los positrones se aniquilan, liberando una energía considerable capaz de crear nuevas partículas.
La ecuación de Dirac inspiró otras ecuaciones, como la ecuación de Klein-Gordon, que describe partículas sin espín (bosones), como fotones. En conclusión, fue uno de los mayores avances en la física teórica del siglo XX y amplió nuestra comprensión del universo. es posible que los primeros humanos en llegar a Marte lo hagan a bordo de una nave espacial de positrones.
Teoría del muro de Planck