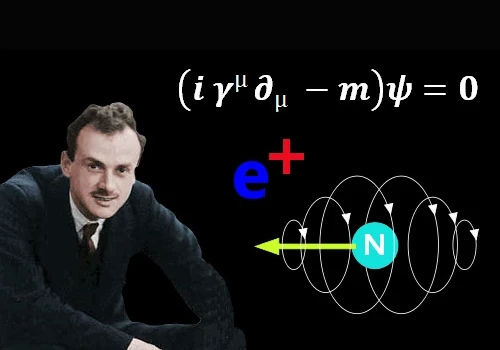
Image: British theoretical physicist Paul Dirac (1902-1984) in 1928 formulated this equation regarding the behavior of high energy particles.
The Dirac equation was formulated by the British theoretical physicist Paul Dirac (1902-1984) in 1928.
Dirac's equation is important in quantum physics because it is able to describe the behavior of high-energy particles that move at speeds close to the speed of light, such as electrons, which cannot be precisely described. by the equations of classical physics. In this equation, Dirac combines quantum mechanics and Albert Einstein's special theory of relativity.
Dirac's equation had a significant impact on quantum physics and led to many important discoveries, such as the prediction of the existence of antimatter.
It is more general than Schrödinger's equation, which only applies to non-relativistic particles.
She also introduced the notion of spin (intrinsic angular momentum) of particles, which is a fundamental property of subatomic particles.
It has also made it possible to understand phenomena such as vacuum polarization, which is the spontaneous creation of particle-antiparticle pairs from the quantum vacuum.
The Dirac equation is written: (iγ^μ∂_μ-mc)ψ=0
• I is the
• γ^μ represents a gamma matrix which depends on an index μ. Gamma matrices are 4x4 dimensional (four spacetime dimensions) matrices that are used to represent the
• ∂_μ is the partial derivative operator with respect to the space-time coordinate μ (∂/∂xμ) = (∂/∂t, ∂/∂x, ∂/∂y, ∂/∂z). This partial derivative operator is used to describe how a physical field, such as the electromagnetic field or the gravitational field, varies in space-time taking into account relativistic effects.
• m is the mass of the particle.
• is the speed of light in vacuum.
• ψ is the wave function that describes the quantum state of the particle.
What is the Dirac equation used for?
• Dirac's equation is used in quantum field theory to describe the interactions between elementary particles, making it an essential mathematical tool for particle physics.
• The discovery of the existence of antiparticles, in particular that of the positron (antiparticle of the electron) allows its use in medical imaging.
Indeed, positron emission tomography consists of injecting the patient with a radiotracer drug whose radioactive isotope is a β+ radiation emitter, that is to say a positron emitter. These positrons are immediately annihilated on contact with the electrons of the surrounding tissues, and two gamma photons are generated. The detection of these photons makes it possible to locate the place of their emission and the concentration of the tracer at each point of the organs.
• It makes it possible to explain the fine structure of the spectral lines of hydrogen. These bright lines that appear in the emission or absorption spectrum of a chemical element are caused by the transition of electrons between different energy levels in atoms.
• It is useful in electron-positron colliders which simultaneously accelerate two particle beams in opposite directions, one of electrons, the other of positrons. During these high-energy head-on collisions, the electrons and positrons annihilate, releasing considerable energy capable of creating new particles.
Dirac's equation inspired other equations, such as the Klein-Gordon equation, which describes spinless particles (bosons), like photons. In conclusion, it was one of the major developments in 20th century theoretical physics and expanded our understanding of the universe. it is possible that the first humans to reach Mars will do so aboard a positron spacecraft.
Relationship between gravitational mass and inertial mass and the equivalence principle 
The Third Essential Equation in Physics 
The Second Essential Equation in Physics 
The first essential equation in physics 
The electromagnetic force or Lorentz force 
The solar energy received depends on the angle of incidence 
Why is marble colder than wood? 
Planck's wall theory