Quantum Uncertainty: The Key Role of Heisenberg's Principle

Description of the image: Heisenberg's Uncertainty Principle is a cornerstone of quantum mechanics. It states that it is impossible to simultaneously and precisely know both the position and the momentum (or impulse) (\(\vec{p} = m \cdot \vec{v}\)) of a particle. Image source: astronoo.com

Heisenberg's Formula

The formula by Werner Heisenberg (1901-1976) is a fundamental discovery in quantum mechanics. Formulated in 1927, it expresses a fundamental limit on the precision with which certain pairs of physical properties, such as position (x) and momentum (p), can be known simultaneously.

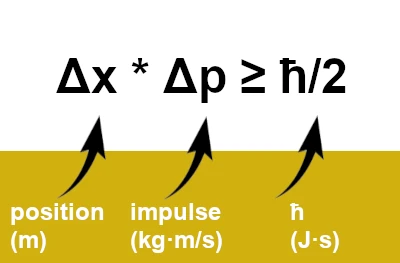
Heisenberg showed that the more precisely the position of a particle is measured, the less precisely its momentum can be known, and vice versa. This relationship is expressed mathematically by the inequality: Δx * Δp ≥ ħ/2, where \(\hbar = \frac{h}{2\pi}\) (h = Planck's constant and ħ = reduced Planck's constant).

Interpretation of the Terms

\(\Delta x\): uncertainty in the position of the particle.

\(\Delta p\): uncertainty in the momentum \(p = m v\), with \(m\) being the mass and \(v\) the velocity.

\(\hbar \approx 1.054 \times 10^{-34}\, \text{J.s}\) is the reduced Planck's constant.

The inequality means that the product of these two uncertainties can never be smaller than a limit given by \(\frac{\hbar}{2}\).

In other words, if you reduce the uncertainty in the position \(\Delta x\) of a particle, the uncertainty in its momentum \(\Delta p\) increases, and vice versa.

N.B.:
The position in meters of a quantum particle is explained by the absence of specific coordinates for a particle that is localized in a certain region of space, but its exact location at any given moment is described probabilistically, due to Heisenberg's uncertainty principle.

Example to Visualize the Idea of Heisenberg's Uncertainty Principle

Imagine you're trying to take a very sharp photo of a car speeding by. To get a sharp image, you need to use a very short exposure time. However, a short exposure time means less light is captured, which may result in a dark or blurry image if the light is insufficient.

• Precise position (sharp photo): If you manage to get a very sharp photo of the car, you’ve captured its position at a specific moment. However, due to the short exposure time, you have less information about its motion (speed), as you only see a snapshot without the context of movement.
• Precise motion (blurry photo): If you use a longer exposure time to capture more light and get a brighter image, the car will appear blurry due to its motion during the exposure. You now have more information about the motion (you see the blur indicating direction and speed), but you lose precision about the car's exact position at a given moment.

Impacts on Modern Physics

• Reality at the quantum scale: The uncertainty principle helped predict with accuracy the evolution of systems. This principle shows that reality at the quantum scale is intrinsically probabilistic. It replaced the deterministic view of classical physics with a probabilistic framework.
• Wave function collapse: The uncertainty implies that measuring a quantity can disturb the system, making the notion of an "objective observer" problematic. The concept of "wave function collapse", which posits that a measurement causes the wave function of a system to collapse into a definite state, emerged partly as a consequence of the uncertainty principle.
• Energy quantization: The uncertainty principle is crucial to explain phenomena like energy quantization in systems such as atoms (Bohr model) and molecules. Quantum effects influence macroscopic phenomena such as superconductivity and superfluidity.
• Tunneling effect: The uncertainty principle is also fundamental to explain the tunneling effect, a quantum phenomenon where a particle has a non-zero probability of crossing an energy barrier even if it doesn't have enough energy to surpass it according to classical physics laws. This phenomenon is used in devices such as tunnel effect transistors and scanning tunneling microscopes.
• Quantum vacuum: Due to the uncertainty, even a quantum vacuum (the ground state of a system) is not completely "empty" but subject to quantum fluctuations.
• Wave-particle duality: The uncertainty is closely related to wave-particle duality, which describes how quantum objects (such as electrons or photons) can behave as both waves and particles simultaneously. The uncertainty in position and momentum is a direct manifestation of this duality.