Description of the image: The law of conservation of momentum states that in an isolated system, that is, a system without external forces, the total momentum remains constant.
The third fundamental equation in classical physics, which could be considered essential, is the conservation of momentum equation or impulse conservation.
In other words, the sum of the momenta of objects before an event (such as a collision) is equal to the sum of the momenta after the event, provided no external force acts.
This law is particularly useful in studying collisions (elastic and inelastic) and explosions. For example, if two objects collide, the conservation of momentum allows calculating the final velocities of the objects after impact, provided their masses and initial velocities are known.
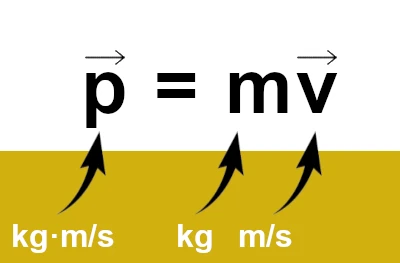
p = mv
• p is the momentum or impulse of the object, expressed in kilogram meters per second (kg·m/s),
• m is the mass of the object, in kilograms (kg),
• v is the velocity of the object, in meters per second (m/s).
Consider two objects with masses m1 and m2 moving with initial velocities v1 and v2. After the collision, their velocities are v'1 and v'2.
The conservation of momentum tells us: m1 v1 + m2 v2 = m1 v'1 + m2 v'2
The total kinetic energy of the system is conserved before and after the collision.
This equation, combined with kinetic energy if the collision is elastic, allows determining the velocities of the two objects after impact.
Velocity is a vector quantity because it describes not only how fast an object moves but also the direction in which it moves. This is essential for describing an object's complete movement in three-dimensional space.
Since velocity ($ \vec{v} $) is a vector quantity, momentum ($ \vec{p} $) must also be a vector. The direction and magnitude of p are determined by those of v.
Collisions are interactions where two or more objects come into contact and exchange energy and momentum. There are mainly two types of collisions based on the conservation of kinetic energy: elastic collisions and inelastic collisions.
In an elastic collision, the total kinetic energy of the system is conserved before and after the collision. This means the total kinetic energy of the objects involved in the collision remains constant, though energy may be redistributed among the objects as different movements and velocities.
Examples: Collisions between billiard balls or collisions between particles in a gas.
In an inelastic collision, the total kinetic energy is not conserved. Some of the kinetic energy is converted into other forms of energy, such as thermal energy, sound energy, or deformation energy. The objects may deform, heat up, or produce noise.
Examples: Collision between vehicles in a car accident where the cars deform and heat up, or the impact of a tennis ball against a wall where the ball changes shape.
The Second Essential Equation in Physics
The first essential equation in physics
The electromagnetic force or Lorentz force
The solar energy received depends on the angle of incidence
Why is marble colder than wood?
Planck's wall theory