The Planck Equation

N.B.: Joule-seconds (Js) are units of action and angular momentum that represent masses (in kg) multiplied by velocity (in m/s) multiplied by position.

E = hf

The Planck equation (1900), named after the German physicist Max Planck (1858-1947), is a formula that describes the relationship between the energy of a photon and the corresponding light frequency.

This equation was developed by the physicist to explain the spectral distribution of the radiation of the black body, which was a mystery at the time.

N.B.: In physics, a black body is an ideal object that completely absorbs all incident electromagnetic radiation, regardless of frequency or direction. It does not reflect or transmit any light, but it can emit radiation when heated, known as black body radiation.

When physicists calculated the spectral density of the energy radiated by a black body at a given temperature with the classical theory of electromagnetism, they did not obtain the actual energy distribution observed for black bodies.

The classical theory of electromagnetism assumed that energy was continuous, i.e., electromagnetic waves could have any energy. To solve this mystery, Planck hypothesized that energy is not exchanged continuously but in small discrete "packets" which he called "quanta". This hypothesis meant that electromagnetic energy could not take any value, but only multiples of a certain base energy equal to the frequency multiplied by a constant.

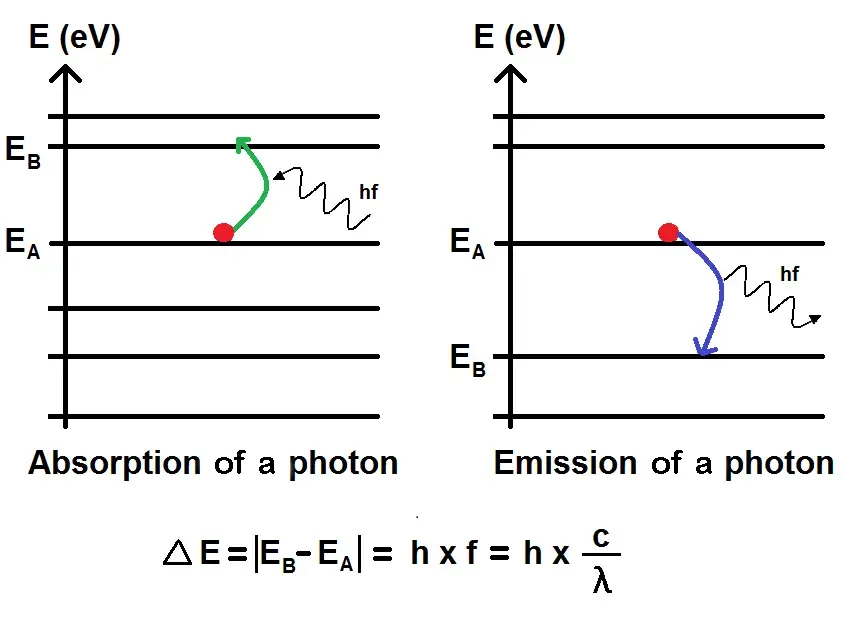
The equation is today one of the cornerstones of quantum physics and is expressed in the following form: E = hf where E represents the energy of the photon, f the frequency of the light, and h the Planck constant which has a value of 6.626 x 10^-34 joule-seconds.

This means that the energy E of an electromagnetic photon is directly proportional to its frequency ν, and the constant of proportionality is the Planck constant h. This relationship is today known as the Planck-Einstein equation.

What is E = hf used for?

The Planck equation had important implications for understanding the nature of light, which was considered at the time to be only an electromagnetic wave.

The Planck equation led to the development of quantum mechanics, which is the branch of physics that studies the properties and behavior of subatomic particles.

The Planck constant h, which relates the energy of photons to their frequency, is a fundamental constant of quantum physics because it serves to quantify the energy associated with electromagnetic interactions and all quantum processes. It plays an important role in understanding many phenomena such as wave-particle duality, photon emission and absorption, quantum transition energies in atoms and molecules, electrical conductivity of solids, electromagnetic radiation production in particle accelerators, understanding star formation, etc.

The Planck constant is used in many technological fields, notably for the study of spectroscopy, the design of semiconductors, the production of lasers, the design of solar cells, etc. It has invaded many equations of quantum physics, notably the Schrödinger equation, which describes the temporal evolution of the quantum states of a system. But also the Heisenberg uncertainty principle, which states that there is a fundamental limit to the precision with which the position and momentum of a particle can be simultaneously measured.