How Do Solar Panels Inject Electricity into the Grid?

Fundamental Concept: Current and Potential Difference

A Photovoltaic Panel connected to the domestic installation (and to the supplier network) produces a direct current (DC) voltage, which is then converted into a synchronized alternating current (AC) voltage by an inverter. This voltage is matched to the same frequency (50 Hz) and a comparable amplitude to that of the grid.

In electricity, current flows if and only if there is a potential difference (ΔV) — particularly in direct current, where only the instantaneous voltage difference determines the current flow. In contrast, in the case of two synchronized alternating sources (same frequency, same waveform), current can flow even if the instantaneous voltages are equal at times, thanks to a phase shift (a few degrees) between the sine waves.

In this context, it is the phase difference between the voltages, as well as the impedance characteristics of the circuit, that determine the existence and direction of the current.

N.B.: In a 220 V alternating voltage, the voltage varies from +311 V to -311 V. Indeed, the value of 220 V is the effective value (RMS) of the alternating voltage. This is the value used for power calculations and electrical equipment specifications. The alternating voltage oscillates between a maximum positive value and a maximum negative value. The maximum value (amplitude) is actually \( V_{\mathrm{CREST}} = V_{\mathrm{RMS}} \times \sqrt{2} \) → \( 220 \times \sqrt{2} \approx 311\,\text{V} \)

Role of Phase Shift in Energy Transfer

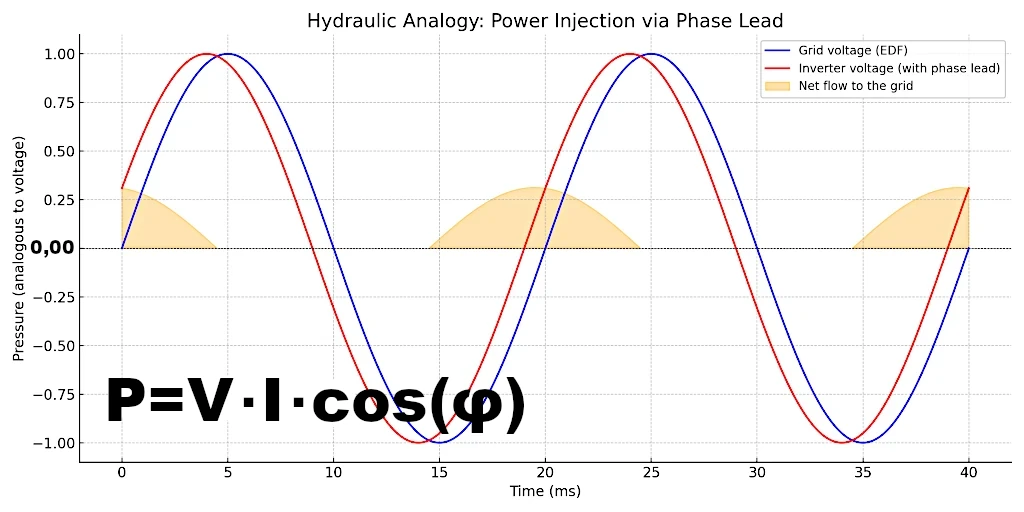
In terms of physics, this transfer obeys the power equation: \( P = V \cdot I \cdot \cos(\varphi) \). This formula is known as the "Active Power Formula in Single-Phase Sinusoidal Alternating Current."

• P is the active power (in watts, W),
• V is the effective voltage (in volts, V),
• I is the effective current (in amperes, A),
• cos(φ) is the power factor where φ is the phase shift between voltage and current.

Even if the effective voltage is nominally the same (230 V for example), it is the instantaneous voltage variations (phasing, dynamics, micro-adjustments) that allow the inverter to inject a directed current towards the grid.

Analogy with Two Variable Pressure Water Pipes

Imagine two hydraulic pumps connected to the two ends of the same pipe, each producing a pressure variation at a frequency of 50 Hz.

These variations create pressure waves in the fluid (similar to sound waves) that travel through the pipe. These waves cause areas of compression and relaxation of the fluid, without overall mass displacement, but with local oscillations of water particles.

This system is a good analogy for two alternating voltage sources in an electrical circuit: the pressure represents the voltage, the flow corresponds to the current, and the resistance to flow is similar to electrical impedance.

Case 1: 0° Phase Shift (pumps perfectly in phase)

The two pressures are identical at every moment.

There is no pressure difference between the two ends of the common pipe.

Therefore: zero flow at all times, no fluid movement.

• \( Q(t) = 0 \)
• \( \Delta p(t) = 0 \)
• Instantaneous power: \( P(t) = \Delta p(t) \cdot Q(t) = 0 \)
• Average power: 0

Conclusion: No energy transfer. The fluid is static despite the oscillating pressure.

Case 2: 180° Phase Shift (pumps in opposite phase)

Opposing pressures: when one pushes, the other pulls.

Maximum pressure difference at every moment.

The fluid oscillates strongly from one pump to the other, alternately.

The flow \( Q(t) \) is in opposite phase with the pressure difference.

The product \( \Delta p(t) \cdot Q(t) \) is negative half the time, positive the other half, but perfectly symmetrical.

Conclusion:

• Instantaneous power: variable, sometimes positive, sometimes negative.
• Average power: zero — there is cyclic energy exchange (like a capacitor or a coil), but no net transfer.
• Energy stored and released alternately.

Case 3: 90° Phase Shift (pumps in quadrature phase)

When one pump is at its maximum pressure, the other is at the point of maximum flow (because the pressure gradient is changing).

Pressure and flow are in quadrature (90° shift).

This corresponds to a situation where the instantaneous power is always non-zero, but changes sign during the cycle.

Conclusion:

• Instantaneous power: sinusoidal, with alternation between injection and absorption.
• Average power: always zero — as with 180°, there is an alternating energy transfer, without net accumulation.

Case 4: Intermediate Phase Shift (e.g., 5°)

In this case, the phase shift is neither totally zero (as in the 0° case), nor 90° (where pressure and flow are maximally shifted but without net transfer), nor maximal (as in the 180° case), but intermediate.

The pressure difference is not maximal at all times, but it varies partially.

The flow is also sinusoidal, but it is partially in phase with the pressure.

This phase shift creates a net energy transfer between the pumps, resulting in a real flow of fluid from one pump to the other.

• If pump A is ahead in phase of pump B, then energy is transferred from A to B, and the fluid moves on average from A to B.
• If pump A is behind in phase, then B transfers energy to A, and the fluid moves from B to A.

Current Injection Based on Phase Shift

Although an alternating instantaneous flow exists in all cases, a net mass transfer only occurs if the phase shift is partial (different from 0°, 90°, or 180°).

The fluid is therefore the medium of mechanical energy, and can become a vector of material transport in situations of net energy transfer.