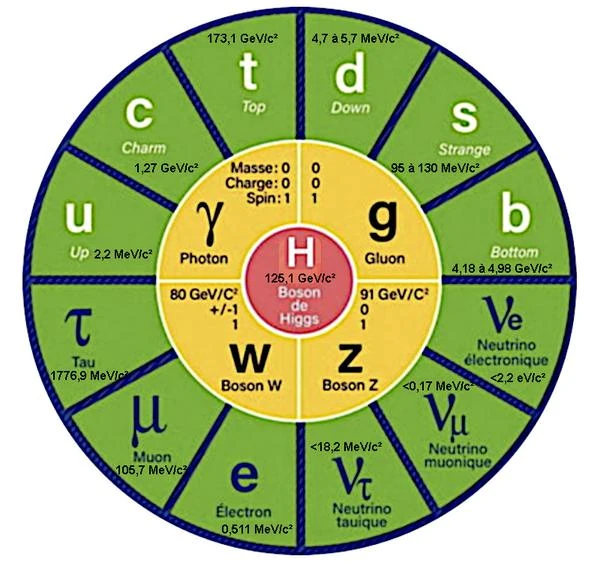
Image: Standard Model of particle physics.
The masses of the elementary particles: fermions (green boxes), mediator bosons (yellow boxes) and Higgs boson (red box).
Gauge bosons like photons and gluons have zero mass, while all other particles have masses, even the Higgs boson which gives particles their mass, has a mass of about 125.1 GeV/c².
The world of elementary particles and their interactions is described by what is called the Standard Model of particle physics.
In the standard model, some elementary particles like photons and gluons are considered massless particles. But for other particles such as quarks, W and Z bosons or leptons, a mass is experimentally measured. Mass, which can be converted into energy and vice versa, is measured in electron volts to make results more easily comparable.
However, the standard model only applies to elementary particles which have no intrinsic mass, i.e. they have no mass specific to their nature. Moreover, these particles must move at the speed of light.
This beautiful construction of physics was able to get out of this impasse in 2012 with the discovery of the Higgs boson.
Indeed, the mass of the particles is no longer an intrinsic property but comes from their interaction with the Higgs field. The stronger the interaction with the Higgs field, the greater the inertia, which gives them what we call mass.
Albert Einstein's (1879-1955) special theory of relativity says that energy and mass are equivalent and are related by the equation E=mc2.
Which means that a massive body has energy just because it has mass and this energy is enormous, 1 gram of matter = 8.99 x 10¹² joules (J).
As far as particles are concerned, this energy represents the mass of a particle at rest. However, when the particle is in motion, this equation must take into account the kinetic energy.
E=mc² only appeared in 1912. In 1905, the total energy is formulated as follows E² = m²c⁴ + p²c², if the impulse (p) is null then the two equations are identical. The equation can also be expressed as: E = √(m²c⁴ + p²c²)
This equation E² = (pc)² + (mc²)², or its equivalent E = √(m²c⁴ + p²c²), takes into account the mass energy and the energy of motion of the particle.
It is precisely this formula which makes possible the existence of particles of zero mass. Indeed, if its momentum is non-zero, then the particle may have no mass and still have energy. In this case, the massless particles cannot be at rest, they must have a speed, that of light.
If a body is stationary, its total energy is E=mc². In this case, we measure the inertia of a body (inertial mass) as being its total mass. Which means that its inertial mass = E/c².
If a body is in motion, its total energy is E = √(m²c⁴ + p²c²), ie E = mc² + pc (its kinetic energy).
Thus, for a massless particle E² = (mc²)² + (pc)² or E = mc² + pc or E = pc
In the equation E = mc² + pc, pc represents the motion energy of a particle. p is the momentum of the particle, which is equal to its mass m multiplied by its speed v, and c is the speed of light. Thus, pc = mvc, where m is the mass of the particle and v is its velocity.
For a massless particle E = c, this is why a massless particle can only have one speed that of light.
Inertia is the energy required to set a stationary body in motion or to change its speed when it is in motion. Indeed, the more a body is massive, the more it resists the change of movement. In other words, the more massive an object, the more difficult it is to speed it up or slow it down because inertia increases with speed. There comes a time when the inertia is so great that we reach a speed limit, that of light.